Декартово дерево — различия между версиями
(→Ссылки) |
(→Высота декартового дерева) |
||
| Строка 86: | Строка 86: | ||
== Высота декартового дерева == | == Высота декартового дерева == | ||
Мы уже выяснили, что сложность операций с декартовым деревом линейно зависит от его высоты. В действительности высота декартова дерева может быть линейной относительно его размеров. Например, высота декартова дерева, построенного по набору ключей <tex>(1, 1), \ldots, (n, n)</tex>, будет равна <tex>n</tex>. Во избежание таких случаев, полезным оказывается выбирать приоритеты в ключах случайно. | Мы уже выяснили, что сложность операций с декартовым деревом линейно зависит от его высоты. В действительности высота декартова дерева может быть линейной относительно его размеров. Например, высота декартова дерева, построенного по набору ключей <tex>(1, 1), \ldots, (n, n)</tex>, будет равна <tex>n</tex>. Во избежание таких случаев, полезным оказывается выбирать приоритеты в ключах случайно. | ||
| + | |||
| + | {{Теорема | ||
| + | |statement = Декартово дерево из <tex>n</tex> узлов, ключи <tex>y</tex> которых являются незавимыми непрерывными случайными величинами с одинаковым вероятностным распределением, имеет высоту <tex>O(\log n)</tex>. | ||
| + | |proof= | ||
| + | Замечание: В следующих утверждениях мы будем считать, что <tex>x_1 < x_2 < \ldots x_n</tex>, а каждое <tex>y_i</tex> выбрано случайно и независимо с одинаковым распределением, а также будем называть <tex>i</tex>-м узлом узел с ключом <tex>x_i</tex>. | ||
| + | |||
| + | {{Лемма | ||
| + | |statement = <tex>i</tex>-й узел является прародителем <tex>k</tex>-го узла тогда и только, когда <tex>y_i < y_j</tex> для любого <tex>j</tex> такого, что <tex>i < j \leqslant k</tex> или <tex>k \leqslant j < i</tex>. | ||
| + | |proof= | ||
| + | Рассмотрим случай <tex>i < k</tex>, в случае <tex>i > k</tex> доказательство аналогично. | ||
| + | |||
| + | Необходимость. Допустим, что <tex>y_i < y_j</tex> для всех <tex>i < j \leqslant k</tex>. Тогда по свойствам кучи <tex>i</tex>-й узел не может лежать в поддереве с корнем в <tex>k</tex>-м узле. Более того, не может существовать индекс <tex>j</tex> такой, что <tex>j</tex>-й узел общий прародитель <tex>i</tex>-го и <tex>k</tex>-го узлов, но эти узлы лежат в его разных поддеревьях. Если он существует, то <tex>x_i < x_j < x_k</tex>, следовательно, <tex>i < j < k</tex>. Но тогда <tex>j</tex>-й не мог быть прародителем <tex>i</tex>-го узла (опять же по свойствам кучи). Остался последний вариант взаимного расположения <tex>i</tex>-го и <tex>k</tex>-го узлов: <tex>i</tex>-й является прародителем <tex>k</tex>-го узла. | ||
| + | |||
| + | Достаточность. Пусть <tex>i</tex>-й узел является предком <tex>k</tex>-го узла. Докажем от противного. Предположим, что существует <tex>j</tex> такое, что <tex>i < j \leqslant k</tex> и <tex>y_j < y_i</tex>. По свойствам кучи <tex>i</tex>-й узел не может быть прародителем <tex>j</tex>-го узла. Если <tex>j</tex>-й узел является прародителем <tex>i</tex>-го узла, то из неравенства <tex>x_i < x_j < x_k</tex> следует, что <tex>i</tex>-й узел содержится в левом поддереве <tex>j</tex>-го узла, а <tex>k</tex>-й в правом. Это противоречит тому, что <tex>i</tex>-й узел прародитель <tex>k</tex>-го узла. Остается последний вариант взаимного расположения <tex>i</tex>-го и <tex>j</tex>-го узла: некоторый <tex>l</tex>-й узел является их общим прародителям, но они содержатся в его разных поддеревьях. Тогда получаем неравенство <tex>x_i < x_l < x_j \leqslant x_k</tex>, из которого следует, что <tex>k</tex>-й узел содержится в правом поддереве <tex>l</tex>-го узла. Снова противоречие. Значит, наше предположение не верно. | ||
| + | }} | ||
| + | |||
| + | |||
| + | }} | ||
== Ссылки == | == Ссылки == | ||
Версия 01:06, 12 апреля 2012
Эта статья про Курево
Содержание
Описание
Декартово дерево — это структура данных, объединяющая в себе бинарное дерево поиска и бинарную кучу (отсюда и второе её название: treap (tree + heap) и дерамида (дерево + пирамида), так же существует название курево (куча + дерево).
Более строго, это структура данных, которая хранит пары в виде бинарного дерева таким образом, что она является бинарным деревом поиска по и бинарной пирамидой по . Предполагая, что все и все являются различными, получаем, что если некоторый элемент дерева содержит , то у всех элементов в левом поддереве , у всех элементов в правом поддереве , а также и в левом, и в правом поддереве имеем: .
Дерамиды были предложены Сиделем (Siedel) и Арагоном (Aragon) в 1996 г.
Операции в декартовом дереве
Split
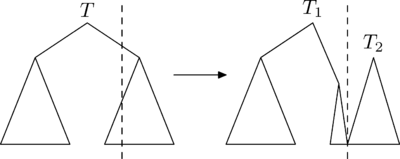
Операция (разрезать) позволяет сделать следующее: разрезать декартово дерево по ключу и получить два других декартовых дерева: и , причем в находятся все ключи дерева , не большие , а в — большие .
.
Эта операция устроена следующим образом.
Рассмотрим случай, в котором требуется разрезать дерево по ключу, большему ключа корня. Посмотрим, как будут устроены результирующие деревья и :
- : левое поддерево совпадёт с левым поддеревом . Для нахождения правого поддерева , нужно разрезать правое поддерево на и по ключу и взять .
- совпадёт с .
Случай, в котором требуется разрезать дерево по ключу, меньше либо равному ключа в корне, рассматривается симметрично.
Оценим время работы операции . Во время выполнения вызывается одна операция для дерева хотя бы на один меньшей высоты и делается ещё операция. Тогда итоговая трудоёмкость этой операции равна , где — высота дерева.
Merge
Рассмотрим вторую операцию с декартовыми деревьями — (слить).
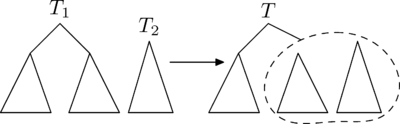
С помощью этой операции можно слить два декартовых дерева в одно. Причем, все ключи в первом(левом) дереве должны быть меньше, чем ключи во втором(правом). В результате получается дерево, в котором есть все ключи из первого и второго деревьев.
Рассмотрим принцип работы этой операции. Пусть нужно слить деревья и . Тогда, очевидно, у результирующего дерева есть корень. Корнем станет вершина из или с наибольшим ключом . Но вершина с самым большим из всех вершин деревьев и может быть только либо корнем , либо корнем . Рассмотрим случай, в котором корень имеет больший , чем корень . Случай, в котором корень имеет больший , чем корень , симметричен этому.
Если корня больше корня , то он и будет являться корнем. Тогда левое поддерево совпадёт с левым поддеревом . Справа же нужно подвесить объединение правого поддерева и дерева .
Рассуждая аналогично операции приходим к выводу, что трудоёмкость операции равна , где — высота дерева.
Insert
Операция добавляет в дерево элемент , где — ключ, а — приоритет.
- Реализация №1
- Разобьём наше дерево по ключу, который мы хотим добавить, то есть .
- Сливаем первое дерево с новым элементом, то есть .
- Сливаем получившиеся дерево со вторым, то есть .
- Реализация №2
- Сначала спускаемся по дереву (как в обычном бинарном дереве поиска по ), но останавливаемся на первом элементе, в котором значение приоритета оказалось меньше .
- Теперь вызываем от найденного элемента (от элемента вместе со всем его поддеревом)
- Полученные и записываем в качестве левого и правого сына добавляемого элемента.
- Полученное дерево ставим на место элемента, найденного в первом пункте.
Remove
Операция удаляет из дерева элемент с ключом .
- Реализация №1
- Разобьём наше дерево по ключу, который мы хотим удалить, то есть .
- Теперь отделяем от первого дерева элемент , опять таки разбивая по ключу , то есть .
- Сливаем первое дерево со вторым, то есть .
- Реализация №2
- Спускаемся по дереву (как в обычном бинарном дереве поиска по ), ища удаляемый элемент.
- Найдя элемент, вызываем его левого и правого сыновей
- Возвращаемое значение функции ставим на место удаляемого элемента.
Высота декартового дерева
Мы уже выяснили, что сложность операций с декартовым деревом линейно зависит от его высоты. В действительности высота декартова дерева может быть линейной относительно его размеров. Например, высота декартова дерева, построенного по набору ключей , будет равна . Во избежание таких случаев, полезным оказывается выбирать приоритеты в ключах случайно.
| Теорема: | ||||||
Декартово дерево из узлов, ключи которых являются незавимыми непрерывными случайными величинами с одинаковым вероятностным распределением, имеет высоту . | ||||||
| Доказательство: | ||||||
|
Замечание: В следующих утверждениях мы будем считать, что , а каждое выбрано случайно и независимо с одинаковым распределением, а также будем называть -м узлом узел с ключом .
| ||||||