Дерево ван Эмде Боаса — различия между версиями
Warrior (обсуждение | вклад) (→empty) |
Warrior (обсуждение | вклад) (→insert) |
||
| Строка 52: | Строка 52: | ||
== insert == | == insert == | ||
| − | Операция | + | Операция вставки элемента <tex>x</tex> состоит из трех частей частей |
| − | * | + | *обновление полей <tex>min</tex> и <tex>max</tex> текущего дерева, если это требуется |
| − | * | + | *вставка во вспомогательное дерево <tex>aux</tex> числа <tex>high(x)</tex>, если соответствующее поддерево <tex>children[high(x)]</tex> до этого было пусто |
| − | + | *вставка числа <tex>low(x)</tex> в поддерево <tex>children[high(x)]</tex>, за исключением ситуации, когда текущее дерево {{---}} это 1-дерево, и дальнейшая вставка не требуется | |
| − | * | ||
<pre> | <pre> | ||
| − | + | insert(T, x) | |
| − | if (T | + | if empty(T) // проверка на пустоту текущего дерева |
| − | T.min = T.max = x; | + | T.min = x; |
| − | + | T.max = x; | |
| − | if | + | if T.min > x |
| − | + | T.min = x; // релаксация минимума | |
| − | + | if T.max < x | |
| − | + | T.max = x; // релаксация максимума | |
| − | + | if T.k != 1 | |
| − | + | if empty(T.children[high(x)]) | |
| − | if | + | insert(aux, high(x)); // вставка high(x) во вспомогательно дерево aux |
| − | + | insert(T.children[high(x)], low(x)); // вставка low(x) в поддерево children[high(x)] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</pre> | </pre> | ||
Версия 21:33, 7 апреля 2012
| Определение: |
| Дерево ван Эмде Боаса — структура данных, представляющая собой дерево поиска, позволяющее хранить целые неотрицательные числа в интервале и осуществлять над ними все соответствующие дереву поиска операции. |
Проще говоря, данная структура позволяет хранить -битные числа и производить над ними операции , , , , , , и некоторые другие операции, которые присущи всем деревьям поиска.
Особенностью этой структуры является то, что все операции выполняются за , что асимптотически лучше, чем в большинстве других деревьев поиска, где — количество элементов в дереве.
Содержание
Структура
Для удобства работы с деревом будем использовать , равные степени двойки.
Как уже было сказано выше, -дерево хранит числа в интервале . Тогда 1-дерево хранит информацию, содержатся ли в нем 0 и 1.
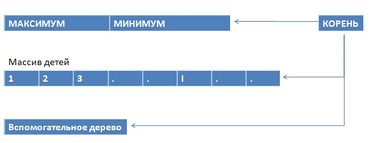
Построим -дерево, при . В нем будут хранится:
- массив , состоящий из -деревьев
- вспомогательное -дерево, которое назовем
- максимальный и минимальный элемент, хранящийся в этом дереве (если оно не является пустым)
Пусть у нас есть -битное число . Разобьем это число таким образом, что — число, соответствующее старшим битам числа , а соответствует младшим битам. Тогда информация, хранится ли в данном дереве число , эквивалентна информации, содержится ли в дереве число .
Нетрудно увидеть, что высота подобного дерева , так как каждый следующий уровень дерева содержит числа, количество битов в которых в 2 раза меньше, чем в предыдущем.
Во вспомогательном дереве будем хранить все такие числа , что дерево не пусто.
Операции
empty
Чтобы определить, пусто ли дерево, будем изначально инициализировать поле числом, которое не лежит в интервале . Назовем это число . Например, это может быть , если мы храним в числа в знаковом целочисленном типе, или , если в беззнаковом. Тогда проверка на пустоту дерева будет заключаться лишь в сравнении поля с этим числом.
empty(T)
if T.min == none
return true;
else
return false;
find
Алгоритм поиска сам напрашивается из выше описанной структуры:
- если дерево пусто, то число не содержится в нашей структуре
- если число равно полю , то число в дереве есть
- иначе ищем число в поддереве
find(T, x)
if empty(T)
return false;
if T.min == x
return true;
return find(T.children[high(x)], low(x));
insert
Операция вставки элемента состоит из трех частей частей
- обновление полей и текущего дерева, если это требуется
- вставка во вспомогательное дерево числа , если соответствующее поддерево до этого было пусто
- вставка числа в поддерево , за исключением ситуации, когда текущее дерево — это 1-дерево, и дальнейшая вставка не требуется
insert(T, x)
if empty(T) // проверка на пустоту текущего дерева
T.min = x;
T.max = x;
if T.min > x
T.min = x; // релаксация минимума
if T.max < x
T.max = x; // релаксация максимума
if T.k != 1
if empty(T.children[high(x)])
insert(aux, high(x)); // вставка high(x) во вспомогательно дерево aux
insert(T.children[high(x)], low(x)); // вставка low(x) в поддерево children[high(x)]
remove
Удаление из дерева T также делится на несколько подзадач:
- Если T.min = T.max = x, значит в дереве один элемент, мы его удалим и как-нибудь пометим, что дерево пусто(на будущее).
- Если x = T.min,то мы должны найти следующий второй минимум удалить его из того места где он находится и поставить в T.min Второй минимум - это либо T.max, либо T.children[T.aux.min].min.
Аналогично для случая x = T.max
- Если же x = T.min и x = T.max, то мы должны удалить x из поддерева i отвечающего x.
Важно, что Delete реализован рекурсивно от дерева в котором идет удаления. Так же нельзя забывать, что если мы удаляем последнее вхождение x, то мы должны удалить i из вспомогательного дерева.
Delete(T, x)
if (T.min == T.max == x)
T.min = M
T.max = -1
return
if (x == T.min)
if (T.aux is empty)
T.min = T.max
return
else
x = T.children[T.aux.min].min
T.min = x
if (x == T.max)
if (T.aux is empty)
T.max = T.min
return
else
x = T.children[T.aux.max].max
T.max = x
if (T.aux is empty)
return
i = floor(x/sqrt(M))
Delete(T.children[i], x%sqrt(M))
if (T.children[i] is empty)
Delete(T.aux, i)
(с)wikipedia.org