Дерево отрезков. Построение

Дерево отрезков (англ. Segment tree) — это структура данных, которая позволяет за асимптотику [math]O(\log n)[/math] реализовать любые операции, определяемые на моноиде. Например, следующего вида: нахождение суммы (задача RSQ), минимума или максимума (задача RMQ) элементов массива в заданном отрезке [math]a[l],a[l+1],\dots,a[r][/math].

При этом дополнительно возможно изменение элементов массива: как изменение значения одного элемента, так и изменение элементов на целом подотрезке массива, например разрешается присвоить всем элементам [math]a[l \dots r][/math] какое-либо значение, либо прибавить ко всем элементам массива какое-либо число. Структура занимает [math]O(n)[/math] памяти, а ее построение требует [math]O(n)[/math] времени.

Структура

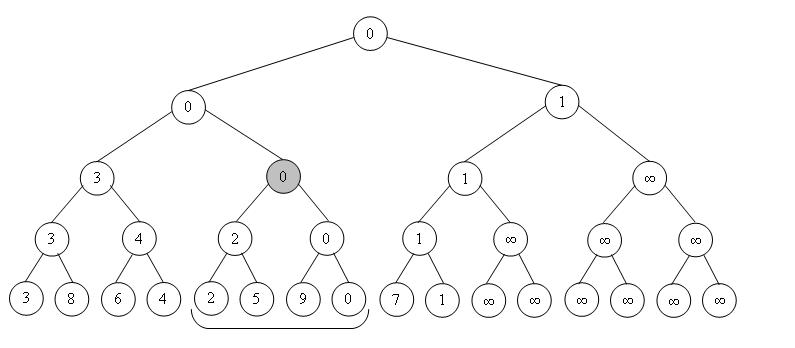
Структура представляет собой дерево, листьями которого являются элементы исходного массива. Другие вершины этого дерева имеют по два ребенка и содержат результат операции от своих детей (например минимум или сумму). Таким образом, корень содержит результат искомой функции от всего массива [math][0 \dots n-1][/math], левый ребёнок корня содержит результат функции на [math][0\dots\frac{n}{2}][/math], а правый, соответственно результат на [math][\frac{n}{2}+1 \dots n-1][/math]. И так далее, продвигаясь вглубь дерева.

Построение дерева

Пусть исходный массив [math]a[/math] состоит из [math]n[/math] элементов. Для удобства построения увеличим длину массива [math]a[/math] так, чтобы она равнялась ближайшей степени двойки, т.е. [math]2^k[/math], где [math]2^k \geqslant n[/math]. Это сделано, для того чтобы не допустить обращение к несуществующим элементам массива при дальнейшем процессе построения. Пустые элементы необходимо заполнить нейтральными элементами моноида. Тогда для хранения дерева отрезков понадобится массив [math]t[/math] из [math]2^{k+1}[/math] элементов, поскольку в худшем случае количество вершин в дереве можно оценить суммой , где [math]n=2^k[/math]. Таким образом, структура занимает линейную память.

Процесс построения дерева заключается в заполнении массива [math]t[/math]. Заполним этот массив таким образом, чтобы [math]i[/math]-й элемент являлся бы результатом некоторой бинарной операции [math]\circ[/math] от элементов c номерами [math]2i+1[/math] и [math]2i+2[/math], то есть родитель являлся результатом бинарной операции от своих сыновей. Один из вариантов — делать рекурсивно. Пусть у нас имеются исходный массив [math]a[/math], а также переменные [math]tl[/math] и [math]tr[/math], обозначающие границы текущего полуинтервала [math][tl, tr)[/math]. Запускаем процедуру построения от корня дерева отрезков ([math]i=0[/math], [math]tl=0[/math], [math]tr=n[/math]), а сама процедура построения, если её вызвали не от листа, вызывает себя от каждого из двух сыновей и суммирует вычисленные значения, а если её вызвали от листа — то просто записывает в себя значение этого элемента массива (Для этого у нас есть исходный массив [math] a [/math]). Асимптотика построения дерева отрезков составит [math]O(n)[/math].

Выделяют два основных способа построения дерева отрезков: построение снизу и построение сверху. При построении снизу алгоритм поднимается от листьев к корню (Просто начинаем заполнять элементы массива [math]t[/math] от большего индекса к меньшему, таким образом при заполнении элемента [math] i [/math] его дети [math]2i+1[/math] и [math]2i+2[/math] уже будут заполнены, и мы с легкостью посчитаем бинарную операцию от них), а при построении сверху спускается от корня к листьям. Особенные изменения появляются в реализации запросов к таким деревьям отрезков.

Реализация построения сверху:

function treeBuild(a[], i, tl, tr):
// Мы находимся в вершине с номером i, который отвечает за полуинтервал [tl, tr)
  if tl == tr 
    return
  if tr - tl == 1
    t[i] = a[tl]
  else
    tm = (tl + tr) / 2 //середина отрезка
    treeBuild(a, 2 * i + 1, tl, tm)
    treeBuild(a, 2 * i + 2, tm, tr)
    t[i] = t[2 * i + 1] [math] \circ [/math] t[2 * i + 2]

Реализация построения снизу:

function treeBuild(a[]):
  for i = n - 1 .. 2 * n - 1
    t[i] = a[i - n - 1]
  for i = n - 2 .. 0
    t[i] = t[2 * i + 1] [math] \circ [/math] t[2 * i + 2]

Персистентное дерево отрезков

Определение:

Персистентной (англ. Persistent) называется такая структура данных, которая хранит все свои промежуточные версии.

Определение:

Полностью персистентной (англ. Fully persistent) называется такая персистентная структура данных, в которой разрешено изменять любую её версию и делать запросы к любой её версии.

На основе дерева отрезков можно построить полностью персистентную структуру данных.

Структура дерева

Для реализации персистентного дерева отрезков удобно несколько изменить структуру дерева. Для этого будем использовать явные указатели [math]L[/math] и [math]R[/math] для дочерних элементов. Кроме того, заведем массив [math]roots[][/math], в котором [math]roots[i][/math] указывает на корень дерева отрезков версии [math]i[/math]

Построение

Для построения персистентного дерева отрезков из [math]n[/math] элементов необходимо пройтись по всему дереву, попутно создавая все необходимые вершины. В листах создавать вершину, хранящую соответствующее значение. Промежуточные же вершины строим от левого и правого сыновей

function treeBuild(a[], tl, tr):
  if tl == tr
    return Vertex(a[tl])
  tm = (tl + tr) / 2
  return Vertex(treeBuild(a[], tl, tm), treeBuild(a[], tm, tr))

Изменение элемента

Для того, чтобы изменить элемент в персистентном дереве отрезков, необходимо сделать следующие действия: спустимся в дереве от корня нужной версии до требуемого элемента, скопируем его, изменим значение, и, поднимаясь по дереву, будем клонировать узлы. При этом необходимо менять указатель на одного из детей на узел, созданный при предыдущем клонировании. После копирования корня, добавим новый корень в конец массива корней.

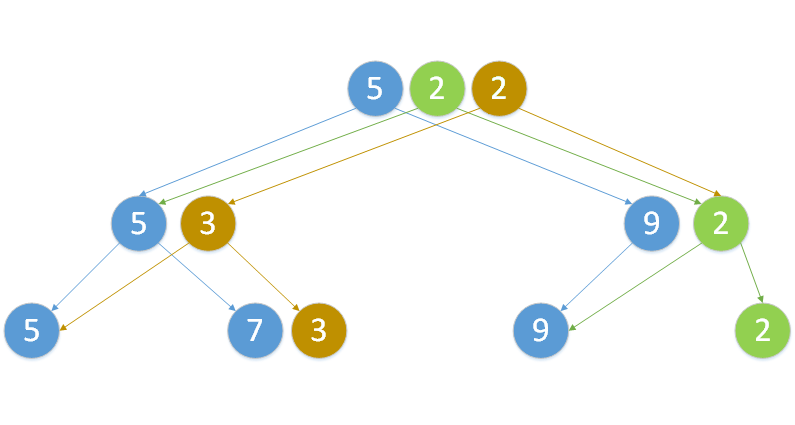
Пример дерева отрезков для операции минимум:

Здесь изображено персистентное дерево отрезков с операцией минимум, в котором изначально было [math]3[/math] элемента. Сперва к нему была добавлена вершина со значением [math]2[/math], а потом изменена вершина со значением [math]7[/math]. Цвет ребер и вершин соответствует времени их появления. Синий цвет элементов означает, что они были изначально, зеленый — что они появились после добавления, а оранжевый — что они появились после изменения элемента.

 function update(v, tl, tr, pos, val):
    if tr - tl == 1
      return Vertex(val)
    tm = (tl + tr) / 2
    if pos [math]\leqslant[/math] tm
      return Vertex(update(v.l, tl, tm, pos, val), v.r)
    else
      return Vertex(v.l, update(v.r, tm, tr, pos, val))