Дерево палиндромов — различия между версиями
(→Построение) |
(→Описание структуры) |
||
| Строка 25: | Строка 25: | ||
<tex>root_{even}</tex> будет соответствовать фиктивному палиндрому длины 0. | <tex>root_{even}</tex> будет соответствовать фиктивному палиндрому длины 0. | ||
| − | Также направим суффиксные ссылки обоих корней к вершине <tex>root_{odd} | + | Также направим суффиксные ссылки обоих корней к вершине <tex>root_{odd}</tex>. |
== Построение == | == Построение == | ||
Версия 20:48, 6 июня 2016
Дерево палиндромов — структура данных, позволяющая решить некоторые интересные задачи на палиндромы.
Эту структуру данных придумал Михаил Рубинчик и рассказал ее на летних сборах в Петрозаводске в 2014 году.
Содержание
Описание структуры
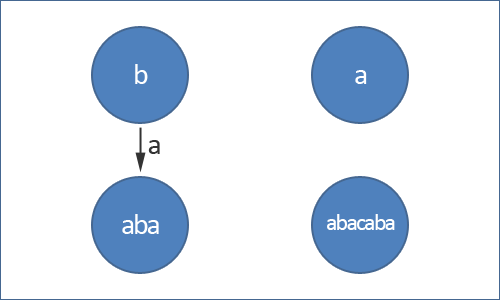
Дерево палиндромов состоит из вершин. Каждая вершина соответствует палиндрому. Через будем обозначать строку, которой соответствует вершина .
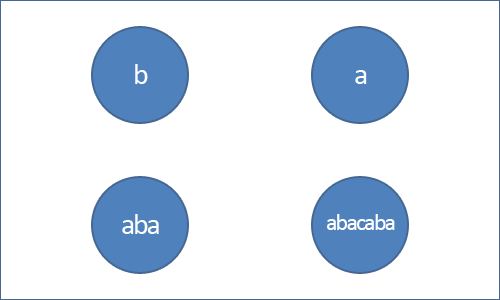
Ребра дерева палиндромов ориентированные и помечены символами. Ребро с символом из вершины в вершину означает, что . Тут означает конкатенацию строк.
Также в дереве палиндромов присутствуют суффиксные ссылки. Суффиксная ссылка из вершины ведет в вершину , если является наибольшим суффиксом строки .
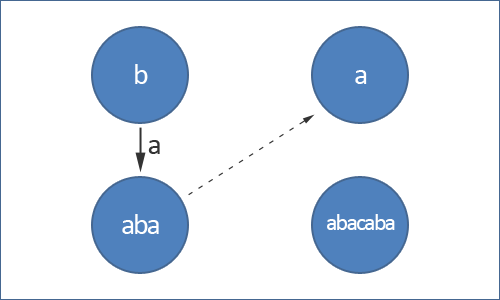
Название структуры данных выбрано не совсем удачно, т.к. на самом деле она представляет из себя два дерева, однако суффиксные ссылки могут вести как в то же, так и в другое дерево. Это сделано для удобства реализации. Также в целях экономии памяти мы не будем хранить для каждой вершины соответствующую ей строку-палиндром. Вместо этого мы будем хранить только длину палиндрома.
Итак, у нас будет два дерева. Одно дерево для палиндромов четной длины, другое — для палиндромов нечетной длины. Каждое дерево будет иметь фиктивный корень. Обозначим корни четного и нечетного дерева соответственно и .
будет соответствовать фиктивному палиндрому длины -1. Это нужно для того, чтобы не обрабатывать отдельно случай добавления палиндрома длины 1. Теперь каждый раз при добавлении новой вершины к вершине мы будем просто указывать ее длину равной .
будет соответствовать фиктивному палиндрому длины 0.
Также направим суффиксные ссылки обоих корней к вершине .
Построение
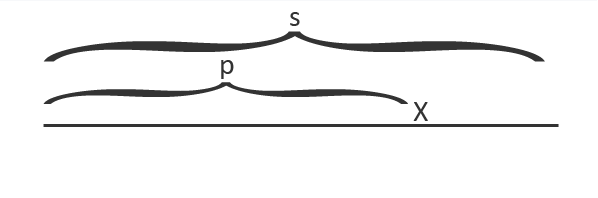
Будем обрабатывать строку символ за символом. Пусть мы уже обработали некоторый префикс и теперь хотим добавить следующий символ строки, назовем его .
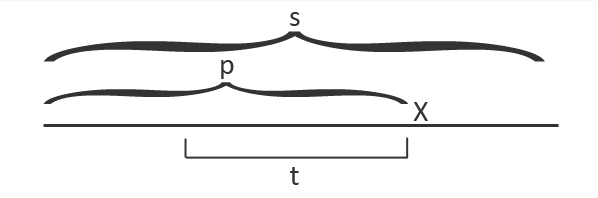
Будем также поддерживать максимальный палиндром-суффикс обработанного префикса . Назовем его .
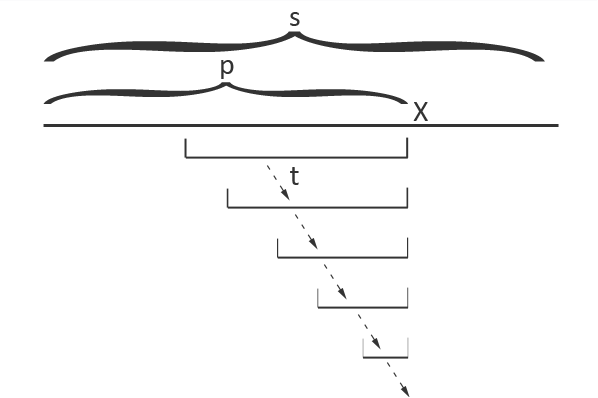
Т.к. находится в уже обработанной части строки, то ему соответствует какая-то вершина в дереве. У этой вершины есть суффиксная ссылка на какую-то другую вершину, у которой тоже есть суффиксная ссылка и т.д.
Найдем теперь палиндром-суффикс нового префикса, состоящего из и . Искомый палиндром-суффикс будет иметь вид , где — это какая-то строка, возможно пустая (или фиктивный строка длины -1, соответствующая корню , если искомый палиндром-суффикс — это просто символ ). Т.к. палиндром, то — тоже палиндром, и, более того, это суффикс строки . Поэтому он может быть достигнут из по суффиксным ссылкам.
Строка — это единственная подстрока-палиндром строки , которой, возможно, нет в (все другие подстроки-палиндромы есть). Чтобы понять почему это так, нужно обратить внимание на то, что все новые подстроки-палиндромы, которых не было в , должны оканчиваться на символ , и поэтому должны быть палиндромом-суффиксом строки . Из-за того, что — наибольший палиндром-суффикс строки , все остальные меньшие палиндромы-суффиксы этой строки уже есть в каком-то префиксе строки (т.к. для каждого суффикса палиндрома есть равный ему префикс) и, соответственно, уже есть в .
Таким образом, чтобы обработать очередной символ , нужно просто спуститься по суффиксным ссылкам строки до тех пор, пока мы не найдем подходящую строку (причем мы всегда можем найти такую строку, возможно длины -1, если очередная суффиксная ссылка будет вести в корень). Затем нужно проверить, есть ли уже ребро по символу из вершины, соответствующей , и если нет, добавить это ребро в новую вершину .
Теперь нужно добавить суффиксную ссылку из вершины . Если эта вершина уже существовала до добавления символа , ничего делать не нужно — суффиксная ссылка итак указывает на правильную вершину. Иначе на нужно найти наибольший палиндром-суффикс строки , который будет иметь вид , где — это некоторая строка, возможно, пустая. Следуя той же логике, которую мы использовали раньше, — это палиндром-суффикс строки и может быть достигнут из по суффиксным ссылкам.