Дерево решений и случайный лес — различия между версиями
Sokolova (обсуждение | вклад) (→Рекурсивный алгоритм построения бинарного дерева решений ID3) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 49 промежуточных версий 7 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Дерево решений {{---}} логический алгоритм классификации, решающий задачи классификации и регрессии. | + | Дерево решений {{---}} логический алгоритм классификации, решающий задачи классификации и регрессии. Представляет собой объединение логических условий в структуру дерева. |
==Дерево решений== | ==Дерево решений== | ||
| Строка 8: | Строка 8: | ||
|definition= | |definition= | ||
'''Дерево решений''' (англ. ''decision tree, DT'') {{---}} алгоритм классификации <tex>a(x) = (V_{внутр}, v_0, V_{лист}, S_v, \beta_v)</tex>, задающийся деревом (связным ациклическим графом), где: | '''Дерево решений''' (англ. ''decision tree, DT'') {{---}} алгоритм классификации <tex>a(x) = (V_{внутр}, v_0, V_{лист}, S_v, \beta_v)</tex>, задающийся деревом (связным ациклическим графом), где: | ||
| − | * <tex> V = V_{внутр} \cup V_{лист} </tex> {{---}} множество вершин , <tex>v_0 \in V</tex> {{---}} корень дерева | + | * <tex> V = V_{внутр} \cup V_{лист} </tex> {{---}} множество вершин , <tex>v_0 \in V</tex> {{---}} корень дерева; |
| − | * <tex> S_v : D_v \rightarrow V_v </tex> {{---}} функция перехода по значению предиката в множество детей вершины <tex>v</tex> | + | * <tex> S_v : D_v \rightarrow V_v </tex> {{---}} функция перехода по значению предиката в множество детей вершины <tex>v</tex>; |
| − | * <tex> \beta_v : X \rightarrow D_v </tex> {{---}} предикат ветвления, <tex>v \in V_{внутр}</tex> и <tex>|D_v| < \infty</tex> | + | * <tex> \beta_v : X \rightarrow D_v </tex> {{---}} предикат ветвления, <tex>v \in V_{внутр}</tex> и <tex>|D_v| < \infty</tex>; |
| − | * Для листьев <tex>v \in V_{лист}</tex> определена метка класса <tex>y_v \in Y</tex> | + | * Для листьев <tex>v \in V_{лист}</tex> определена метка класса <tex>y_v \in Y</tex>. |
}} | }} | ||
{{Определение | {{Определение | ||
| Строка 23: | Строка 23: | ||
'''function''' classify(x): | '''function''' classify(x): | ||
<tex>v = v_0</tex> | <tex>v = v_0</tex> | ||
| − | '''if''' <tex>\beta_v(x) = 1 </tex> | + | '''if''' <tex>\beta_v(x) = 1 </tex> |
<tex>v := R_v</tex> | <tex>v := R_v</tex> | ||
'''else''' | '''else''' | ||
<tex>v := L_v</tex> | <tex>v := L_v</tex> | ||
'''return''' <tex>y_v</tex> | '''return''' <tex>y_v</tex> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Информативность ветвления=== | ===Информативность ветвления=== | ||
| + | Для того, чтобы оценивать качество разбиения объектов по предикату <tex>\beta</tex>, введем понятие ''информационного выигрыша'' разбиения. <br> | ||
| + | Сначала оценим распределение значений классов объектов внутри каждого множества из разбиения, введя понятие ''меры неопределенности распределения''. | ||
{{Определение | {{Определение | ||
|id=def1 | |id=def1 | ||
| Строка 70: | Строка 45: | ||
|definition= | |definition= | ||
'''Мера неопределенности (англ. ''impurity'') распределения <tex>p_y</tex>''': <br> | '''Мера неопределенности (англ. ''impurity'') распределения <tex>p_y</tex>''': <br> | ||
| − | * минимальна, когда <tex>p_y \in \{0,1\}</tex> | + | * минимальна, когда <tex>p_y \in \{0,1\}</tex>; |
| − | * максимальна, когда <tex>p_y = \frac{1}{|Y|}</tex> для всех <tex>y \in Y</tex> | + | * максимальна, когда <tex>p_y = \frac{1}{|Y|}</tex> для всех <tex>y \in Y</tex>; |
* не зависит от перенумерации классов | * не зависит от перенумерации классов | ||
<tex>Ф(U) = \sum\nolimits_{y \in Y} p_y L(p_y) = \frac{1}{|U|} \sum\nolimits_{x_i \in U}L(P(y_i | x_i \in U)) \rightarrow min</tex>, <br> где <tex>L(p)</tex> убывает и <tex>L(1) = 0</tex>, например: <tex>-log_2(p)</tex>, <tex>1 - p</tex>, <tex>1 - p^2</tex> | <tex>Ф(U) = \sum\nolimits_{y \in Y} p_y L(p_y) = \frac{1}{|U|} \sum\nolimits_{x_i \in U}L(P(y_i | x_i \in U)) \rightarrow min</tex>, <br> где <tex>L(p)</tex> убывает и <tex>L(1) = 0</tex>, например: <tex>-log_2(p)</tex>, <tex>1 - p</tex>, <tex>1 - p^2</tex> | ||
}} | }} | ||
| − | + | ||
| − | * Энтропия: <tex>Ф(U) = -\sum\ | + | Примерами мер неопределенности распределения являются: |
| − | * Критерий Джини: <tex>Ф(U) = \sum\nolimits_{i != j}p_i p_j = \sum\nolimits_{i}p_i*(1-p_i)</tex> | + | * Энтропия: <tex>Ф(U) = -\sum\limits_{i}^N p_i log_2p_i</tex>, определяется для каждого множества из разбиения, <tex>N</tex> {{---}} количество возможных классов, и <tex>p_i</tex> {{---}} вероятность объекта принадлежать <tex> i</tex>-ому классу. |
| + | * Критерий Джини: <tex>Ф(U) = \sum\nolimits_{i != j}p_i p_j = \sum\nolimits_{i}p_i*(1-p_i)</tex>, максимизацию этого критерия можно интерпретировать как максимизацию числа пар объектов одного класса, оказавшихся после разбиения в одном множестве. <br> | ||
| + | |||
| + | Теперь определим суммарную ''неопределенность распределения'' в разбиении. | ||
{{Определение | {{Определение | ||
|id=def1 | |id=def1 | ||
| Строка 86: | Строка 64: | ||
}} | }} | ||
| + | ''Информационный выигрыш'' от разбиения определяется как изменение неопределенности в системе. | ||
{{Определение | {{Определение | ||
|id=def1 | |id=def1 | ||
|neat = | |neat = | ||
|definition= | |definition= | ||
| − | '''Информационный выигрыш от | + | '''Информационный выигрыш от разбиения по предикату <tex>\beta</tex>''' <br> |
<tex>Gain(\beta, U) = Ф(U) - Ф(U_1, ... ,U_{|D_v|}) = Ф(U) - \sum\nolimits_{k \in D_v} \frac{|U_k|}{|U|}Ф(U_k) \rightarrow max_{\beta \in B} </tex> | <tex>Gain(\beta, U) = Ф(U) - Ф(U_1, ... ,U_{|D_v|}) = Ф(U) - \sum\nolimits_{k \in D_v} \frac{|U_k|}{|U|}Ф(U_k) \rightarrow max_{\beta \in B} </tex> | ||
}} | }} | ||
| + | |||
| + | === Рекурсивный алгоритм построения бинарного дерева решений ID3 === | ||
| + | Покажем идею построения дерева решения на частном случае бинарного дерева. Алгоритм <tex>ID3</tex> (англ. ''Induction of Decision Tree'') заключается в последовательном дроблении выборки на две части до тех пор, пока в каждой части не окажутся объекты только одного класса. Разделение производится по предикату <tex>\beta</tex>, который выбирается из множества элементарных предикатов. На практике в качестве элементарных предикатов чаще всего берут простые пороговые условия вида <tex>\beta(x) = [f_j(x) >= d_j]</tex>. | ||
| + | <br>Проще всего записать этот алгоритм в виде рекурсивной процедуры <tex>ID3</tex>, которая строит дерево по заданной подвыборке <tex>U</tex> и возвращает его корневую вершину. | ||
| + | |||
| + | 1:'''function''' ID3(<tex>U</tex>): | ||
| + | 2: '''if''' <tex>for all</tex> <tex>u \in U</tex>: <tex>y_u = y</tex>, <tex>y \in Y</tex> | ||
| + | <font color=green>// создать листовую вершину <tex>v</tex> c меткой класса <tex>y_v</tex> </font> | ||
| + | 3: v = createLeafVertex(<tex>y_v</tex>) | ||
| + | 4: '''return''' v | ||
| + | <font color=green>// найти предикат с максимальным информационным выигрышом </font> | ||
| + | <tex>\beta= \mathrm{arg}\max_{\beta\in B} </tex> Gain(<tex>\beta</tex>, <tex>U</tex>) | ||
| + | <font color=green>// разбить выборку на две части <tex>U = U_0 \cup U_1</tex> по предикату <tex>\beta</tex> </font> | ||
| + | 5: <tex>U_0 := \{x \in U: \beta(x) = 0\}</tex> | ||
| + | 6: <tex>U_1 := \{x \in U: \beta(x) = 1\}</tex> | ||
| + | 7: '''if''' <tex>U_0 = \emptyset</tex> || <tex>U_1 = \emptyset</tex> | ||
| + | <font color=green>// найти класс, в котором находится большинство объектов из <tex>U</tex> </font> | ||
| + | 8: <tex>y_v</tex> = majorClass(<tex>U</tex>) | ||
| + | 9: v = createLeafVertex(<tex>y_v</tex>) | ||
| + | '''else''' | ||
| + | <font color=green>// создать внутреннюю вершину <tex>v</tex></font> | ||
| + | 10: v = createVertex() | ||
| + | 11: <tex>\beta_v = \beta</tex> | ||
| + | 12: <tex>S_0</tex> = ID3(<tex>U_0</tex>) | ||
| + | 13: <tex>S_1</tex> = ID3(<tex>U_1</tex>) | ||
| + | 14: '''return''' <tex>v</tex> | ||
== Редукция решающих деревьев == | == Редукция решающих деревьев == | ||
| − | Суть редукции состоит в удалении поддеревьев, имеющих недостаточную статистическую надёжность. При этом дерево перестаёт безошибочно классифицировать обучающую выборку, зато качество классификации новых объектов, как правило, улучшается. Рассмотрим наиболее простые варианты редукции. | + | Суть редукции (англ. ''pruning'') состоит в удалении поддеревьев, имеющих недостаточную статистическую надёжность. При этом дерево перестаёт безошибочно классифицировать обучающую выборку, зато качество классификации новых объектов, как правило, улучшается. Рассмотрим наиболее простые варианты редукции. |
===Предредукция=== | ===Предредукция=== | ||
| Строка 114: | Строка 119: | ||
* <tex>r_R(v)</tex> — классификация поддеревом правой дочерней вершины <tex>R_v</tex>; | * <tex>r_R(v)</tex> — классификация поддеревом правой дочерней вершины <tex>R_v</tex>; | ||
* <tex>r_c(v)</tex> — отнесение всех объектов выборки <tex>S_v</tex> к классу <tex>y \in Y</tex>. <br> | * <tex>r_c(v)</tex> — отнесение всех объектов выборки <tex>S_v</tex> к классу <tex>y \in Y</tex>. <br> | ||
| − | Эти величины сравниваются, и | + | Эти величины сравниваются, и в зависимости от того, какая из них оказалась |
минимальной, принимается, соответственно, одно из четырёх решений: <br> | минимальной, принимается, соответственно, одно из четырёх решений: <br> | ||
* сохранить поддерево вершины <tex>v</tex>; | * сохранить поддерево вершины <tex>v</tex>; | ||
| Строка 122: | Строка 127: | ||
== Алгоритмы построения деревьев решения == | == Алгоритмы построения деревьев решения == | ||
| − | + | Недостатки рассмотренного алгоритма ID3: | |
| − | * | + | * Применим только для дискретных значений признаков; |
| − | * | + | * Переобучение; |
| − | * | + | * На каждом шаге решение принимается по одному атрибуту. |
| − | == | + | === Алгоритм [https://en.wikipedia.org/wiki/Predictive_analytics#Classification_and_regression_trees_.28CART.29 CART] (англ. ''Classification And Regression Trees'')=== |
| − | + | * В отличие от ID3 работает и с непрерывными значениями признаков: на каждом шаге построения дерева последовательно сравнивает все возможные разбиения для всех атрибутов и выбирает наилучший атрибут и наилучшее разбиение для него. Разбивает объекты на две части; | |
| − | + | * Использует редукцию для избежания переобучения; | |
| − | + | * Обрабатывает пропущенные или аномальные значения признаков. | |
| − | |||
| − | === | + | === Алгоритм [https://en.wikipedia.org/wiki/C4.5_algorithm C4.5] === |
| − | + | * Также работает и с непрерывными значениями признаков: на каждом шаге построения дерева выбирает правило разбиения по одному из признаков. Разбивает объекты на несколько частей по этому правилу, рекурсивно запускается из полученных подмножеств; | |
| + | * Использует редукцию для избежания переобучения; | ||
| + | * Обрабатывает пропущенные или аномальные значения признаков. | ||
| − | + | == Случайный лес == | |
| − | Алгоритм построения случайного леса, состоящего из <tex>N</tex> деревьев на основе обучающей выборки <tex>X</tex>: | + | Случайный лес {{---}} один из примеров объединения классификаторов в [[Виды_ансамблей|ансамбль]]. <br> |
| + | Алгоритм построения случайного леса, состоящего из <tex>N</tex> деревьев на основе обучающей выборки <tex>X</tex> такой: | ||
'''for''' (n: 1,...,N): | '''for''' (n: 1,...,N): | ||
| − | сгенерировать выборку <tex>X_n</tex> c помощью бутстрэпа | + | <font color=green>// сгенерировать выборку <tex>X_n</tex> c помощью [[Виды_ансамблей#Бутстрэп|бутстрэпа]]</font> |
| − | построить решающее дерево <tex>t_n</tex> по выборке <tex>X_n</tex><br> | + | <tex>X_n</tex> = bootstrap(<tex>X</tex>) |
| + | <font color=green>// построить решающее дерево <tex>t_n</tex> по выборке <tex>X_n</tex></font> | ||
| + | <tex>t_n</tex> = ID3(<tex>X_n</tex>) <br> | ||
| − | Итоговый классификатор | + | Итоговый классификатор {{---}} <tex>a(x) = \frac{1}{N} \sum\limits_{i = 1}^{N} t_i(x)</tex>. Для задачи классификации мы выбираем решение по большинству результатов, выданных классификаторами, а в задаче регрессии {{---}} по их среднему значению. <br> |
| − | Таким образом, случайный лес | + | Таким образом, случайный лес {{---}} бэггинг над решающими деревьями, при обучении которых для каждого разбиения признаки выбираются из некоторого случайного подмножества признаков. |
| − | == Примеры | + | ==Примеры кода== |
| − | *Для решения задач классификации и регрессии используют [https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html#sklearn.tree.DecisionTreeClassifier DecisionTreeClassifier], [https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeRegressor.html#sklearn.tree.DecisionTreeRegressor DecisionTreeRegressor] | + | ===Примеры на языке Python=== |
| + | *Для решения задач классификации и регрессии используют [https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html#sklearn.tree.DecisionTreeClassifier DecisionTreeClassifier], [https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeRegressor.html#sklearn.tree.DecisionTreeRegressor DecisionTreeRegressor]; | ||
*В '''sklearn.ensemble''' также представлены методы классификации, основанные на ансамблях, в том числе: [https://scikit-learn.org/stable/modules/ensemble.html#bagging бэггинг] и [https://scikit-learn.org/stable/modules/ensemble.html#forest случайный лес], которые были описаны выше. | *В '''sklearn.ensemble''' также представлены методы классификации, основанные на ансамблях, в том числе: [https://scikit-learn.org/stable/modules/ensemble.html#bagging бэггинг] и [https://scikit-learn.org/stable/modules/ensemble.html#forest случайный лес], которые были описаны выше. | ||
| − | <br>Так, в этом примере создается бэггинг ансамбль из классификаторов '''KNeighborsClassifier''', каждый из которых обучен на | + | <br>Так, в этом примере создается бэггинг ансамбль из классификаторов '''KNeighborsClassifier''', каждый из которых обучен на случайных подмножествах из 50% объектов из обучающей выборки, и 50% случайно выбранных признаков. |
'''from''' sklearn.ensemble '''import''' BaggingClassifier | '''from''' sklearn.ensemble '''import''' BaggingClassifier | ||
| Строка 157: | Строка 167: | ||
Пример использования классификатора на случайном лесе: | Пример использования классификатора на случайном лесе: | ||
| + | Полную версию кода можно найти [https://scikit-learn.org/stable/auto_examples/classification/plot_classifier_comparison.html#sphx-glr-download-auto-examples-classification-plot-classifier-comparison-py| здесь] | ||
'''from''' sklearn '''import''' RandomForestClassifier | '''from''' sklearn '''import''' RandomForestClassifier | ||
'''from''' sklearn.datasets '''import''' make_classification | '''from''' sklearn.datasets '''import''' make_classification | ||
| − | <font color=green>// сгенерируем | + | <font color=green>// сгенерируем случайную обучающую выборку с классификацией по n_classes классам</font> |
| − | X, y = make_classification( | + | X, y = make_classification(n_features=2, n_redundant=0, n_informative=2, |
| + | random_state=1, n_clusters_per_class=1, n_classes=2) | ||
| + | <font color=green>// разбиваем выборку на обучающую и тестовую </font> | ||
| + | X = StandardScaler().fit_transform(X) | ||
| + | X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.4, random_state=42) | ||
<font color=green>// создадим классификатор на случайном лесе, состоящим из n_estimators деревьев</font> | <font color=green>// создадим классификатор на случайном лесе, состоящим из n_estimators деревьев</font> | ||
| − | + | RandomForestClassifier(max_depth=5, n_estimators=10, max_features=1) | |
| − | + | clf.fit(X_train, y_train) | |
| − | clf.fit( | + | score = clf.score(X_test, y_test) |
| − | clf. | ||
| − | == Пример | + | Результат классификации показан на рисунке. |
| + | |||
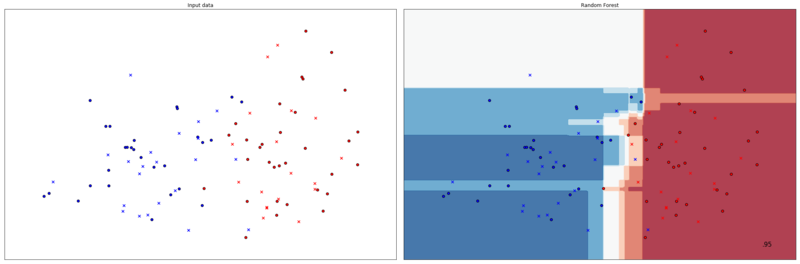
| + | [[Файл:RFC.png |800px|thumb|center|Классификация RandomForestClassifier. Кружочками изображены объекты обучающей выборки, крестиками тестовой выборки. Справа цветом выделены границы принятия решений, в правом нижнем углу {{---}} значение accuracy.]] | ||
| + | |||
| + | ===Пример на языке Scala=== | ||
SBT зависимость: | SBT зависимость: | ||
libraryDependencies '''+=''' "com.github.haifengl" '''%%''' "smile-scala" '''%''' "1.5.2" | libraryDependencies '''+=''' "com.github.haifengl" '''%%''' "smile-scala" '''%''' "1.5.2" | ||
| Строка 185: | Строка 203: | ||
plot(x, y, dt) | plot(x, y, dt) | ||
| − | == | + | ===Пример на языке Java=== |
| − | *[http://www.machinelearning.ru/wiki/images/3/3e/Voron-ML-Logic.pdf | + | Пример классификации с применением <code>weka.classifiers.trees.RandomForest</code><ref>[http://weka.sourceforge.net/doc.dev/weka/classifiers/trees/RandomForest.html Weka, Random Forest]</ref> |
| − | + | ||
| − | + | <code>Maven</code> зависимость: | |
| − | + | <dependency> | |
| + | <groupId>nz.ac.waikato.cms.weka</groupId> | ||
| + | <artifactId>weka-stable</artifactId> | ||
| + | <version>3.8.0</version> | ||
| + | </dependency> | ||
| + | |||
| + | '''import''' weka.classifiers.evaluation.Evaluation; | ||
| + | '''import''' weka.classifiers.trees.RandomForest; | ||
| + | |||
| + | <font color="green">// read dataset</font> | ||
| + | '''var''' trainingDataSet = getDataSet(...); | ||
| + | '''var''' testingDataSet = getDataSet(...); | ||
| + | <font color="green">// create random forest classifier</font> | ||
| + | '''var''' forest = new RandomForest(); | ||
| + | forest.setMaxDepth(15); | ||
| + | forest.setNumFeatures(2); | ||
| + | forest.buildClassifier(trainingDataSet); | ||
| + | <font color="green">// evaluate the model on test dataset and print summary</font> | ||
| + | '''var''' eval = new Evaluation(trainingDataSet); | ||
| + | eval.evaluateModel(forest, testingDataSet); | ||
| + | System.out.println(eval.toSummaryString()); | ||
| + | |||
| + | === Пример на языке R === | ||
| + | {{Main|Примеры кода на R}} | ||
| + | ==== Деревья решений ==== | ||
| + | Для создания деревьев решений используется функция <code>ctree()</code> из пакета <code>party</code>. | ||
| + | |||
| + | <font color="gray"># importing package </font> | ||
| + | install.packages(<font color="green">"party"</font>) | ||
| + | |||
| + | <font color="gray"># reading data</font> | ||
| + | rdata <- read.csv(<font color="green">"input.csv"</font>, <font color="#660099">sep</font> = <font color="green">','</font>, <font color="#660099">header</font> = FALSE) | ||
| + | |||
| + | <font color="gray"># evaluating model</font> | ||
| + | output.tree <- ctree(target ~ x + y + z, <font color="#660099">data</font> = rdata) | ||
| + | |||
| + | <font color="gray"># plotting results</font> | ||
| + | plot(output.tree) | ||
| + | |||
| + | ==== Случайный лес ==== | ||
| + | Для создания случайного леса необходимо импортировать пакет <code>randomForest</code> | ||
| + | |||
| + | <font color="gray"># importing packages </font> | ||
| + | install.packages(<font color="green">"party"</font>) | ||
| + | install.packages(<font color="green">"randomForest"</font>) | ||
| + | |||
| + | <font color="gray"># reading data</font> | ||
| + | rdata <- read.csv(<font color="green">"input.csv"</font>, <font color="#660099">sep</font> = <font color="green">','</font>, <font color="#660099">header</font> = FALSE) | ||
| + | |||
| + | <font color="gray"># creating the forest</font> | ||
| + | output.forest <- randomForest(target ~ x + y + z, <font color="#660099">data</font> = rdata) | ||
| + | |||
| + | <font color="gray"># getting results</font> | ||
| + | print(output.forest) | ||
| + | |||
| + | == См. также == | ||
| + | * [[Виды ансамблей]] | ||
| + | |||
| + | == Источники информации == | ||
| + | # [http://www.machinelearning.ru/wiki/images/3/3e/Voron-ML-Logic.pdf Логические алгоритмы классификации] {{---}} Лекция К. В. Воронцова | ||
| + | # [https://medium.com/open-machine-learning-course/open-machine-learning-course-topic-5-ensembles-of-algorithms-and-random-forest-8e05246cbba7 Случайный лес] {{---}} статья на Medium, Yury Kashnitskiy | ||
| + | # [https://scikit-learn.org/stable/modules/tree.html Деревья решений] {{---}} scikit-learn.org | ||
| + | #[https://scikit-learn.org/stable/modules/ensemble.html Ансамбли классификаторов] — scikit-learn.org. | ||
| + | |||
| + | |||
| + | [[Категория: Машинное обучение]] | ||
| + | [[Категория: Классификация и регрессия]] | ||
Текущая версия на 19:22, 4 сентября 2022
Дерево решений — логический алгоритм классификации, решающий задачи классификации и регрессии. Представляет собой объединение логических условий в структуру дерева.
Содержание
Дерево решений
| Определение: |
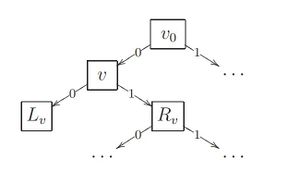
Дерево решений (англ. decision tree, DT) — алгоритм классификации , задающийся деревом (связным ациклическим графом), где:
|
| Определение: |
| Бинарное дерево решений — частный случай дерева решений, для которого . |
function classify(x): if else return
Информативность ветвления
Для того, чтобы оценивать качество разбиения объектов по предикату , введем понятие информационного выигрыша разбиения.
Сначала оценим распределение значений классов объектов внутри каждого множества из разбиения, введя понятие меры неопределенности распределения.
| Определение: |
| Частотная оценка вероятности класса в вершине : |
| Определение: |
Мера неопределенности (англ. impurity) распределения :
где убывает и , например: , , |
Примерами мер неопределенности распределения являются:
- Энтропия: , определяется для каждого множества из разбиения, — количество возможных классов, и — вероятность объекта принадлежать -ому классу.
- Критерий Джини: , максимизацию этого критерия можно интерпретировать как максимизацию числа пар объектов одного класса, оказавшихся после разбиения в одном множестве.
Теперь определим суммарную неопределенность распределения в разбиении.
| Определение: |
| Неопределенность распределения после ветвления вершины по предикату и разбиения : |
Информационный выигрыш от разбиения определяется как изменение неопределенности в системе.
| Определение: |
| Информационный выигрыш от разбиения по предикату |
Рекурсивный алгоритм построения бинарного дерева решений ID3
Покажем идею построения дерева решения на частном случае бинарного дерева. Алгоритм (англ. Induction of Decision Tree) заключается в последовательном дроблении выборки на две части до тех пор, пока в каждой части не окажутся объекты только одного класса. Разделение производится по предикату , который выбирается из множества элементарных предикатов. На практике в качестве элементарных предикатов чаще всего берут простые пороговые условия вида .
Проще всего записать этот алгоритм в виде рекурсивной процедуры , которая строит дерево по заданной подвыборке и возвращает его корневую вершину.
1:function ID3(): 2: if : , // создать листовую вершину c меткой класса 3: v = createLeafVertex() 4: return v // найти предикат с максимальным информационным выигрышом Gain(, ) // разбить выборку на две части по предикату 5: 6: 7: if || // найти класс, в котором находится большинство объектов из 8: = majorClass() 9: v = createLeafVertex() else // создать внутреннюю вершину 10: v = createVertex() 11: 12: = ID3() 13: = ID3() 14: return
Редукция решающих деревьев
Суть редукции (англ. pruning) состоит в удалении поддеревьев, имеющих недостаточную статистическую надёжность. При этом дерево перестаёт безошибочно классифицировать обучающую выборку, зато качество классификации новых объектов, как правило, улучшается. Рассмотрим наиболее простые варианты редукции.
Предредукция
Предредукция (англ. pre-pruning) или критерий раннего останова досрочно прекращает дальнейшее ветвление в вершине дерева, если информативность для всех возможных предикатов не дотягивает до заданного порогового значения .
Для этого на шаге 8 алгоритма условие или заменяется условием . Порог является управляющим параметром метода.
Предредукция считается не самым эффективным способом избежать переобучения, так как жадное ветвление по-прежнему остаётся глобально неоптимальным. Более эффективной считается cтратегия постредукции.
Постредукция
Постредукция (англ. post-pruning) просматривает все внутренние вершины дерева и заменяет отдельные вершины либо одной из дочерних вершин (при этом вторая дочерняя удаляется), либо терминальной вершиной. Процесс замен продолжается до тех
пор, пока в дереве остаются вершины, удовлетворяющие критерию замены.
Критерием замены является сокращение числа ошибок на контрольной выборке, отобранной заранее, и не участвовавшей в обучении дерева. Стандартная рекомендация — оставлять в контроле около 30% объектов.
Для реализации постредукции контрольная выборка пропускается через
построенное дерево. При этом в каждой внутренней вершине запоминается подмножество попавших в неё контрольных объектов. Если , то вершина считается ненадёжной и заменяется терминальной по мажоритарному правилу:
в качестве берётся тот класс, объектов которого больше всего в обучающей подвыборке , пришедшей в вершину .
Затем для каждой внутренней вершины вычисляется число ошибок, полученных при классификации выборки следующими способами:
- — классификация поддеревом, растущим из вершины ;
- — классификация поддеревом левой дочерней вершины ;
- — классификация поддеревом правой дочерней вершины ;
- — отнесение всех объектов выборки к классу .
Эти величины сравниваются, и в зависимости от того, какая из них оказалась
минимальной, принимается, соответственно, одно из четырёх решений:
- сохранить поддерево вершины ;
- заменить поддерево вершины поддеревом левой дочерней вершины ;
- заменить поддерево вершины поддеревом правой дочерней вершины ;
- заменить поддерево терминальной вершиной класса .
Алгоритмы построения деревьев решения
Недостатки рассмотренного алгоритма ID3:
- Применим только для дискретных значений признаков;
- Переобучение;
- На каждом шаге решение принимается по одному атрибуту.
Алгоритм CART (англ. Classification And Regression Trees)
- В отличие от ID3 работает и с непрерывными значениями признаков: на каждом шаге построения дерева последовательно сравнивает все возможные разбиения для всех атрибутов и выбирает наилучший атрибут и наилучшее разбиение для него. Разбивает объекты на две части;
- Использует редукцию для избежания переобучения;
- Обрабатывает пропущенные или аномальные значения признаков.
Алгоритм C4.5
- Также работает и с непрерывными значениями признаков: на каждом шаге построения дерева выбирает правило разбиения по одному из признаков. Разбивает объекты на несколько частей по этому правилу, рекурсивно запускается из полученных подмножеств;
- Использует редукцию для избежания переобучения;
- Обрабатывает пропущенные или аномальные значения признаков.
Случайный лес
Случайный лес — один из примеров объединения классификаторов в ансамбль.
Алгоритм построения случайного леса, состоящего из деревьев на основе обучающей выборки такой:
for (n: 1,...,N): // сгенерировать выборку c помощью бутстрэпа = bootstrap() // построить решающее дерево по выборке = ID3()
Итоговый классификатор — . Для задачи классификации мы выбираем решение по большинству результатов, выданных классификаторами, а в задаче регрессии — по их среднему значению.
Таким образом, случайный лес — бэггинг над решающими деревьями, при обучении которых для каждого разбиения признаки выбираются из некоторого случайного подмножества признаков.
Примеры кода
Примеры на языке Python
- Для решения задач классификации и регрессии используют DecisionTreeClassifier, DecisionTreeRegressor;
- В sklearn.ensemble также представлены методы классификации, основанные на ансамблях, в том числе: бэггинг и случайный лес, которые были описаны выше.
Так, в этом примере создается бэггинг ансамбль из классификаторов KNeighborsClassifier, каждый из которых обучен на случайных подмножествах из 50% объектов из обучающей выборки, и 50% случайно выбранных признаков.
from sklearn.ensemble import BaggingClassifier from sklearn.neighbors import KNeighborsClassifier bagging = BaggingClassifier(KNeighborsClassifier(), max_samples=0.5, max_features=0.5)
Пример использования классификатора на случайном лесе: Полную версию кода можно найти здесь
from sklearn import RandomForestClassifier
from sklearn.datasets import make_classification
// сгенерируем случайную обучающую выборку с классификацией по n_classes классам
X, y = make_classification(n_features=2, n_redundant=0, n_informative=2,
random_state=1, n_clusters_per_class=1, n_classes=2)
// разбиваем выборку на обучающую и тестовую
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.4, random_state=42)
// создадим классификатор на случайном лесе, состоящим из n_estimators деревьев
RandomForestClassifier(max_depth=5, n_estimators=10, max_features=1)
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
Результат классификации показан на рисунке.
Пример на языке Scala
SBT зависимость:
libraryDependencies += "com.github.haifengl" %% "smile-scala" % "1.5.2"
Пример классификации датасета и вычисления F1 меры[1] используя smile.classification.cart[2]:
import smile.classification._ import smile.data._ import smile.plot._ import smile.read import smile.validation.FMeasure
val iris: AttributeDataset = read.table("iris.csv", delimiter = ",", response = Some((new NumericAttribute("class"), 2)))
val x: Array[Array[Double]] = iris.x()
val y: Array[Int] = iris.y().map(_.toInt)
val dt: DecisionTree = cart(x, y, 1000)
val predictions: Array[Int] = x.map(dt.predict)
val f1Score = new FMeasure().measure(predictions, y)
plot(x, y, dt)
Пример на языке Java
Пример классификации с применением weka.classifiers.trees.RandomForest[3]
Maven зависимость:
<dependency> <groupId>nz.ac.waikato.cms.weka</groupId> <artifactId>weka-stable</artifactId> <version>3.8.0</version> </dependency>
import weka.classifiers.evaluation.Evaluation; import weka.classifiers.trees.RandomForest;
// read dataset var trainingDataSet = getDataSet(...); var testingDataSet = getDataSet(...); // create random forest classifier var forest = new RandomForest(); forest.setMaxDepth(15); forest.setNumFeatures(2); forest.buildClassifier(trainingDataSet); // evaluate the model on test dataset and print summary var eval = new Evaluation(trainingDataSet); eval.evaluateModel(forest, testingDataSet); System.out.println(eval.toSummaryString());
Пример на языке R
Деревья решений
Для создания деревьев решений используется функция ctree() из пакета party.
# importing package
install.packages("party")
# reading data
rdata <- read.csv("input.csv", sep = ',', header = FALSE)
# evaluating model
output.tree <- ctree(target ~ x + y + z, data = rdata)
# plotting results
plot(output.tree)
Случайный лес
Для создания случайного леса необходимо импортировать пакет randomForest
# importing packages
install.packages("party")
install.packages("randomForest")
# reading data
rdata <- read.csv("input.csv", sep = ',', header = FALSE)
# creating the forest
output.forest <- randomForest(target ~ x + y + z, data = rdata)
# getting results
print(output.forest)
См. также
Источники информации
- Логические алгоритмы классификации — Лекция К. В. Воронцова
- Случайный лес — статья на Medium, Yury Kashnitskiy
- Деревья решений — scikit-learn.org
- Ансамбли классификаторов — scikit-learn.org.