Задача о числе путей в ациклическом графе

Задача о числе путей в ациклическом графе - одна из классических задач на тему динамического программирования. В этой задаче нам дан ациклический граф [math]G[/math] и две вершины [math]s[/math] и [math]t[/math]. Необходимо посчитать количество путей из вершины [math]s[/math] в вершину [math]t[/math] по рёбрам графа [math]G[/math].

Число таких путей может быть велико даже на небольших графах, поэтому перебор всех возможных вариантов займет много времени. Однако, данную задачу можно решить гораздо быстрее с помощью динамики.

Решение задачи

Перебор всех возможных путей

Небольшая модификация алгоритма обхода в глубину. Запустим обход в глубину от вершины [math]s[/math]. При каждом посещении вершины [math]v[/math] проверим, не является ли она искомой вершиной [math]t[/math]. Если это так, то ответ увеличивается на единицу и обход прекращается. В противном случае производится запуск обхода в глубину от всех вершин, ребра в которые выходят из [math]v[/math], причем он производится независимо от того, были ли эти вершины посещены ранее, или нет.

Функция [math]countPaths(s, t)[/math] принимает начальную вершину [math]s[/math] и конечную вершину [math]t[/math]. В глобальной переменной [math]answer[/math] содержится ответ.

answer = 0

count(v)
    if v == t
        answer += 1
    else
        for(всех [math]to[/math] смежных с [math]v[/math])
            count(to)

countPaths(s, t)
    answer = 0
    count(s)
    return answer

Время работы данного алгоритма в худшем случае [math]O(Ans)[/math], где [math]Ans[/math] - количество путей в графе.

Метод динамического программирования

Пусть [math]P(v)[/math] - количество путей до вершины [math]v[/math]. Можно заметить, что [math]P(v)[/math] зависит только от вершин, ребра из которых входят в [math]v[/math]. Тогда [math]P(v) = \sum\limits_{c}P(c)[/math] таких [math]c[/math], что [math]\exists[/math] ребро из [math]c[/math] в [math]v[/math]. Мы свели нашу задачу к более мелким подзадачам, причем мы также знаем, что [math]P(s) = 1[/math]. Это позволяет решить задачу методом динамического программирования.

Псевдокод

Пусть [math]s[/math] - стартовая вершина, а [math]t[/math] - конечная, для нее и посчитаем ответ. Будем поддерживать массив [math]d[/math], где [math]d[v][/math] - количество путей до вершины [math]v[/math] и массив [math]w[/math], где [math]w[v] = true[/math], если ответ для вершины [math]v[/math] уже посчитан, и [math]w[v] = false[/math] в противном случае. Изначально [math]w[i] = false[/math] для всех вершин [math]i[/math], кроме [math]s[/math], а [math]d[s] = 1[/math]. Функция [math]count(v)[/math] будет возвращать ответ для вершины [math]v[/math]. Удобнее всего это реализовать с помощью ленивой рекурсии, тогда значения массива [math]d[/math] будут вычисляться по мере необходимости, а засчет запоминания результатов они не будут считаться лишний раз:

[math] count(v) = \left \{ \begin{array}{ll} d[v], & w[v]=true \\ \sum\limits_{c}count(c), & w[v]=false \end{array} \right. [/math]

count(v)
    if w[v]
        return d[v]
    else
        sum = 0
        for(всех [math]c[/math] смежных с [math]v[/math])
            sum += count(c)
        d[v] = sum
        w[v] = true
        return sum

countPaths(s, t)
    d[s] = 1
    w[s] = true
    answer = count(t)
    return answer

Значение функции [math]count(v)[/math] считается для каждой вершины один раз, а внутри нее рассматриваются все такие ребра [math]\{e\ |\ end(e) = v\}[/math]. Всего таких ребер для всех вершин в графе [math]O(E)[/math], следовательно, время работы алгоритма в худшем случае оценивается как [math]O(V+E)[/math], где [math]V[/math] - количество вершин графа, [math]E[/math] - количество ребер.

Пример работы

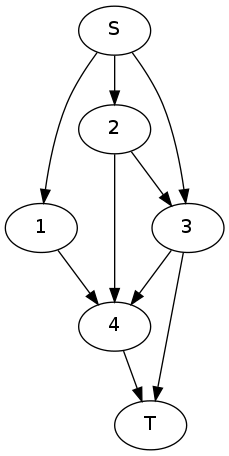
Рассмотрим пример работы алгоритма на следующем графе:

description

Изначально массивы [math]d[/math] и [math]w[/math] инициализированы следующим образом:

вершина	S	1	2	3	4	T
w	true	false	false	false	false	false
d	1	0	0	0	0	0

Сначала функция [math]count[/math] будет вызвана от вершины [math]T[/math]. Ответ для нее еще не посчитан ([math]w[T] = false[/math]), следовательно [math]count[/math] будет вызвана от вершин [math]3[/math] и [math]4[/math]. Для вершины [math]3[/math] ответ также не посчитан ([math]w[3] = false[/math]), следовательно [math]count[/math] будет вызвана уже для вершин [math]2[/math] и [math]S[/math]. А вот для них ответ мы уже можем узнать: для [math]2[/math] он равен [math]d[S][/math], так как это [math]S[/math] - единствнная вершина, ребро из которой входит в нее. Непосредственно для [math]S[/math] ответ нам также известен. На текущий момент таблица будет выглядеть следующим образом:

вершина	S	1	2	3	4	T
w	true	false	true	false	false	false
d	1	0	1	0	0	0

Теперь мы знаем значения для вершин [math]2[/math] и [math]S[/math], что позволяет вычислить [math]d[3] = d[2] + d[S] = 2[/math]. Также обновим значения в массиве [math]w[/math]: [math]w[3] = true[/math].

вершина	S	1	2	3	4	T
w	true	false	true	true	false	false
d	1	0	1	2	0	0

В самом начале для вычисления [math]d[T][/math] нам требовались значения [math]d[3][/math] и [math]d[4][/math]. Теперь нам известно значение [math]d[3][/math], поэтому проследим за тем, как будет вычисляться [math]d[4][/math]. [math]d[4] = count(3) + count(2) + count(1)[/math], но [math]w[3] = true, w[2] = true[/math], следовательно значения [math]d[3][/math] и [math]d[2][/math] мы уже знаем, и нам необходимо вызвать [math]count(1)[/math]. Ответ для этой вершины равен [math]d[S][/math], так как это единственная вершина, ребро из которой входит в [math]1[/math]. Обновим соответствующие значения массивов [math]d[/math] и [math]w[/math]:

вершина	S	1	2	3	4	T
w	true	true	true	true	false	false
d	1	1	1	2	0	0

Теперь нам известны все три значения, требующиеся для вычисления ответа для вершины [math]4[/math]. [math]d[4] = d[3] + d[2] + d[1] = 2 + 1 + 1 = 4[/math]:

вершина	S	1	2	3	4	T
w	true	true	true	true	true	false
d	1	1	1	2	4	0

Наконец, вычислим [math]d[T] = d[3] + d[4] = 2 + 4 = 6[/math] и обновим таблицы [math]d[/math] и[math]w[/math]:

вершина	S	1	2	3	4	T
w	true	true	true	true	true	true
d	1	1	1	2	4	6

Этот алгоритм позволяет вычислить количество путей от какой-либо вершины [math]S[/math] не только до [math]T[/math], но и для любой вершины, лежащей на любом из путей от [math]S[/math] до [math]T[/math]. Для этого достаточно взять значение в соответствующей ячейке [math]d[/math].