Интерактивные протоколы. Класс IP. Класс AM — различия между версиями
Kirelagin (обсуждение | вклад) (→Класс IP) |
м (rollbackEdits.php mass rollback) |
||
| (не показано 39 промежуточных версий 8 участников) | |||
| Строка 1: | Строка 1: | ||
| − | == | + | == Определения == |
{{Определение | {{Определение | ||
|definition = | |definition = | ||
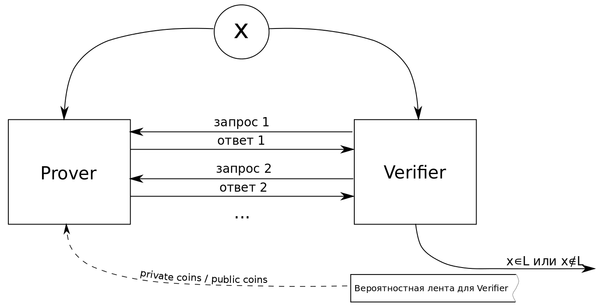
| − | <b>Интерактивным протоколом</b>, разрешающим язык <tex>L</tex>, называется абстрактная машина (см. | + | <b>Интерактивным протоколом</b> (англ. ''interactive protocol'') <tex> \langle P, V \rangle </tex>, разрешающим язык <tex>L</tex>, называется абстрактная машина (см. рисунок), моделирующая вычисления как обмен сообщениями между двумя программами (где <tex>P</tex> означает <tex> \mathrm{Prover}</tex> и <tex> V </tex> означает <tex>\mathrm{Verifier}</tex>), такими, что |
| − | # <tex>P</tex> заинтересован в том, чтобы <tex>V</tex> решил, что слово <tex>x</tex> принадлежит языку | + | # <tex>P</tex> заинтересован в том, чтобы <tex>V</tex> решил, что слово <tex>x</tex> принадлежит языку. |
| − | # <tex>P</tex> не ограничен | + | # <tex>P</tex> не ограничен по времени вычисления и памяти. |
| − | # <tex>V</tex> | + | # <tex>V</tex> заинтересован установить, действительно ли слово <tex>x</tex> принадлежит языку. |
| + | # <tex>V</tex> {{---}} [[Вероятностные вычисления. Вероятностная машина Тьюринга|вероятностная машина Тьюринга]]. | ||
# <tex>V</tex> ограничен полиномиальным временем работы. | # <tex>V</tex> ограничен полиномиальным временем работы. | ||
}} | }} | ||
| + | [[Файл:IPS.png|600px|thumb|right|Схема интерактивного протокола.]] | ||
| − | + | '''Замечания''': | |
| + | # <tex> V </tex> и <tex> P </tex> по очереди становятся активными. <tex> V </tex> активизируется первым. В течение работы <tex> V </tex> выполняет вычисления, используя вход, очередные данные с вероятностной ленты и сообщение, пришедшее от <tex> P </tex>, и пишет запрос <tex> P </tex>. Как только <tex> V </tex> написал сообщение, он дизактивируется, и <tex> P </tex> становится активным, если протокол не завершился. Любая машина может завершить выполнение протокола просто не посылая сообщение во время своей активной фазы. <tex> V </tex> принимает (или отвергает) вход, выводит '''true''' (или '''false''') и завершает выполнение протокола. Время работы <tex> V </tex> {{---}} это сумма времен работы, затраченных <tex> V </tex> в течение активной фазы, и это время ограничено полиномом от длины входа. | ||
| + | # <tex>V</tex>, обменивающийся сообщениями с фиксированным <tex>P</tex>, обозначим <tex>V_{P}</tex>. | ||
| + | # Для того, чтобы <tex> V </tex> принял слово, <tex>P</tex> старается максимизировать вероятность <tex>\mathbb{P}(V_{P}(x) = 1)</tex>, выбирая нужные ответы на запросы. | ||
| + | # Так как мы не ограничиваем <tex>P</tex> в вычислительной мощности, то он может работать бесконечное время, а значит <tex>V</tex> не получит ответ на какой-то вопрос. Но <tex>P</tex> хочет, чтобы <tex> V</tex> принял слово, значит нужно выбирать "хорошие" протоколы, чтобы таких ситуаций не появлялось. | ||
| + | # <tex> P </tex> может быть и вероятностной и детерминированной машиной Тьюринга. Так как он имеет неограниченные вычислительные ресурсы, то на каждом ходу он может выбрать такие вероятностные данные и произвести вычисления с ними, что они максимизируют вероятность принятия слова <tex> V </tex>. | ||
| + | # С другой стороны, для <tex> V </tex> важно быть вероятностной программой, так как иначе он будет принимать или отвергать слова с вероятностью <tex> 1 </tex>. И пользуясь предыдущим фактом, получим, что <tex> V_{P} </tex> всегда принимает слова из <tex> L </tex>. | ||
| + | # Так как <tex> V </tex> может писать и читать полиномиальное число символов, то длина сообщений между <tex> V </tex> и <tex> P </tex> есть полином от длины <tex> x </tex>. | ||
Интерактивные протоколы делятся на два типа в зависимости от доступа <tex>P</tex> к вероятностной ленте <tex>V</tex>: | Интерактивные протоколы делятся на два типа в зависимости от доступа <tex>P</tex> к вероятностной ленте <tex>V</tex>: | ||
| − | # | + | # ''' public coins ''' (русск. ''открытые монеты'') {{---}} <tex>P</tex> может видеть вероятностную ленту <tex>V</tex>; |
| − | # | + | # ''' private coins ''' (русск. ''закрытые монеты''){{---}} <tex>P</tex> <b>не</b> может видеть вероятностную ленту <tex>V</tex>. |
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | + | Если для интерактивного протокола выполняется <tex> \forall x \in L \Rightarrow \exists P : \mathbb{P}(V_{P}(x) = 1) \geqslant c </tex>, то говорят, что он обладает свойством ''' completeness ''' (русск. ''полнота'') равным <tex> c </tex>. | |
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| + | Если <tex>c = 1</tex> ('''perfect completeness''' (русск. ''идеальная полнота'')), то это означает, что никакое верное утверждение не отклоняется <tex> V </tex>. | ||
| − | |||
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | <tex> | + | Если для интерактивного протокола выполняется <tex> \forall x \notin L \Rightarrow \forall P : \mathbb{P}(V_{P}(x) = 1) \leqslant 1 - s </tex>, то говорят, что он обладает свойством ''' soundness ''' (русск. ''достоверность'') равным <tex> s </tex>. |
| − | + | }} | |
| − | + | Если <tex>s = 1 </tex> ('''perfect soundness''' (русск. ''идеальная достоверность'')), то это означет, что если утверждение ложно, то никакой <tex>P</tex> не может убедить <tex>V</tex>, что утверждение истино. В этом случае мы получем класс <tex> \mathrm{NP} </tex>. Потому что <tex> x \in L </tex> тогда и только тогда, если существует последовательность случайных вопросов, генерируемых <tex> V </tex>, и последовательность ответов <tex> P </tex>, которые убеждают <tex> V </tex> в том, что <tex> x \in L </tex>. Обратное утверждение сохраняется по предположению идеальной достоверности. | |
| − | # <tex> | + | |
| − | # число раундов интерактивного протокола <tex> O(f(n)), n = |x| </tex>.< | + | {{Определение |
| + | |definition = | ||
| + | <tex>\mathrm{IP}[f] </tex> (''Interactive Polynomial time'') <tex> = \{L \mid \exists </tex> интерактивный протокол <tex>\langle P, V \rangle : </tex> | ||
| + | # <tex>P</tex> не имеет доступа к вероятностной ленте <tex>V</tex> (private coins). | ||
| + | # <tex> c \geqslant 2/{3} </tex>. | ||
| + | # <tex> s \geqslant 2 /{3} </tex>. | ||
| + | # число раундов интерактивного протокола <tex> O(f(n)), n = |x|\}</tex>. | ||
| + | }} | ||
| + | {{Определение | ||
| + | |definition = <tex>\mathrm{IP}=\bigcup\limits_{p(n) \in poly} \mathrm{IP} [p(n)] </tex> | ||
}} | }} | ||
| + | То есть <tex> \mathrm{IP}</tex> {{---}} множество языков разрешимых интерактивным протоколом, таких, что число сообщений ограничено полиномом от длины слова и <tex>V</tex> должен решить лежит ли слово в языке с вероятностью ошибки не более <tex>1/{3}</tex>. | ||
| − | + | Язык <tex>\mathrm{AM}</tex> (''Arthur–Merlin games'') отличается от <tex>\mathrm{IP}</tex> лишь тем, что <tex>P</tex> может видеть вероятностную ленту <tex>V</tex>. | |
{{Определение | {{Определение | ||
|definition = | |definition = | ||
| − | + | <tex>\mathrm{AM}[f] = \{L \mid \exists </tex> интерактивный протокол <tex>\langle P, V \rangle : </tex> | |
| + | # <tex>P</tex> может читать вероятностную ленту <tex>V</tex> (public coins). | ||
| + | # <tex> c \geqslant 2/{3} </tex>. | ||
| + | # <tex> s \geqslant 2 /{3} </tex>. | ||
| + | # число раундов интерактивного протокола <tex> O(f(n)), n = |x|\}</tex>. | ||
}} | }} | ||
{{Определение | {{Определение | ||
| − | |definition = | + | |definition = <tex>\mathrm{AM}=\bigcup\limits_{p(n) \in poly} \mathrm{AM} [p(n)] </tex> |
| − | + | }} | |
| − | }} | + | |
| + | == Соотношения с другими классами теории сложности == | ||
{{Теорема | {{Теорема | ||
| − | |statement=<tex>\mathrm{BPP} \subset \mathrm{IP[0] | + | |statement=<tex>\mathrm{BPP}</tex> <tex>\subset \mathrm{IP}[0]</tex>. |
|proof= | |proof= | ||
| − | <tex>V</tex> сам по себе является вероятностной машиной Тьюринга и поэтому может разрешить язык из <tex>\mathrm{BPP}</tex> не прибегая к общению с <tex>P</tex>. | + | <tex>V</tex> сам по себе является вероятностной машиной Тьюринга и поэтому может разрешить [[Классы_BPP_и_PP|язык из <tex>\mathrm{BPP}</tex>]] не прибегая к общению с <tex>P</tex>. |
}} | }} | ||
{{Теорема | {{Теорема | ||
| − | |statement=<tex>\mathrm{NP} \subset \mathrm{IP[1] | + | |statement=<tex>\mathrm{NP} \subset \mathrm{IP}[1]</tex>. |
|proof= | |proof= | ||
| − | Для разрешения языка из <tex>\mathrm{NP}</tex> будем использовать следующий протокол: | + | Для разрешения [[Классы_NP_и_Σ₁#.D0.9E.D0.BF.D1.80.D0.B5.D0.B4.D0.B5.D0.BB.D0.B5.D0.BD.D0.B8.D1.8F.2C_.D1.81.D0.B2.D1.8F.D0.B7.D1.8C_.CE.A3.E2.82.81_.D0.B8_NP|языка из <tex>\mathrm{NP}</tex>]] будем использовать следующий протокол: |
| − | <tex>V</tex> будет проверять на принадлежность слова <tex>x</tex> используя сертификат, который он запросит у <tex>P</tex>. Так как <tex>P</tex> не ограничен в вычислительной мощности, он может подобрать подходящий сертификат и именно его и сообщит, так как он заинтересован в том, чтобы <tex>V</tex> принял слово. Для этого требуется лишь один раунд интерактивного протокола. | + | <tex>V</tex> будет проверять на принадлежность слова <tex>x</tex> языку, используя сертификат, который он запросит у <tex>P</tex>. Так как <tex>P</tex> не ограничен в вычислительной мощности, он может подобрать подходящий сертификат и именно его и сообщит, так как он заинтересован в том, чтобы <tex>V</tex> принял слово. Для этого требуется лишь один раунд интерактивного протокола. |
}} | }} | ||
| + | == Язык GNI == | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | <tex>GNI</tex> расшифровывается как Graph Non Isomorphism. Это язык пар неизоморфных друг другу графов. | + | <tex>\mathrm{GNI}</tex> расшифровывается как Graph Non Isomorphism. Это язык пар [[Основные_определения_теории_графов#.D0.9E.D1.80.D0.B8.D0.B5.D0.BD.D1.82.D0.B8.D1.80.D0.BE.D0.B2.D0.B0.D0.BD.D0.BD.D1.8B.D0.B5_.D0.B3.D1.80.D0.B0.D1.84.D1.8B|неизоморфных друг другу графов]]. |
| − | <tex>GNI=\{ \langle G, H \rangle | + | <tex>\mathrm{GNI}=\{ \langle G, H \rangle \mid </tex> графы <tex>G</tex> и <tex>H</tex> не изоморфны <tex>\}</tex>. |
}} | }} | ||
{{Теорема | {{Теорема | ||
| − | |statement=<tex>GNI \in \mathrm{IP[1] | + | |statement=<tex>\mathrm{GNI} \in \mathrm{IP}[1]</tex>. |
|proof= | |proof= | ||
| + | Пусть на вход подали пару графов <tex> \langle G_{0}, G_{1} \rangle </tex> и нужно определить изоморфны ли они. | ||
Будем использовать следующий алгоритм для <tex>V</tex>: | Будем использовать следующий алгоритм для <tex>V</tex>: | ||
| − | # Возьмём случайное число <tex>i \in \{0, 1\}</tex> и случайную перестановку <tex>\pi</tex> с вероятностной ленты; | + | # Возьмём случайное число <tex>i \in \{0, 1\}</tex> и [[Комбинаторные_объекты|случайную перестановку]] <tex>\pi</tex> с вероятностной ленты; |
| − | # Создадим новый граф, перемешав вершины графа c номером <tex>i</tex> перестановкой <tex>\pi</tex> | + | # Создадим новый граф <tex> G </tex>, перемешав вершины графа c номером <tex>i</tex> перестановкой <tex>\pi</tex>. |
| − | # Перешлём <tex>P</tex> полученный граф с просьбой определить, из какого из исходных графов он был получен | + | # Перешлём <tex>P</tex> полученный граф <tex> G </tex> с просьбой определить, из какого из исходных графов он был получен. Если <tex>G_{0} \ncong G_{1} </tex>, то он может перебрать все перестановки графов <tex> G_{0}, G_{1} </tex>, и так как <tex>G_{0} \ncong G_{1} </tex>, то только одна перестановка только на одном графе даст <tex> G </tex>. Иначе, существуют такие перестановки <tex> \phi, \psi </tex>, что <tex> \phi(G_0) = \psi(G_1) = G </tex>, и <tex> P </tex> никак не сможет определить из какого графа был получен <tex> G </tex>. Тогда <tex> P </tex> просто попытается угадать граф, вернув случайно <tex> 0 </tex> или <tex> 1 </tex>. |
| − | # Получив ответ, сравним его с правильным ответом — числом <tex>i</tex> | + | # Получив ответ, сравним его с правильным ответом — числом <tex>i</tex>. |
| − | # Если полученный ответ не совпадёт с <tex>i</tex>, то вернём <tex>0</tex> | + | # Если полученный ответ не совпадёт с <tex>i</tex>, то вернём <tex>0</tex>. |
| − | # Иначе повторим первые пять шагов ещё раз и перейдём к последнему шагу | + | # Иначе повторим первые пять шагов ещё раз и перейдём к последнему шагу. |
# Если мы ещё не вернули <tex>0</tex>, то вернём <tex>1</tex>. | # Если мы ещё не вернули <tex>0</tex>, то вернём <tex>1</tex>. | ||
| − | Покажем, что это удовлетворяет ограничениям на <tex>\mathrm{IP[1] | + | Покажем, что это удовлетворяет ограничениям на <tex>\mathrm{IP}[1]</tex>. |
| − | Во-первых, очевидно, что число раундов не превосходит двух. | + | Во-первых, очевидно, что число раундов не превосходит двух. |
| − | Рассмотрим теперь | + | |
| − | * <tex> \langle G, H \rangle \in GNI</tex>. Тогда <tex>G</tex> и <tex>H</tex> неизоморфны и <tex>P</tex> сможет определить какой граф был перемешан <tex>V</tex>. Таким образом, <tex>P</tex> сможет два раза подряд вернуть правильный ответ и в итоге <tex>V</tex> вернёт 1. | + | Рассмотрим теперь два случая: |
| − | * <tex> \langle G, H \rangle \notin GNI</tex>. Тогда <tex>G</tex> и <tex>H</tex> изоморфны и <tex>P</tex> не сможет определить какой граф был перемешан <tex>V</tex>. Так как <tex>P</tex> заинтересован в том, чтобы <tex>V</tex> принял слово, ему необходимо угадать правильный ответ (иначе <tex>V</tex> просто вернёт <tex>0</tex>). Вероятность того, что <tex>V</tex> примет слово <tex>x</tex>, когда оно не принадлежит языку (то есть <tex>P</tex> два раза подряд верно угадает номер графа), равна <tex> | + | * <tex> \langle G, H \rangle \in \mathrm{GNI}</tex>. Тогда <tex>G</tex> и <tex>H</tex> неизоморфны и <tex>P</tex> сможет определить какой граф был перемешан <tex>V</tex>. Таким образом, <tex>P</tex> сможет два раза подряд вернуть правильный ответ и в итоге <tex>V</tex> вернёт <tex>1</tex>. То есть получили completeness равную <tex> 1 </tex>. |
| + | * <tex> \langle G, H \rangle \notin \mathrm{GNI}</tex>. Тогда <tex>G</tex> и <tex>H</tex> изоморфны и <tex>P</tex> не сможет определить какой граф был перемешан <tex>V</tex>. Так как <tex>P</tex> заинтересован в том, чтобы <tex>V</tex> принял слово, ему необходимо угадать правильный ответ (иначе <tex>V</tex> просто вернёт <tex>0</tex>). Вероятность того, что <tex>V</tex> примет слово <tex>x</tex>, когда оно не принадлежит языку (то есть <tex>P</tex> два раза подряд верно угадает номер графа с вероятностью <tex> 0.5 </tex>), равна <tex>0.25</tex>. Значит soundness равна <tex> 0.75 </tex>, что больше или равно <tex> 2/{3} </tex>. | ||
Таким образом, построенный протокол удовлетворяет условию теоремы. | Таким образом, построенный протокол удовлетворяет условию теоремы. | ||
}} | }} | ||
| + | |||
| + | == См. также == | ||
| + | *[[Вероятностные вычисления. Вероятностная машина Тьюринга]] | ||
| + | *[[Классы NP и Σ₁]] | ||
| + | *[[Классы BPP и PP]] | ||
| + | |||
| + | == Источники информации == | ||
| + | *[[wikipedia: Interactive_proof_system | Wikipedia {{---}} Interactive proof system]] | ||
| + | |||
| + | [[Категория: Теория сложности]] | ||
| + | [[Категория: Вероятностные сложностные классы]] | ||
| + | [[Категория: Интерактивные протоколы]] | ||
Текущая версия на 19:31, 4 сентября 2022
Содержание
Определения
| Определение: |
Интерактивным протоколом (англ. interactive protocol) , разрешающим язык , называется абстрактная машина (см. рисунок), моделирующая вычисления как обмен сообщениями между двумя программами (где означает и означает ), такими, что
|
Замечания:
- и по очереди становятся активными. активизируется первым. В течение работы выполняет вычисления, используя вход, очередные данные с вероятностной ленты и сообщение, пришедшее от , и пишет запрос . Как только написал сообщение, он дизактивируется, и становится активным, если протокол не завершился. Любая машина может завершить выполнение протокола просто не посылая сообщение во время своей активной фазы. принимает (или отвергает) вход, выводит true (или false) и завершает выполнение протокола. Время работы — это сумма времен работы, затраченных в течение активной фазы, и это время ограничено полиномом от длины входа.
- , обменивающийся сообщениями с фиксированным , обозначим .
- Для того, чтобы принял слово, старается максимизировать вероятность , выбирая нужные ответы на запросы.
- Так как мы не ограничиваем в вычислительной мощности, то он может работать бесконечное время, а значит не получит ответ на какой-то вопрос. Но хочет, чтобы принял слово, значит нужно выбирать "хорошие" протоколы, чтобы таких ситуаций не появлялось.
- может быть и вероятностной и детерминированной машиной Тьюринга. Так как он имеет неограниченные вычислительные ресурсы, то на каждом ходу он может выбрать такие вероятностные данные и произвести вычисления с ними, что они максимизируют вероятность принятия слова .
- С другой стороны, для важно быть вероятностной программой, так как иначе он будет принимать или отвергать слова с вероятностью . И пользуясь предыдущим фактом, получим, что всегда принимает слова из .
- Так как может писать и читать полиномиальное число символов, то длина сообщений между и есть полином от длины .
Интерактивные протоколы делятся на два типа в зависимости от доступа к вероятностной ленте :
- public coins (русск. открытые монеты) — может видеть вероятностную ленту ;
- private coins (русск. закрытые монеты)— не может видеть вероятностную ленту .
| Определение: |
| Если для интерактивного протокола выполняется , то говорят, что он обладает свойством completeness (русск. полнота) равным . |
Если (perfect completeness (русск. идеальная полнота)), то это означает, что никакое верное утверждение не отклоняется .
| Определение: |
| Если для интерактивного протокола выполняется , то говорят, что он обладает свойством soundness (русск. достоверность) равным . |
Если (perfect soundness (русск. идеальная достоверность)), то это означет, что если утверждение ложно, то никакой не может убедить , что утверждение истино. В этом случае мы получем класс . Потому что тогда и только тогда, если существует последовательность случайных вопросов, генерируемых , и последовательность ответов , которые убеждают в том, что . Обратное утверждение сохраняется по предположению идеальной достоверности.
| Определение: |
(Interactive Polynomial time) интерактивный протокол
|
| Определение: |
То есть — множество языков разрешимых интерактивным протоколом, таких, что число сообщений ограничено полиномом от длины слова и должен решить лежит ли слово в языке с вероятностью ошибки не более .
Язык (Arthur–Merlin games) отличается от лишь тем, что может видеть вероятностную ленту .
| Определение: |
интерактивный протокол
|
| Определение: |
Соотношения с другими классами теории сложности
| Теорема: |
. |
| Доказательство: |
| сам по себе является вероятностной машиной Тьюринга и поэтому может разрешить язык из не прибегая к общению с . |
| Теорема: |
. |
| Доказательство: |
|
Для разрешения языка из будем использовать следующий протокол: будет проверять на принадлежность слова языку, используя сертификат, который он запросит у . Так как не ограничен в вычислительной мощности, он может подобрать подходящий сертификат и именно его и сообщит, так как он заинтересован в том, чтобы принял слово. Для этого требуется лишь один раунд интерактивного протокола. |
Язык GNI
| Определение: |
| расшифровывается как Graph Non Isomorphism. Это язык пар неизоморфных друг другу графов. графы и не изоморфны . |
| Теорема: |
. |
| Доказательство: |
|
Пусть на вход подали пару графов и нужно определить изоморфны ли они. Будем использовать следующий алгоритм для :
Покажем, что это удовлетворяет ограничениям на . Во-первых, очевидно, что число раундов не превосходит двух. Рассмотрим теперь два случая:
|