|
|
| Строка 13: |
Строка 13: |
| | | | |
| | ===Подсчет подвешенных непомеченных деревьев с порядком на детях=== | | ===Подсчет подвешенных непомеченных деревьев с порядком на детях=== |
| − | Пусть <tex>G_{n}</tex> {{---}} количество деревьев с <tex>n</tex> вершинами, <tex>G_{0} = 1</tex>. <tex>S=Seq(A)</tex> {{---}} множество всех последовательностей из деревьев. <tex>S_{n}</tex> {{---}} количество последовательностей с суммарным количество вершин <tex>n</tex>. Чтобы получить дерево из <tex>n</tex> вершин достаточно взять <tex>1</tex> вершину и подвесить к ней последовательность деревьев с суммарным количеством вершин <tex>n-1</tex>. Тогда <tex>S_{n}=\sum_{i=1}^{n} G_{i} S_{n-1}=C_{n}</tex>, где <tex>C_{n}</tex> {{---}} <tex>n</tex>-ое [[Числа Каталана|число Каталана]], а <tex>G_{n}=S_{n-1}</tex>. | + | Пусть <tex>T_{n}</tex> {{---}} количество деревьев с <tex>n</tex> вершинами, <tex>T_{0} = 1</tex>. <tex>S=Seq(A)</tex> {{---}} множество всех последовательностей из деревьев. <tex>S_{n}</tex> {{---}} количество последовательностей с суммарным количество вершин <tex>n</tex>. Чтобы получить дерево из <tex>n</tex> вершин достаточно взять <tex>1</tex> вершину и подвесить к ней последовательность деревьев с суммарным количеством вершин <tex>n-1</tex>. Тогда <tex>S_{n}=\sum_{i=1}^{n} T_{i} S_{n-1}=C_{n}</tex>, где <tex>C_{n}</tex> {{---}} <tex>n</tex>-ое [[Числа Каталана|число Каталана]], а <tex>T_{n}=S_{n-1}</tex>. |
| | | | |
| − | [[File:Ordered_Rooted_Trees.png|600px]] | + | [[File:Ordered_Rooted_Trees.png|800px]] |
| | | | |
| | ==Множества== | | ==Множества== |
Версия 02:04, 26 декабря 2017
Последовательности
| Утверждение: |
Пусть [math]A=\{a_{1},a_{2}, \ldots ,a_{n}\}[/math] — множество из различных объектов, [math]S=Seq(A)[/math] — множество всех последовательностей из элементов [math]A[/math], [math]W=\{w_{1},w_{2}, \ldots ,w_{m}\}[/math] — количество объектов веса [math]\{1 \ldots m\}[/math]. Тогда количество последовательностей веса [math]n[/math] можно вычислить как [math]S_{n}=\sum_{i=1}^{n} w_{i} S_{n-1}[/math]. |
Подсчет битовых векторов длины [math]n[/math]
Пусть [math]A=\{0, 1\}[/math], [math]W=\{2, 0 \ldots 0\}[/math], [math]S=Seq(A)[/math] — множество всех битовых векторов. Тогда [math]S_{n}=\sum_{i=1}^{n} w_{i} S_{n-1}=2S_{n-1}=2^{n}[/math].
Подсчет Seq из маленьких и больших элементов
Пусть [math]A=\{1, 2\}[/math], [math]W=\{1, 1, 0 \ldots 0\}[/math], [math]S=Seq(A)[/math] — множество всех последовательностей из маленьких и больших элементов [math]S=Seq(A)[/math]. Тогда [math]S_{n}=\sum_{i=1}^{n} w_{i} S_{n-1}=S_{n-1}+S_{n-2}=F_{n}[/math], где [math]F_{n}[/math] — [math]n[/math]-ое число Фибоначчи [1].
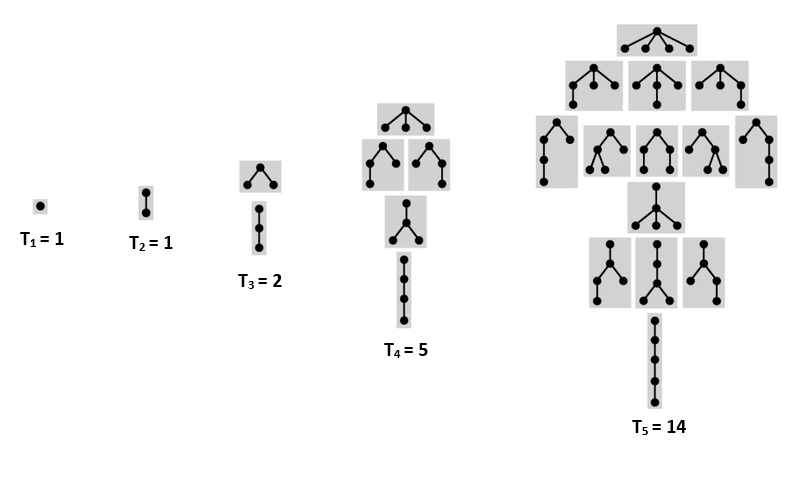
Подсчет подвешенных непомеченных деревьев с порядком на детях
Пусть [math]T_{n}[/math] — количество деревьев с [math]n[/math] вершинами, [math]T_{0} = 1[/math]. [math]S=Seq(A)[/math] — множество всех последовательностей из деревьев. [math]S_{n}[/math] — количество последовательностей с суммарным количество вершин [math]n[/math]. Чтобы получить дерево из [math]n[/math] вершин достаточно взять [math]1[/math] вершину и подвесить к ней последовательность деревьев с суммарным количеством вершин [math]n-1[/math]. Тогда [math]S_{n}=\sum_{i=1}^{n} T_{i} S_{n-1}=C_{n}[/math], где [math]C_{n}[/math] — [math]n[/math]-ое число Каталана, а [math]T_{n}=S_{n-1}[/math].
Множества
| Утверждение: |
Пусть [math]A=\{a_{1},a_{2}, \ldots ,a_{n}\}[/math] — множество из различных объектов, [math]S=PSet(A)[/math] — множество всех множеств объектов, составленных из элементов [math]A[/math], [math]W=\{w_{1},w_{2}, \ldots ,w_{k}\}[/math] — количество объектов веса [math]\{1 \ldots k\}[/math], составленных из элементов [math]A[/math], [math]w_{0} = 1[/math]. Тогда количество множеств из объектов суммарного веса [math]n[/math] можно вычислить как [math]S_{n}=s_{n, n}[/math], где [math]s_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{w_{k}}{i} s_{n-ik, k-1}[/math] — количество таких множеств, что они содержат объекты суммарного веса [math]\leqslant k[/math]. |
Количество PSetиз элементов [math]0[/math] или [math]1[/math]
Пусть [math]A={0, 1}[/math], [math]S=PSet(A)[/math] — множество всех множеств из [math]A[/math], [math]W=\{2, 0 \ldots 0\}[/math], [math]w_{0} = 1[/math]. Тогда [math]S_{n}=s_{n, n}[/math], где [math]s_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} s_{n-ik, k-1}[/math]
- [math]S_{0}=s_{0, 0} = 1[/math]
- [math]S_{1}=s_{1, 1} = s_{1, 0} + 2s_{0, 0} = 2s_{0, 0} = 2[/math]
- [math]S_{2}=s_{2, 2} = s_{2, 1} + 0 \times s_{0, 1} = s_{2, 0} + 2s_{1, 0} + s_{0, 0}= s_{0, 0} = 1[/math]
- [math]S_{3}=s_{3, 3} = s_{3, 2} + 0 \times s_{0, 2} = s_{3, 1} + 0 \times s_{0, 1} = s_{3, 0} + 2s_{2, 0} + 0 \ times s_{1, 0} + 0 \ times s_{0, 0}= 0[/math]
- Для [math]n \gt 2[/math], [math]S_{n} = 0[/math]
- [math]\{\}[/math]
- [math]\{0\}, \{1\}[/math]
- [math]\{0, 1\}[/math]
Количество разбиений на слагаемые
Пусть [math]A=\mathbb{N}[/math], [math]S=PSet(A)[/math] — множество всех разбиений на слагаемые, [math]W=\{1 \ldots 1\}[/math], [math]w_{0} = 1[/math]. Тогда [math]S_{n}=s_{n, n}[/math], где [math]s_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} s_{n-ik, k-1} = s_{n, k-1} + s_{n - k, k}[/math], что, как не сложно заметить, соответсвует формуле, полученной методом динамического программирования.
| Утверждение: |
Пусть [math]A=\{a_{1},a_{2}, \ldots ,a_{n}\}[/math] — множество из различных объектов, [math]S=MSet(A)[/math] — множество всех мультимножеств объектов, составленных из элементов [math]A[/math], [math]W=\{w_{1},w_{2}, \ldots ,w_{k}\}[/math] — количество объектов веса [math]\{1 \ldots k\}[/math], составленных из элементов [math]A[/math], [math]w_{0} = 1[/math]. Тогда количество мультимножеств из объектов суммарного веса [math]n[/math] можно вычислить как [math]S_{n}=s_{n, n}[/math], где [math]s_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} \binom{w_{k}+i-1}{i} s_{n-ik, k-1}[/math] — количество таких мультимножеств, что они содержат объекты суммарного веса [math]\leqslant k[/math]. |
Количество MSet из элементов [math]0[/math] или [math]1[/math]
Пусть [math]A={0, 1}[/math], [math]S=PSet(A)[/math] — множество всех множеств из [math]A[/math], [math]W=\{2, 0 \ldots 0\}[/math], [math]w_{0} = 1[/math]. Тогда [math]S_{n}=s_{n, n}[/math], где [math]s_{n, k}=\sum_{i=0}^{\lfloor \frac{n}{k} \rfloor} s_{n-ik, k-1}[/math]
- [math]S_{0}=s_{0, 0} = 1[/math]
- [math]S_{1}=s_{1, 1} = s_{1, 0} + 2s_{0, 0} = 2s_{0, 0} = 2[/math]
- [math]S_{2}=s_{2, 2} = s_{2, 1} + 0 \times s_{0, 1} = s_{2, 0} + 2s_{1, 0} + 3s_{0, 0}= 3s_{0, 0} = 3[/math]
- [math]S_{3}=s_{3, 3} = s_{3, 2} + 0 \times s_{0, 2} = s_{3, 1} + 0 \times s_{0, 1} = s_{3, 0} + 2s_{2, 0} + 3s_{1, 0} + 4s_{0, 0}= 4s_{0, 0} = 4[/math]
- [math]\{\}[/math]
- [math]\{0\}, \{1\}[/math]
- [math]\{0, 0\}, \{0, 1\}, \{1, 1\}[/math]
- [math]\{0, 0, 0\}, \{0, 0, 1\}, \{0, 1, 1\}, \{1, 1, 1\}[/math]
- [math]{S_{n}=s_{n, n} = s_{n, n-1} + 0 \times s_{0, n-1} = s_{n, n-2} + 0 \times s_{0, n-2} = \ldots = s_{n, 0} + 2s_{n - 1, 0} + \ldots + ns_{1, 0} + (n+1) s_{0,0} = (n + 1) s_{0,0} = n+1}[/math]
Примeчания
