Красно-чёрное дерево (удалить) — различия между версиями
м (Дмитрий Мурзин переименовал страницу Красно- черное дерево в Красно-чёрное дерево) |
м (Дмитрий Мурзин переименовал страницу Красно-чёрное дерево в Красно-чёрное дерево (удалить): Статью нужно удалить, так как существует…) |
(нет различий)
| |
Версия 23:59, 31 января 2019
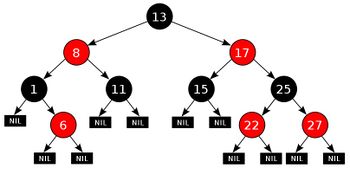
- Все листья дерева чёрные.
- Корень дерева чёрный.
- Все сыновья красного узла чёрные.
- На каждой ветви дерева, идущей от корня к листу, число чёрных узлов одно и то же.
При этом все листья дерева являются фиктивными и не содержат данных. Число чёрных узлов между корнем и узлом называется чёрной высотой дерева.
Свойства
- Свойство 1: Число листьев в дереве с чёрной высотой не менее, чем .
Доказательство: Докажем по индукции. При получаем дерево, в котором чёрными являются только листья, а их больше одного.
Иначе пусть корень - чёрный, тогда оба его поддерева имеют чёрную высоту h-1 и, следовательно, не менее, чем элементов. Тогда всё дерево имеет более элементов. В случае, если корень красный, то оба его поддерева имеют чёрные корни и чёрную высоту , то есть, как только что было показано, не менее элементов. Таким образом, дерево будет иметь более элементов.
- Свойство 2: Число листьев в красно-чёрном дереве высоты не менее .
Доказательство: Возьмём самый длинный путь в дереве. Всего в нём узлов. По крайней мере половина узлов чёрные, поскольку двух подряд идущих красных узлов быть не может, а лист чёрный. Поэтому чёрная высота дерева не меньше , и, по первому утверждению, элементов.
Отсюда также получаем, что высота дерева не более , где N - число элементов дерева, т.е.
Операции
- Вставка элемента. Каждый элемент вставляется вместо листа, поэтому для выбора места вставки идём от корня до тех пор, пока указатель на следующего сына не станет nil(т.е. этот сын - лист). Вставляем вместо него новый элемент с nil-потомками и красным цветом. Теперь проверяем балансировку. Если отец нового элемента красный, то достаточно рассмотреть только два случая:
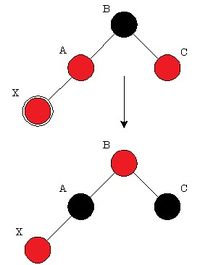
1. "Дядя" этого узла тоже красный. Тогда просто перекрашиваем "отца" и "дядю" в чёрный цвет, а "деда" - в красный. Проверяем, не нарушает ли он теперь балансировку. Если в результате этих перекрашиваний мы дойдём до корня, то в нём в любом случае ставим чёрный цвет.
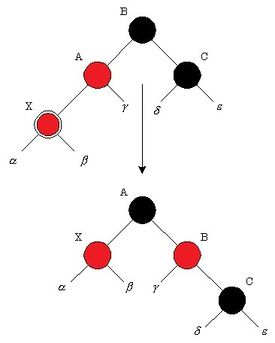
2. "Дядя" чёрный. Если выполнить только перекрашивание, то может нарушиться постоянство чёрной высоты дерева по всем ветвям. Поэтому выполняем поворот. Если добавляемый узел был правым потомком, то необходимо сначала выполнить левое вращение, которое сделает его левым потомком.
- Удаление вершины.При удалении вершины могут возникнуть три случая в зависимости от количества её детей:
- Если у вершины нет детей, то изменяем указатель на неё у родителя на nil.
- Если у неё только один ребёнок, то делаем у родителя ссылку на него вместо этой вершины.
- Если же имеются оба ребёнка, то находим вершину со следующим значением ключа. У такой вершины нет левого ребёнка. Удаляем уже эту вершину описанным во втором пункте способом, скопировав её ключ в изначальную вершину.
Проверим балансировку дерева. Т.к. при удалении красной вершины свойства дерева не нарушаются, то восстановление балансировки потребуется только при удалении чёрной. Рассмотрим ребёнка удалённой вершины.
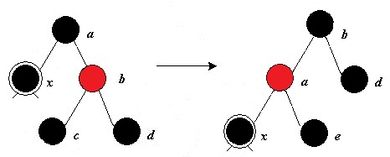
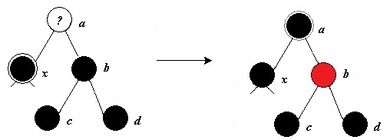
1. Если брат этого ребёнка красный, то делаем вращение вокруг ребра между отцом и братом, тогда брат становится родителем отца. Красим его в чёрный, а отца - в красный цвет.
2. Если брат текущей вершины был чёрным, то получаем три случая:
- Оба ребёнка у брата чёрные. Красим брата в красный цвет и рассматриваем далее отца вершины.
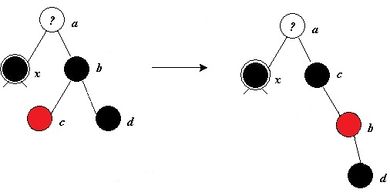
- Если у брата правый ребёнок чёрный,а левый красный, то перекрашиваем брата и его левого сына и делаем вращение.
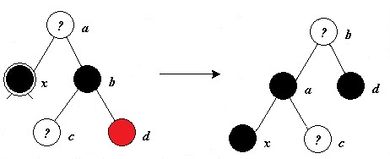
- В же у брата правый ребёнок красный, то перекрашиваем брата в цвет отца, его ребёнка и отца - в чёрный, делаем вращение и выходим из алгоритма.
Продолжаем тот же алгоритм, пока текущая вершина чёрная и мы не дошли до корня дерева. При удалении выполняется не более трёх вращений.
- Объединение красно-чёрных деревьев. Объединение двух красно-чёрных деревьев и по элементу x выполняется, когда и .
Найдём чёрные высоты деревьев. Предположим также, что . Тогда в дереве ищем среди чёрных вершин, имеющих чёрную высоту , вершину y с наибольшим ключом. Пусть — поддерево с корнем y. Объединяем это дерево с в одно с красным корнем x. Теперь родителем вершины x становится бывший отец вершины y. Осталось восстановить свойства красно-черного дерева, чтобы у красной вершины не было красных детей. Делается аналогично алгоритму добавления вершины.
Т.к. общее время выполнения каждой из операций порядка высоты дерева ,то все они выполняются за .