Кратчайший путь в ациклическом графе — различия между версиями
IRomchig (обсуждение | вклад) (→Решение) |
IRomchig (обсуждение | вклад) (→Пример) |
||
| Строка 36: | Строка 36: | ||
| '''4''' || - || - || - || 0 | | '''4''' || - || - || - || 0 | ||
|} | |} | ||
| − | Требуется найти путь из ''' | + | Требуется найти путь из '''2''' в '''4'''. |
Матрица p будет выглядеть следующим образом: <br /> | Матрица p будет выглядеть следующим образом: <br /> | ||
{| class="wikitable" cellpadding="4" border="1" style="border-collapse: collapse;" | {| class="wikitable" cellpadding="4" border="1" style="border-collapse: collapse;" | ||
| Строка 53: | Строка 53: | ||
Ответ равен 2. | Ответ равен 2. | ||
| + | |||
==Источники== | ==Источники== | ||
* [http://en.wikipedia.org/wiki/Optimal_substructure Принцип оптимальности на подзадаче (в качестве примера разбирается задача поиска кратчайшего пути в ациклическом графе)(англ.)] | * [http://en.wikipedia.org/wiki/Optimal_substructure Принцип оптимальности на подзадаче (в качестве примера разбирается задача поиска кратчайшего пути в ациклическом графе)(англ.)] | ||
[[Категория: Динамическое программирование ]] | [[Категория: Динамическое программирование ]] | ||
Версия 09:01, 29 ноября 2011
Формулировка задачи
Пусть дан ациклический взвешенный граф. Требуется найти вес кратчайшего пути из u в v
| Определение: |
| Кратчайший путь из u в v – это такой путь из u в v, что его вес меньше или равен веса любого другого пути из u в v |
Решение
Пусть d — матрица, где d[i] — вес кратчайшего пути из u в i. Изначально значения d равны бесконечности, кроме d[u], который равен 0. Пусть w[i][j] - вес ребра из i в j. Будем обходить граф в порядке топологической сортировки. Получаем следующие соотношения:
Так как мы обходим граф в порядке топологической сортировки, то на i-ом шаге во всех d[j] (j такие, что: существует ребро из j в i) уже записаны оптимальные ответы, и следовательно в d[i] также будет записан оптимальный ответ.
Реализация
Реализуем данный алгоритм методом "динамика вперед":
//d, w - матрицы как в описании, p - массив индексов вершин графа в порядке топологической сортировки, i, j - счетчики
inputData() //считывание данных
for i = 1 to n d[i] = infinity
p = topSort() //топологическая сортировка
d[p[u]] = 0
for i = 1 to n for j: d[j] = min(d[j], d[p[i]] + w[p[i]][j])
writeData(); // запись данных
Пример
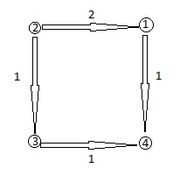
Пусть дан граф со следующими весами w ребер:
| 1 | 2 | 3 | 4 | |
| 1 | 0 | - | - | 1 |
| 2 | 2 | 0 | 1 | - |
| 3 | - | - | 0 | 1 |
| 4 | - | - | - | 0 |
Требуется найти путь из 2 в 4.
Матрица p будет выглядеть следующим образом:
| 1 | 2 | 3 | 4 |
| 2 | 1 | 3 | 4 |
Матрица d будет выглядеть следующим образом:
| 1 | 2 | 3 | 4 |
| 1 | 0 | 2 | 2 |
Ответ равен 2.