К-d деревья и перечисление точек в произвольном прямоугольнике (статика) — различия между версиями
Gromak (обсуждение | вклад) (Новая страница: «{{ptready}} == Определение и построение == '''K-d дерево''' (short for k-dimensional tree) {{---}} статическая структ...») |
Gromak (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
{{ptready}} | {{ptready}} | ||
| + | |||
== Определение и построение == | == Определение и построение == | ||
| + | [[Файл:Kd-tree.png | 500px | thumb | Пример]] | ||
| + | |||
'''K-d дерево''' (short for k-dimensional tree) {{---}} статическая структура данных для хранения точек в <tex>k</tex>-мерном пространстве. Позволяет отвечать на запрос, какие точки лежат в данном прямоугольнике. | '''K-d дерево''' (short for k-dimensional tree) {{---}} статическая структура данных для хранения точек в <tex>k</tex>-мерном пространстве. Позволяет отвечать на запрос, какие точки лежат в данном прямоугольнике. | ||
| − | ''Примечание: в книжке описывается двумерный вариант, и на лекциях, кажется, только он был, поэтому далее считается, что <tex>k = 2</tex>. Обобщение на большую размерность достаточно просто додумать при необходимости.'' | + | ''Примечание: в книжке описывается двумерный вариант, и на лекциях, кажется, только он был, поэтому далее считается, что <tex>k = 2</tex>. Обобщение на большую размерность достаточно просто додумать при необходимости. Местами будет упомянут и случай <tex>k > 2</tex>.'' |
Строится это дерево следующим образом: разобьём все точки вертикальной прямой так, чтобы слева (нестрого) и справа (строго) от неё было примерно поровну точек (для этого посчитаем медиану первых координат). Получим подмножества для левого и правого ребёнка. Далее построим для этих подмножеств деревья, но разбивать будем уже не вертикальной, а горизонтальной прямой (для этого посчитаем медиану вторых координат). И так далее (раз считаем, что <tex>k = 2</tex>, то на следующем уровне вновь будем разбивать вертикальными прямыми). | Строится это дерево следующим образом: разобьём все точки вертикальной прямой так, чтобы слева (нестрого) и справа (строго) от неё было примерно поровну точек (для этого посчитаем медиану первых координат). Получим подмножества для левого и правого ребёнка. Далее построим для этих подмножеств деревья, но разбивать будем уже не вертикальной, а горизонтальной прямой (для этого посчитаем медиану вторых координат). И так далее (раз считаем, что <tex>k = 2</tex>, то на следующем уровне вновь будем разбивать вертикальными прямыми). | ||
| Строка 9: | Строка 12: | ||
''Замечание: проблемы могут возникнуть, если много точек имеют одинаковую координату, тогда разбить примерно поровну не получится (почти все точки будут лежать на медиане и попадут в левую часть). Лучший способ борьбы с этим {{---}} не вспоминать о данной проблеме совсем. Но вообще с этим борются, используя composite numbers, то есть сравнивая ещё и по другой (другим) координате. Не думаю, что об этом нужно много писать.'' | ''Замечание: проблемы могут возникнуть, если много точек имеют одинаковую координату, тогда разбить примерно поровну не получится (почти все точки будут лежать на медиане и попадут в левую часть). Лучший способ борьбы с этим {{---}} не вспоминать о данной проблеме совсем. Но вообще с этим борются, используя composite numbers, то есть сравнивая ещё и по другой (другим) координате. Не думаю, что об этом нужно много писать.'' | ||
| − | + | Реализовывать построение можно рекурсивно с помощью функции <tex>BuildKdTree(P, Depth)</tex>, принимающей множество точек и глубину. В зависимости от остатка при делении на размерность (в нашем случае от чётности) сплитим множество на два подмножества и делаем рекурсивные вызовы. Для лучшего понимания приведём псевдокод: | |
<code> | <code> | ||
| Строка 27: | Строка 30: | ||
</code> | </code> | ||
| + | {{Лемма | ||
| + | |about= | ||
| + | О времени построения | ||
| + | |statement= | ||
| + | Построение выполняется за <tex>O(n \log n)</tex>. | ||
| + | |proof= | ||
| + | Время построения обозначим <tex>T(n)</tex>. Поиск медианы можно сделать за линейное время, поэтому достаточно очевидно, что: | ||
| + | |||
| + | <tex>T(n) = O(1)</tex> if <tex>n = 1</tex>. | ||
| + | |||
| + | <tex>T(n) = O(n) + 2 \cdot T(n / 2)</tex>, otherwise. | ||
| + | |||
| + | Умные люди могут сразу же заметить, что решением этого является <tex>T(n) = O(n \log n)</tex>. А люди моего уровня могут почитать умные книжки или просто поверить в данный факт. | ||
| + | |||
| + | Также стоит отметить, что можно и не искать медиану за линейное время, а просто посортить все точки в самом начале и дальше использовать это. В реализации попроще, асимптотика та же. | ||
| + | }} | ||
| + | {{Лемма | ||
| + | |about= | ||
| + | О занимаемой памяти | ||
| + | |statement= | ||
| + | K-d дерево требует <tex>O(n)</tex> памяти. | ||
| + | |proof= | ||
| + | Высота дерева, очевидно, логарифмическая, а листьев всего <tex>O(n)</tex>. Поэтому будет <tex>O(n)</tex> вершин, каждая занимает <tex>O(1)</tex> памяти. | ||
| + | }} | ||
| + | == Запрос == | ||
| + | Ы | ||
== Ссылки == | == Ссылки == | ||
Версия 13:20, 20 января 2014
| Конспект написан не до конца, но основные вещи уже есть. |
Определение и построение
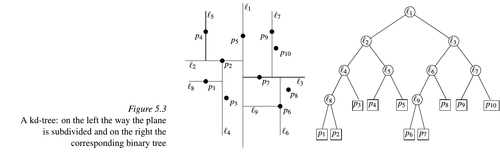
K-d дерево (short for k-dimensional tree) — статическая структура данных для хранения точек в -мерном пространстве. Позволяет отвечать на запрос, какие точки лежат в данном прямоугольнике.
Примечание: в книжке описывается двумерный вариант, и на лекциях, кажется, только он был, поэтому далее считается, что . Обобщение на большую размерность достаточно просто додумать при необходимости. Местами будет упомянут и случай .
Строится это дерево следующим образом: разобьём все точки вертикальной прямой так, чтобы слева (нестрого) и справа (строго) от неё было примерно поровну точек (для этого посчитаем медиану первых координат). Получим подмножества для левого и правого ребёнка. Далее построим для этих подмножеств деревья, но разбивать будем уже не вертикальной, а горизонтальной прямой (для этого посчитаем медиану вторых координат). И так далее (раз считаем, что , то на следующем уровне вновь будем разбивать вертикальными прямыми).
Замечание: проблемы могут возникнуть, если много точек имеют одинаковую координату, тогда разбить примерно поровну не получится (почти все точки будут лежать на медиане и попадут в левую часть). Лучший способ борьбы с этим — не вспоминать о данной проблеме совсем. Но вообще с этим борются, используя composite numbers, то есть сравнивая ещё и по другой (другим) координате. Не думаю, что об этом нужно много писать.
Реализовывать построение можно рекурсивно с помощью функции , принимающей множество точек и глубину. В зависимости от остатка при делении на размерность (в нашем случае от чётности) сплитим множество на два подмножества и делаем рекурсивные вызовы. Для лучшего понимания приведём псевдокод:
BuildKdTree(P, Depth) //Input. A set of points P and the current depth Depth. //Output. The root of a kd-tree storing P. if P contains only one point return a leaf storing this point else if depth is even Split P into two subsets and with a vertical line through the median x-coordinate of the points in P else Split P into two subsets and with a horizontal line through the median y-coordinate of the points in P. <- BuildKdTree(, Depth + 1) <- BuildKdTree(, Depth + 1) Create a node v storing , make the left child of v, and make the right child of v. return v
| Лемма (О времени построения): |
Построение выполняется за . |
| Доказательство: |
|
Время построения обозначим . Поиск медианы можно сделать за линейное время, поэтому достаточно очевидно, что: if . , otherwise. Умные люди могут сразу же заметить, что решением этого является . А люди моего уровня могут почитать умные книжки или просто поверить в данный факт. Также стоит отметить, что можно и не искать медиану за линейное время, а просто посортить все точки в самом начале и дальше использовать это. В реализации попроще, асимптотика та же. |
| Лемма (О занимаемой памяти): |
K-d дерево требует памяти. |
| Доказательство: |
| Высота дерева, очевидно, логарифмическая, а листьев всего . Поэтому будет вершин, каждая занимает памяти. |
Запрос
Ы
Ссылки
- van Kreveld, de Berg, Overmars, Cheong — Computational Geometry. Algorithms and Applications. Страница 99.
- Английская Википедия
- Русская Википедия