Левосторонние красно-чёрные деревья — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
(→‎Удаление)
м (rollbackEdits.php mass rollback)
 
(не показано 155 промежуточных версий 6 участников)
Строка 1: Строка 1:
 
{{Определение
 
{{Определение
−
|definition =  Left-leaning Red-Black Trees {{---}} модификация [[Красно-черное дерево|красно-черных деревьев]], имеющая ряд преимуществ на классической структурой. Разработана Робертом Соджевиском в 2008 году.
+
|definition =  Левостороннее красно-черное дерево {{---}} тип сбалансированного двоичного дерева поиска, гарантирующий такую же асимптотическую сложность операций, как у красно-черного дерева поиска.
 
   }}
 
   }}
−
==Преимущества==
+
 
−
* необходимо менее 80 строчек кода для реализации структуры
+
==Свойства==
−
* более быстрая вставка, удаление элементов
+
*Корневой узел всегда черный.
−
* простота
+
*Каждый новый узел всегда окрашен в красный цвет.
 +
*Каждый дочерний нулевой узел листа дерева считается черным.
 +
 
 
==Вращения==
 
==Вращения==
−
Чтобы поддерживать красно-черные двоичное деревья поиска необходимо соблюдать следующие инвариантные свойства при вставке и удалении:
+
Чтобы поддерживать левосторонние красно-черные двоичные деревья поиска необходимо соблюдать следующие инварианты при вставке и удалении:
−
* Ни один обход от корня до листьев дерева не содержит двух последовательных красных узлов.
+
* Ни один путь от корня до листьев дерева не содержит двух последовательных красных узлов.
 
* Количество черных узлов на каждом таком пути одинаково.
 
* Количество черных узлов на каждом таком пути одинаково.
−
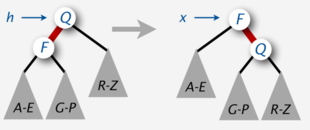
Из этих инвариантов следует, что длина каждого пути от корня до листьев в красно-черном дереве с <tex>N</tex> узлами не превышает <tex>2 \cdot log(N)</tex> .
 
  
−
Основные операции, используемые алгоритмами сбалансированного дерева для поддержания баланса при вставке и удалении, называются вращениями. Эти операции трансформируют <tex>3</tex>-узел,левый потомок которого окрашен в красный, в  <tex>3</tex>-узел, правый потомок которого окрашен в красный и наоборот.  Вращения сохраняют два указанных выше инварианта, не изменяют поддеревья узла.
+
Основные операции, используемые алгоритмами сбалансированного дерева для поддержания баланса при вставке и удалении, называются вращением вправо и вращением влево. Первая операция трансформируют <tex>3</tex>-узел (совокупность из <tex>3</tex> узлов, где <tex>2</tex> узла являются наследниками третьего, причем одна из связей является красной), левый потомок которого окрашен в красный, в  <tex>3</tex>-узел, правый потомок которого окрашен в красный,вторая операция {{---}} наоборот.  Вращения сохраняют два указанных выше инварианта, не изменяют поддеревья узла.
−
===Псевокод===
+
===Псевдокод===
 
[[File:rotateRight.png|310px|thumb|upright|Rotate Right]]
 
[[File:rotateRight.png|310px|thumb|upright|Rotate Right]]
−
   '''Node''' rotateRight( h : '''Node''') :
+
   '''Node''' rotateRight(h : '''Node''')  
 
       x = h.left
 
       x = h.left
−
       h.left= x.right
+
       h.left = x.right
−
       x.right= h
+
       x.right = h
 
       x.color = h.color
 
       x.color = h.color
 
       h.color = RED
 
       h.color = RED
−
    '''return''' x
+
      '''return''' x
 
[[File:rotateLeft.png|310px|thumb|upright|Rotate Left]]
 
[[File:rotateLeft.png|310px|thumb|upright|Rotate Left]]
−
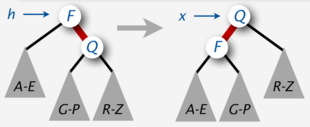
   '''Node''' rotateLeft( h : '''Node''') :
+
   '''Node''' rotateLeft(h : '''Node''')  
 
       x = h.right
 
       x = h.right
 
       h.right = x.left
 
       h.right = x.left
Строка 29: Строка 30:
 
       x.color = h.color
 
       x.color = h.color
 
       h.color = RED
 
       h.color = RED
−
  '''return''' x
+
      '''return''' x
  
 
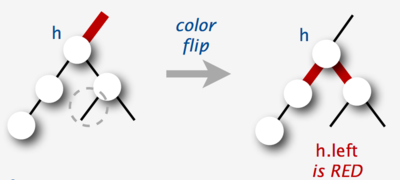
==Переворот цветов==
 
==Переворот цветов==
−
 
+
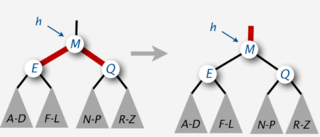
В красно-черных деревьях используется такая  операция как '''переворот цветов''' , которая инвертирует цвет узла и двух его детей.  Она не изменяет количество черных узлов  на любом пути от корня до листа, но может привести к появлению двух последовательных красных узлов.
−
В красно-черных деревьях используется такая  операция как <tex>color flip</tex>, которая инвертирует цвет узла и двух его детей.  Она не изменяет количество черных узлов  при любом обходе от корня до листьев дерева, но может привести к появлению двух последовательных красных узлов.  
+
===Псевдокод===
−
[[File: ColorFlip.png|320px|thumb|upright| Color Flip]]
+
[[File: ColorFlip.png|320px|thumb|upright| Переворот цветов]]
−
 
+
   '''void''' flipColors(h : '''Node''' h)  
−
   '''void''' flipColors( h : '''Node''' h) :
 
 
       h.color = '''!''' h.color
 
       h.color = '''!''' h.color
−
       h.left.color = '''!''' h.left.color
+
       h.left.color = '''!''' h.left.color
−
       h.right.color = <tex> !</tex> h.right.color
+
       h.right.color = '''!''' h.right.color
−
 
 
  
 
==Вставка==
 
==Вставка==
−
Вставка в LLRB базируется на <tex>4</tex> простых операциях:
+
Вставка в ЛСКЧД базируется на <tex>4</tex> простых операциях:
  
 
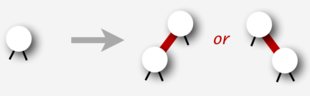
*Вставка нового узла к листу дерева:
 
*Вставка нового узла к листу дерева:
 +
Если высота узла  нулевая, возвращаем новый красный узел.
 
[[File:insertNode.png|310px|thumb|upright|Вставка нового узла]]
 
[[File:insertNode.png|310px|thumb|upright|Вставка нового узла]]
−
 
−
  if (h == null)
 
−
      return new Node(key, value, RED);
 
−
 
 
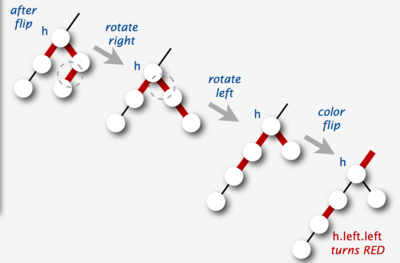
*Расщепление узла с <tex>4</tex>-я потомками:
 
*Расщепление узла с <tex>4</tex>-я потомками:
 +
Если левый предок и правый предок  красные, запускаем переворот цветов от текущего узла.
 
[[File:Split4node.png|310px|thumb|upright|Расщепление узла]]
 
[[File:Split4node.png|310px|thumb|upright|Расщепление узла]]
−
  if (isRed(h.left) && isRed(h.right))
 
−
      colorFlip(h);
 
−
 
 
*Принудительное вращение влево:
 
*Принудительное вращение влево:
 
[[File:Enforce.png|310px|thumb|upright|Принудительное вращение]]
 
[[File:Enforce.png|310px|thumb|upright|Принудительное вращение]]
−
  if (isRed(h.right))
+
Если правый предок красный, вращаем текущую вершину влево.
−
      h = rotateLeft(h);
 
−
 
 
 
*Балансировка узла с <tex>4</tex>-я потомками:
 
*Балансировка узла с <tex>4</tex>-я потомками:
 
[[File:Balance4node.png|310px|thumb|Балансировка]]
 
[[File:Balance4node.png|310px|thumb|Балансировка]]
−
  if (isRed(h.left) && isRed(h.left.left))
+
Если левый предок красный и левый предок левого предка красный, то вращаем текущую вершину вправо.
−
      h = rotateRight(h);
+
 
 
    
 
    
 
===Псевдокод===
 
===Псевдокод===
−
   '''void''' insert( '''key''' : Key, '''value''' : Value ):
+
   '''void''' insert(key : '''Key''', value : '''Value''' )  
 
         root = insert(root, key, value)
 
         root = insert(root, key, value)
 
         root.color = BLACK
 
         root.color = BLACK
  
  
−
   '''Node''' insert( h : '''Node''', key : '''Key''', value : '''Value'''):
+
   '''Node''' insert(h : '''Node''', key : '''Key''', value : '''Value''')
−
      //Вставка нового узла к листу дерева
+
      <span style="color:#008000">// Вставка нового листа</span>
 
       '''if''' h == ''null''     
 
       '''if''' h == ''null''     
 
           '''return''' '''new''' Node(key, value)
 
           '''return''' '''new''' Node(key, value)
−
      //Расщепление узла с <tex>4</tex>-я потомками
+
      <span style="color:#008000">// Расщепление узла с <tex>4</tex>-я потомками</span>
 
       '''if''' isRed(h.left) '''&&''' isRed(h.right)
 
       '''if''' isRed(h.left) '''&&''' isRed(h.right)
 
           colorFlip(h)
 
           colorFlip(h)
−
      //Стандартная вставка [[Дерево поиска, наивная реализация|в дереве поиска]]
+
      <span style="color:#008000">// Стандартная вставка [[Дерево поиска, наивная реализация|в дереве поиска]]</span>
−
       '''int''' cmp = key.compareTo(h.key)
+
       '''if''' key = h.key  
−
      '''if'''  cmp == 0
 
 
           h.val = value
 
           h.val = value
 
       '''else'''  
 
       '''else'''  
−
           '''if''' cmp < 0
+
           '''if''' key < h.key 
 
               h.left = insert(h.left, key, value)   
 
               h.left = insert(h.left, key, value)   
 
           '''else'''  
 
           '''else'''  
 
               h.right = insert(h.right, key, value)
 
               h.right = insert(h.right, key, value)
−
          //Принудительное вращение влево
+
          <span style="color:#008000">// Принудительное вращение влево</span>
−
           '''if''' isRed(h.right) '''&&''' '''!'''isRed(h.left)  
+
           '''if''' isRed(h.right) '''&&''' '''!'''isRed(h.left)
−
            h = rotateLeft(h)
+
              h = rotateLeft(h)
−
          ////Балансировка узла с <tex>4</tex>-я потомками
+
          <span style="color:#008000">// Балансировка узла с <tex>4</tex>-я потомками</span>
 
           '''if''' isRed(h.left) '''&&''' isRed(h.left.left)
 
           '''if''' isRed(h.left) '''&&''' isRed(h.left.left)
−
            h = rotateRight(h)
+
              h = rotateRight(h)
−
       '''return''' ''h''
+
       '''return''' h
  
 +
==Поиск==
 +
Поиск в левосторонних красно-черных деревьях эквивалентен поиску в [[Дерево поиска, наивная реализация|наивной реализации дерева поиска]].
 +
Для поиска элемента в красно-черных деревьях дереве поиска можно воспользоваться циклом,который проходит от корня до искомого элемента. Если же элемент отсутствует, цикл пройдет до листа дерева и прервется. Для каждого узла цикл сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае цикл повторяет для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы <tex>O(h)</tex>, где <tex>h</tex> {{---}} высота дерева.
 +
===Псевдокод===
 +
'''Value''' search(key : '''Key''')
 +
    '''Node''' x = root
 +
    '''while''' (x '''!'''= null)
 +
      '''if''' key = x.key
 +
          '''return''' x.val
 +
      '''else'''
 +
          '''if''' key < x.key
 +
              x = x.left
 +
      '''else'''
 +
          '''if''' key > x.key
 +
              x = x.right
 +
    '''return''' ''null''
  
−
  '''Value''' search(key : '''Key'''):
+
==Исправление правых красных связей==
−
    '''Node''' x = root
+
*Использование Переворота цветов и вращений сохраняет баланс черной связи.
−
    '''while''' x '''!'''= null
+
*После удаления необходимо исправить правые красные связи и устранить узлы с <tex>4</tex>-я потомками
−
      '''int''' cmp = key.compareTo(x.key)
+
      <span style="color:#008000">// Исправление правых красных связей</span>
−
      '''if''' cmp == 0
+
  '''Node''' fixUp(h : '''Node''')
−
        '''return''' x.val
+
      '''if''' isRed(h.right) 
−
      '''else'''
+
          h = rotateLeft(h) 
−
        '''if''' cmp < 0
+
      <span style="color:#008000">// Вращение <tex>2</tex>-ой красной пары пары</span>
−
          x = x.left
+
      '''if''' isRed(h.left) '''&&''' isRed(h.left.left)
−
        '''else'''  
+
          h = rotateRight(h) 
−
          '''if''' cmp > 0
+
      <span style="color:#008000">// Балансировка узла с <tex>4</tex>-я потомками</span>
−
            x = x.right
+
      '''if''' isRed(h.left) '''&&''' isRed(h.right)
−
  '''return''' ''null''
+
          colorFlip(h)  
−
==Удаление==
+
      '''return''' h
−
*Использование <tex>flipColor</tex> и <tex>rotate</tex>  сохраняют баланс черной связи.
 
−
* Необходимо исправить правые красные связи и устранить узлы с <tex>4-</tex>я потомками
 
  
−
  '''Node''' fixUp(h : '''Node'''){
+
==Удаление максимума==
−
      '''if''' (isRed(h.right))
+
* Спускаемся вниз по правому краю  дерева.
−
          h = rotateLeft(h);
+
* Если поиск заканчивается на узле с <tex>4</tex>-мя или <tex>5</tex>-ю потомками, просто удаляем узел.
−
      '''if''' (isRed(h.left) '''&&''' isRed(h.left.left))
 
−
          h = rotateRight(h);
 
−
      '''if''' (isRed(h.left) '''&&''' isRed(h.right))
 
−
          colorFlip(h);
 
−
  '''return''' h;
 
−
  }
 
  
−
==Удаление==
+
[[File:34-nodeRemove.png|310px|thumb|center| Узлы до и после удаления]]  
−
f cient implementation of the delete operation is a challenge in many symbol-table implementa- tions, and red-black trees are no exception. Industrial-strength implementations run to over 100 lines of code, and text books generally describe the operation in terms of detailed case studies, eschewing full implementations. Guibas and Sedgewick presented a delete implementation in [7], but it is not fully speci ed and depends on a call-by-reference approach not commonly found in modern code. The most popular method in common use is based on a parent pointers (see [6]), which adds substantial overhead and does not reduce the number of cases to be handled.
+
* Удаление узла с <tex>2</tex>-я потомками нарушает баланс
−
The code on the next page is a full implementation of <tex>delete()</tex> for LLRB 2-3 trees. It is based on the reverse of the approach used for insert in top-down 2-3-4 trees: we perform rotations and color  ips on the way down the search path to ensure that the search does not end on a 2-node, so that we can just delete the node at the bottom. We use the method <tex>fixUp()</tex> to share the code for the color  ip and rotations following the
+
Соответственно, спускаясь вниз по дереву необходимо поддерживать следующий инвариант : количество потомков узла не должно быть ровно <tex>2</tex>-м.
−
recursive calls in the <tex>insert()</tex> code.With <tex>fixUp()</tex>, we can leave right-leaning red links and unbalanced 4-nodes along the search path, secure
+
[[File:changeNode.png|600px|thumb|center| ]]  
−
that these conditions will be  xed on the way up the tree. (The approach is also effective 2-3-4 trees, but requires an extra rotation when the right node
 
−
off the search path is a 4-node.)
 
−
As a warmup, consider the delete-the-minimum operation, where the goal is to delete the bottom node on the left spine while maintaining balance. To do so, we maintain the invariant that the current node or its left child is red. We can do so by moving to the left unless the current node is red and its left child and left grandchild are both black. In that case, we can do a color  ip, which restores the invariant but may introduce successive reds on the right. In that case, we can correct the condition with two rotations and a color  ip. These operations are implemented in the <tex>moveRedLeft()</tex> method on the next page. With <tex>moveRedLeft()</tex>, the recursive implementation of <tex>deleteMin()</tex> above is straightforward.
 
−
For general deletion, we also need <tex>moveRedRight()</tex>, which is similar, but simpler, and we need to rotate left-leaning red links to the right on the search path to maintain the invariant. If the node to be deleted is an internal node, we replace its key and value  elds with those in the minimum node in its right subtree and then delete the minimum in the right subtree (or we could rearrange pointers to use the node instead of copying  elds). The full implementation of <tex>delete()</tex> that dervies from this discussion is given on the facing page. It uses one-third to one-quarter the amount of code found in typical implementations. It has been demonstrated before [2, 11, 13] that maintaining a  eld in each node containing its height can lead to code for delete that is similarly concise, but that extra space is a high price to pay in a practical implementation. With <tex>LLRB</tex> trees, we can arrange for concise code having a logarithmic performance guarantee and using no extra space.
 
 
   
 
   
 +
Будем поддерживать инвариант: для любого узла либо сам узел, либо правый предок узла '''красный'''.
 +
Будем придерживаться тактики , что удалять лист легче, чем внутренний узел.
  
−
'''void''' deleteMin()
+
Заметим, что если правый потомок вершины и правый потомок правого потомка вершины черные, необходимо переместить левую красную ссылку вправо для сохранения инварианта.
−
  root = deleteMin(root);
+
[[File:MinEasy.png|400px|thumb|right| Перемещение красной ссылки. Простой случай]]
−
  root.color = BLACK;
 
  
 +
[[File:MinHard.png|400px|thumb|right| Перемещение красной ссылки. Сложный случай]]
  
−
'''Node''' deleteMin(h : '''Node''')
+
===Псевдокод===
−
  if (h.left == ''null'') '''return''' ''null'';
+
  '''void''' deleteMax()            
−
  '''if !'''isRed(h.left) '''&&  !'''isRed(h.left.left)
+
    root = deleteMax(root)        
−
      h = moveRedLeft(h);
+
    root.color = BLACK             
−
  h.left = deleteMin(h.left);
 
−
'''return''' fixUp(h);
 
  
−
Delete-the-minimum code for LLRB 2-3 trees
+
'''Node''' moveRedLeft(h : '''Node''')
 +
    colorFlip(h)                   
 +
    '''if''' isRed(h.right.left               
 +
        h.right = rotateRight(h.right)     
 +
        h = rotateLeft(h)                 
 +
        colorFlip(h)                         
 +
    '''return''' h                                         
  
−
  '''void''' deleteMin():
+
  '''Node''' deleteMax(h : '''Node''')
−
  root = deleteMin(root)
+
    '''if''' isRed(h.left)                                       
−
  root.color = BLACK
+
    <span style="color:#008000">// вращаем все 3-вершины вправо</span>
 +
        h = rotateRight(h)
 +
    <span style="color:#008000">// поддерживаем инвариант (h должен быть красным)</span>
 +
    '''if''' h.right == ''null''
 +
        return ''null''
 +
    <span style="color:#008000">// заимствуем у брата если необходимо</span>
 +
    '''if''' !isRed(h.right) '''&&''' !isRed(h.right.left)
 +
        h = moveRedRight(h)
 +
    <span style="color:#008000">// опускаемся на один уровень глубже </span>
 +
    h.left = deleteMax(h.left)
 +
    <span style="color:#008000">// исправление правых красных ссылок и 4-вершин на пути вверх</span>
 +
    '''return''' fixUp(h)
  
 +
==Удаление минимума==
 +
Поддерживаем инвариант: вершина или левый ребенок вершины красный.
  
−
  '''Node''' deleteMin( h : '''Node'''):
+
Заметим, что если  левый потомок вершины и левый потомок левого потомка вершины черные, необходимо переместить красную ссылку для сохранения инварианта.
−
  '''if''' h.left == ''null''
+
[[File:MoveRedLeftEasy.png.png |400px|thumb|upright|Перемещение красной ссылки. Простой случай]]
−
      '''return''' ''null''
+
[[File:MoveRedLeftNoEasy.png|400px|thumb|upright|Перемещение красной ссылки. Сложный случай]]
−
  '''if''' !isRed(h.left) '''&&''' !isRed(h.left.left)
+
===Псевдокод===
−
      h = moveRedLeft(h)
+
  '''Node''' moveRedLeft(h : '''Node''')
−
  h.left = deleteMin(h.left)
+
    colorFlip(h)
−
'''return''' fixUp(h)
+
    if isRed(h.right.left)
 +
        h.right = rotateRight(h.right)
 +
        h = rotateLeft(h)
 +
        colorFlip(h)
 +
    '''return''' h
  
 +
'''void''' deleteMin()
 +
    root = deleteMin(root)
 +
    root.color = BLACK
  
 +
'''Node''' deleteMin(h : '''Node''')
 +
    <span style="color:#008000">// удаляем узел на нижнем уровне(h должен быть красным по инварианту)</span>
 +
    if h.left == ''null'' 
 +
        '''return''' ''null''
 +
      <span style="color:#008000">// Если необходимо, пропушим  красную ссылку вниз</span>
 +
    '''if  (!'''isRed(h.left) '''&&  !'''isRed(h.left.left))
 +
          h = moveRedLeft(h)
 +
      <span style="color:#008000">// опускаемся на уровень ниже </span>
 +
    h.left = deleteMin(h.left)
 +
    '''return''' fixUp(h)
  
−
  '''Node''' moveRedLeft('''Node''' : h):
+
==Асимптотика==
−
    colorFlip(h):
+
Асимптотика методов в левосторонних красно-черных деревьях эквивалентна асимптотике [[Красно-черное дерево|базовой реализации красно-черных деревьях]].
−
    '''if''' isRed(h.right.left)
 
−
      h.right = rotateRight(h.right)
 
−
      h = rotateLeft(h)
 
−
      colorFlip(h)
 
−
'''return''' h 
 
−
 
 
−
 
 
−
  '''Node''' moveRedRight(h :'''Node''' ):
 
−
    colorFlip(h)
 
−
    '''if''' isRed(h.left.left))
 
−
      h = rotateRight(h)
 
−
      colorFlip(h)
 
−
'''return''' h 
 
−
 
 
−
 
 
−
'''void''' delete(key : '''Key'''):
 
−
  root = delete(root, key)
 
−
  root.color = BLACK
 
  
−
 
+
== См.также ==
−
  '''Node''' delete('''Node''' : h, '''Key''' : key):
+
*[[Красно-черное дерево]]
−
    '''if''' key.compareTo(h.key) < 0)   
+
*[[Дерево поиска, наивная реализация]]
−
          '''if''' !isRed(h.left) '''&&''' !isRed(h.left.left)
+
==Источники информации==
−
            h = moveRedLeft(h)
+
* Robert Sedgewick "Left-leaning Red-Black Trees" ,Department of Computer Science, Princeton University
−
          h.left =  delete(h.left, key)
+
[[Категория: Алгоритмы и структуры данных]]
−
    '''else''' 
 
−
      '''if''' isRed(h.left)
 
−
        h = rotateRight(h)
 
−
      '''if''' key.compareTo(h.key) == 0 '''&&''' (h.right == null)
 
−
        '''return''' ''null''
 
−
      '''if''' !isRed(h.right) '''&&''' !isRed(h.right.left)
 
−
        h = moveRedRight(h)
 
−
      '''if''' key.compareTo(h.key) == 0
 
−
        h.val = get(h.right, min(h.right).key)
 
−
        h.key = min(h.right).key
 
−
        h.right = deleteMin(h.right)
 
−
      '''else'''
 
−
        h.right = delete(h.right, key)
 
−
  '''return''' fixUp(h)
 

Текущая версия на 19:08, 4 сентября 2022

Определение:
Левостороннее красно-черное дерево — тип сбалансированного двоичного дерева поиска, гарантирующий такую же асимптотическую сложность операций, как у красно-черного дерева поиска.


Свойства

  • Корневой узел всегда черный.
  • Каждый новый узел всегда окрашен в красный цвет.
  • Каждый дочерний нулевой узел листа дерева считается черным.

Вращения

Чтобы поддерживать левосторонние красно-черные двоичные деревья поиска необходимо соблюдать следующие инварианты при вставке и удалении:

  • Ни один путь от корня до листьев дерева не содержит двух последовательных красных узлов.
  • Количество черных узлов на каждом таком пути одинаково.

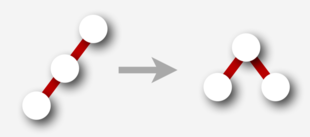
Основные операции, используемые алгоритмами сбалансированного дерева для поддержания баланса при вставке и удалении, называются вращением вправо и вращением влево. Первая операция трансформируют [math]3[/math]-узел (совокупность из [math]3[/math] узлов, где [math]2[/math] узла являются наследниками третьего, причем одна из связей является красной), левый потомок которого окрашен в красный, в [math]3[/math]-узел, правый потомок которого окрашен в красный,вторая операция — наоборот. Вращения сохраняют два указанных выше инварианта, не изменяют поддеревья узла.

Псевдокод

Rotate Right
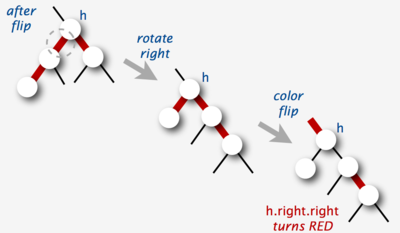
  Node rotateRight(h : Node) 
      x = h.left
      h.left = x.right
      x.right = h
      x.color = h.color
      h.color = RED
      return x
Rotate Left
  Node rotateLeft(h : Node) 
      x = h.right
      h.right = x.left
      x.left = h
      x.color = h.color
      h.color = RED
      return x

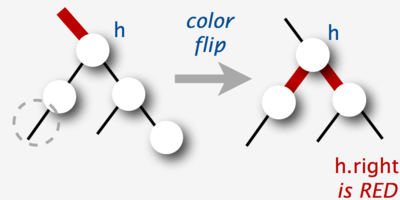
Переворот цветов

В красно-черных деревьях используется такая операция как переворот цветов , которая инвертирует цвет узла и двух его детей. Она не изменяет количество черных узлов на любом пути от корня до листа, но может привести к появлению двух последовательных красных узлов.

Псевдокод

Переворот цветов
 void flipColors(h : Node h) 
      h.color = ! h.color
      h.left.color = ! h.left.color
      h.right.color = ! h.right.color

Вставка

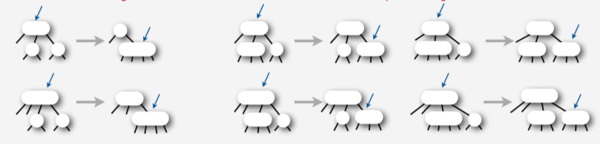
Вставка в ЛСКЧД базируется на [math]4[/math] простых операциях:

  • Вставка нового узла к листу дерева:

Если высота узла нулевая, возвращаем новый красный узел.

Вставка нового узла
  • Расщепление узла с [math]4[/math]-я потомками:

Если левый предок и правый предок красные, запускаем переворот цветов от текущего узла.

Расщепление узла
  • Принудительное вращение влево:
Принудительное вращение

Если правый предок красный, вращаем текущую вершину влево.

  • Балансировка узла с [math]4[/math]-я потомками:
Балансировка

Если левый предок красный и левый предок левого предка красный, то вращаем текущую вершину вправо.


Псевдокод

 void insert(key : Key, value : Value ) 
        root = insert(root, key, value)
        root.color = BLACK



 Node insert(h : Node, key : Key, value : Value)
      // Вставка нового листа
     if h == null     
         return new Node(key, value)
      // Расщепление узла с [math]4[/math]-я потомками
     if isRed(h.left) && isRed(h.right)
         colorFlip(h)
      // Стандартная вставка в дереве поиска
     if key = h.key 
         h.val = value
     else 
         if key < h.key  
             h.left = insert(h.left, key, value)  
         else 
             h.right = insert(h.right, key, value)
          // Принудительное вращение влево
         if isRed(h.right) && !isRed(h.left)
             h = rotateLeft(h)
          // Балансировка узла с [math]4[/math]-я потомками
         if isRed(h.left) && isRed(h.left.left)
             h = rotateRight(h)
     return h

Поиск

Поиск в левосторонних красно-черных деревьях эквивалентен поиску в наивной реализации дерева поиска. Для поиска элемента в красно-черных деревьях дереве поиска можно воспользоваться циклом,который проходит от корня до искомого элемента. Если же элемент отсутствует, цикл пройдет до листа дерева и прервется. Для каждого узла цикл сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае цикл повторяет для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы [math]O(h)[/math], где [math]h[/math] — высота дерева.

Псевдокод

Value search(key : Key)
    Node x = root
    while (x != null)
      if key = x.key
          return x.val
      else
          if key < x.key
              x = x.left
      else 
          if key > x.key 
              x = x.right
    return null

Исправление правых красных связей

  • Использование Переворота цветов и вращений сохраняет баланс черной связи.
  • После удаления необходимо исправить правые красные связи и устранить узлы с [math]4[/math]-я потомками
      // Исправление правых красных связей
  Node fixUp(h : Node)  
      if isRed(h.right)  
          h = rotateLeft(h)  
      // Вращение [math]2[/math]-ой красной пары пары
      if isRed(h.left) && isRed(h.left.left)
          h = rotateRight(h)  
      // Балансировка узла с [math]4[/math]-я потомками
      if isRed(h.left) && isRed(h.right)
          colorFlip(h)  
      return h

Удаление максимума

  • Спускаемся вниз по правому краю дерева.
  • Если поиск заканчивается на узле с [math]4[/math]-мя или [math]5[/math]-ю потомками, просто удаляем узел.
Узлы до и после удаления
  • Удаление узла с [math]2[/math]-я потомками нарушает баланс

Соответственно, спускаясь вниз по дереву необходимо поддерживать следующий инвариант : количество потомков узла не должно быть ровно [math]2[/math]-м.

ChangeNode.png

Будем поддерживать инвариант: для любого узла либо сам узел, либо правый предок узла красный. Будем придерживаться тактики , что удалять лист легче, чем внутренний узел.

Заметим, что если правый потомок вершины и правый потомок правого потомка вершины черные, необходимо переместить левую красную ссылку вправо для сохранения инварианта.

Перемещение красной ссылки. Простой случай
Перемещение красной ссылки. Сложный случай

Псевдокод

void deleteMax()              
    root = deleteMax(root)         
    root.color = BLACK               

Node moveRedLeft(h : Node)
    colorFlip(h)                     
    if isRed(h.right.left                
        h.right = rotateRight(h.right)       
        h = rotateLeft(h)                   
        colorFlip(h)                          
    return h                                           

Node deleteMax(h : Node)
    if isRed(h.left)                                         
    // вращаем все 3-вершины вправо
        h = rotateRight(h)
    // поддерживаем инвариант (h должен быть красным)
    if h.right == null
        return null
    // заимствуем у брата если необходимо
    if !isRed(h.right) && !isRed(h.right.left) 
        h = moveRedRight(h)
    // опускаемся на один уровень глубже 
    h.left = deleteMax(h.left) 
    // исправление правых красных ссылок и 4-вершин на пути вверх
    return fixUp(h)

Удаление минимума

Поддерживаем инвариант: вершина или левый ребенок вершины красный.

Заметим, что если левый потомок вершины и левый потомок левого потомка вершины черные, необходимо переместить красную ссылку для сохранения инварианта.

Перемещение красной ссылки. Простой случай
Перемещение красной ссылки. Сложный случай

Псевдокод

Node moveRedLeft(h : Node)
    colorFlip(h)
    if isRed(h.right.left)
        h.right = rotateRight(h.right)
        h = rotateLeft(h)
        colorFlip(h)
    return h

void deleteMin()
    root = deleteMin(root)
    root.color = BLACK

Node deleteMin(h : Node)
    // удаляем узел на нижнем уровне(h должен быть красным по инварианту)
    if h.left == null   
        return null
     // Если необходимо, пропушим  красную ссылку вниз
    if  (!isRed(h.left) &&  !isRed(h.left.left))
         h = moveRedLeft(h)
     // опускаемся на уровень ниже 
    h.left = deleteMin(h.left)
    return fixUp(h)

Асимптотика

Асимптотика методов в левосторонних красно-черных деревьях эквивалентна асимптотике базовой реализации красно-черных деревьях.

См.также

Источники информации

  • Robert Sedgewick "Left-leaning Red-Black Trees" ,Department of Computer Science, Princeton University
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Левосторонние_красно-чёрные_деревья&oldid=84519»