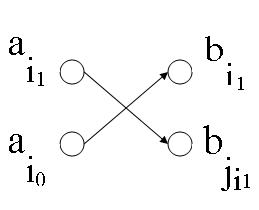Лемма о единственном паросочетании в подграфе замен, индуцированном кратчайшим путем

Лемма:

Пусть дан двудольный граф замен. В его правой доле можно выделить два подмножества вершин [math]X_1 = \{z \in S \setminus I \mid I \cup z \in I_1 \}, X_2 = \{z \in S \setminus I \mid I \cup z \in I_2 \}[/math]. Пусть [math]P[/math] — кратчайший путь из [math]X_1[/math] в [math]X_2[/math]. Рассмотрим сужение [math]G'[/math] графа [math]G[/math] на множество вершин, лежащих в пути [math]P[/math]. Тогда в [math]G'[/math] существует единственное полное паросочетание.

Доказательство:

[math]\triangleright[/math]

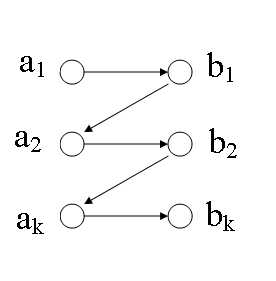
Рис. 1 Рис. 2 Строго говоря, утверждение теоремы не совсем корректно, так как в правой доле полученного графа [math]G'[/math] вершин на одну больше, чем в левой. Поэтому добавим в [math]G'[/math] фиктивную вершину и отнесем ее к левой доле. Пусть путь [math]P = (a_1, b_1, a_2, b_2, \ldots , a_k, b_k)[/math], где [math]a_1[/math] — фиктивная вершина (рис. 1). Существование полного паросочетания очевидно — это ребра [math](a_i,b_i)[/math]. Предположим, что существует другое паросочетание [math](a_i, b_{j_i})[/math]. Тогда пусть [math]i_0 = \min \{ i \: \mid \: j_i \lt i \}[/math]. Обозначим [math]j_{i_0}[/math] как [math]i_1[/math]. Заметим, что [math]i_1 \lt i_0[/math] и поэтому не может быть [math]j_{i_1} \lt i_1[/math], ведь [math]i_0[/math] — минимальное из соответствующего множества. Так же невозможно [math]j_{i_1} = i_1[/math], поскольку тогда [math]a_{i_0}[/math] и [math]a_{i_1}[/math] имели бы одинаковую пару. Следовательно, [math]j_{i_1} \gt i_1[/math] (рис. 2). Это значит, что существует путь [math]P_1 = (a_1, b_1, \ldots, a_{i_1}, b_{j_{i_1}}, a_{j_{i_1} + 1}, \ldots, a_k, b_k )[/math] короче, чем [math]P[/math]. Противоречие.

[math]\triangleleft[/math]