Машина Тьюринга — различия между версиями
Nafanya (обсуждение | вклад) (тикет 3.14) |
Nafanya (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | '''Машина Тьюринга''' (англ. ''Turing machine'') — модель абстрактного вычислителя, предложенная британским математиком Аланом Тьюрингом в 1936 году. Эта модель позволила Тьюрингу доказать два утверждения. Первое | + | '''Машина Тьюринга''' (англ. ''Turing machine'') — модель абстрактного вычислителя, предложенная британским математиком Аланом Тьюрингом в 1936 году. Эта модель позволила Тьюрингу доказать два утверждения. Первое — проблема останова неразрешима, т.е. не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте зациклится или прекратит работу. Второе — не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте когда-нибудь напечатает заданный символ. В этом же году был высказан тезис Чёрча-Тьюринга, который терминах теории рекурсии формулируется как точное описание интуитивного понятия вычислимости классом общерекурсивных функций. В этой формулировке часто упоминается как просто тезис Чёрча. В терминах вычислимости по Тьюрингу тезис гласит, что для любой алгоритмически вычислимой функции существует вычисляющая её значения машина Тьюринга. В виду того, что классы частично вычислимых по Тьюрингу и частично рекурсивных функций совпадают, утверждение объединяют в единый тезис Чёрча — Тьюринга. |
Неформально машина Тьюринга определяется как устройство, состоящее из двух частей: | Неформально машина Тьюринга определяется как устройство, состоящее из двух частей: | ||
| Строка 11: | Строка 11: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | Формально '''машина Тьюринга''' определяется как кортеж из восьми элементов <tex>\langle \Sigma, \Pi, B, Q, Y, N, S, \delta \rangle</tex>, где | + | Формально '''машина Тьюринга''' (англ. ''Turing machine'') определяется как кортеж из восьми элементов <tex>\langle \Sigma, \Pi, B, Q, Y, N, S, \delta \rangle</tex>, где |
| − | * <tex>\Sigma</tex> — алфавит, из букв которого могут состоять входные слова | + | * <tex>\Sigma</tex> — алфавит, из букв которого могут состоять входные слова, |
| − | * <tex>\Pi \supset \Sigma</tex> — символы, которые могут быть записаны на ленту в процессе работы машины | + | * <tex>\Pi \supset \Sigma</tex> — символы, которые могут быть записаны на ленту в процессе работы машины, |
| − | * <tex>B \in \Pi \setminus \Sigma</tex> — пробельный символ (от слова ''blank'') | + | * <tex>B \in \Pi \setminus \Sigma</tex> — пробельный символ (от слова ''blank''), |
| − | * <tex>Q</tex> — множество состояний управляющего автомата | + | * <tex>Q</tex> — множество состояний управляющего автомата, |
| − | * <tex>Y \in Q</tex> — допускающее состояние автомата | + | * <tex>Y \in Q</tex> — допускающее состояние автомата, |
| − | * <tex>N \in Q</tex> — отвергающее состояние автомата | + | * <tex>N \in Q</tex> — отвергающее состояние автомата, |
| − | * <tex>S \in Q</tex> — стартовое состояние автомата | + | * <tex>S \in Q</tex> — стартовое состояние автомата, |
* <tex>\delta : Q \times \Pi \to Q \times \Pi \times \{ \leftarrow, \rightarrow, \downarrow \}</tex> — всюду определённая функция перехода автомата | * <tex>\delta : Q \times \Pi \to Q \times \Pi \times \{ \leftarrow, \rightarrow, \downarrow \}</tex> — всюду определённая функция перехода автомата | ||
}} | }} | ||
| Строка 36: | Строка 36: | ||
|definition= | |definition= | ||
Определим на конфигурациях отношение перехода <tex>\langle w_1, q_1, v_1 \rangle \vdash \langle w_2, q_2, v_2 \rangle</tex>: | Определим на конфигурациях отношение перехода <tex>\langle w_1, q_1, v_1 \rangle \vdash \langle w_2, q_2, v_2 \rangle</tex>: | ||
| − | * если <tex>\delta(q, x) = \langle p, y, \leftarrow \rangle</tex>, то <tex>\langle wz, q, xv \rangle \vdash \langle w, p, zyv \rangle</tex> | + | * если <tex>\delta(q, x) = \langle p, y, \leftarrow \rangle</tex>, то <tex>\langle wz, q, xv \rangle \vdash \langle w, p, zyv \rangle</tex>, |
| − | * если <tex>\delta(q, x) = \langle p, y, \rightarrow \rangle</tex>, то <tex>\langle w, q, xv \rangle \vdash \langle wy, p, v \rangle</tex> | + | * если <tex>\delta(q, x) = \langle p, y, \rightarrow \rangle</tex>, то <tex>\langle w, q, xv \rangle \vdash \langle wy, p, v \rangle</tex>, |
| − | * если <tex>\delta(q, x) = \langle p, y, \downarrow \rangle</tex>, то <tex>\langle w, q, xv \rangle \vdash \langle w, p, yv \rangle</tex> | + | * если <tex>\delta(q, x) = \langle p, y, \downarrow \rangle</tex>, то <tex>\langle w, q, xv \rangle \vdash \langle w, p, yv \rangle</tex>, |
Особо следует рассмотреть случай переходов по пробельному символу: | Особо следует рассмотреть случай переходов по пробельному символу: | ||
| Строка 146: | Строка 146: | ||
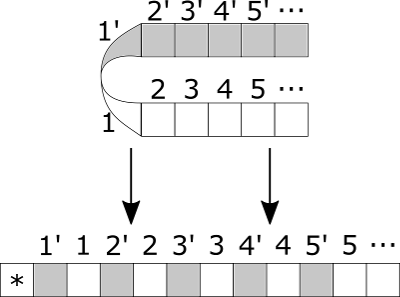
|proof=Существует алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Сначала занумеруем ячейки рабочей ленты машины Тьюринга с ''бесконечной лентой'' следующим образом: | |proof=Существует алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Сначала занумеруем ячейки рабочей ленты машины Тьюринга с ''бесконечной лентой'' следующим образом: | ||
| − | [[Файл:Mt1. | + | [[Файл:Mt1.png]] |
Затем перенумеруем ячейки, и запишем символ <tex>c \in \Pi \setminus \Sigma, B</tex> в начало ленты, который будет означать границу рабочей зоны: | Затем перенумеруем ячейки, и запишем символ <tex>c \in \Pi \setminus \Sigma, B</tex> в начало ленты, который будет означать границу рабочей зоны: | ||
| − | [[Файл:Mt2. | + | [[Файл:Mt2.png]] |
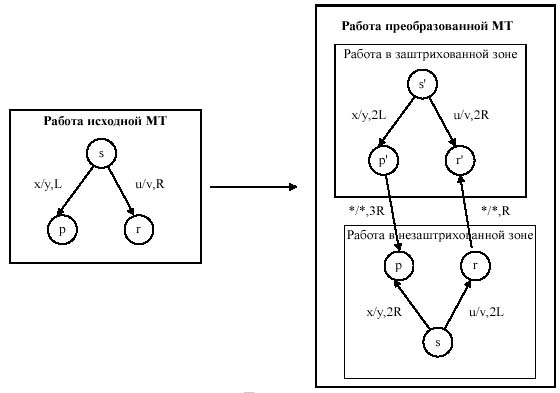
Наконец, изменим машину Тьюринга, удвоив число её состояний, и изменим сдвиг головки так, чтобы в одной группе состояний работа машины была бы эквивалентна её работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе машины Тьюринга встретится символ <tex>c</tex>, значит головка достигла границы рабочей зоны: | Наконец, изменим машину Тьюринга, удвоив число её состояний, и изменим сдвиг головки так, чтобы в одной группе состояний работа машины была бы эквивалентна её работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе машины Тьюринга встретится символ <tex>c</tex>, значит головка достигла границы рабочей зоны: | ||
| Строка 165: | Строка 165: | ||
Каждый шаг исходной машины эмулируется конечной последовательностью шагов построенной машины следующим образом: исходно головка находится в позиции самой левой отметки и идёт вправо до самой правой отметки, запоминая прочитанные около символов <tex>*</tex> символы в состоянии. Пройдя до самой правой отметки, головка возвращается влево, совершая необходимые действия (переписывая символы около отметок и передвигая сами отметки). После такого прохода головка переходит в следующее состояние, завершая эмуляцию шага. | Каждый шаг исходной машины эмулируется конечной последовательностью шагов построенной машины следующим образом: исходно головка находится в позиции самой левой отметки и идёт вправо до самой правой отметки, запоминая прочитанные около символов <tex>*</tex> символы в состоянии. Пройдя до самой правой отметки, головка возвращается влево, совершая необходимые действия (переписывая символы около отметок и передвигая сами отметки). После такого прохода головка переходит в следующее состояние, завершая эмуляцию шага. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Аланом Тьюрингом было сформулировано следующее утверждение: | Аланом Тьюрингом было сформулировано следующее утверждение: | ||
| Строка 185: | Строка 177: | ||
Существует машина Тьюринга, которая принимает на вход закодированное описание произвольной машины и входную строку и эмулирует работу закодированной машины на заданном входном слове. Иными словами, [[Разрешимые (рекурсивные) языки#Пример неразрешимого множества|универсальный язык]] перечислим с помощью машины Тьюринга. Ссылки на явные конструкции универсальных машин Тьюринга приведены ниже. | Существует машина Тьюринга, которая принимает на вход закодированное описание произвольной машины и входную строку и эмулирует работу закодированной машины на заданном входном слове. Иными словами, [[Разрешимые (рекурсивные) языки#Пример неразрешимого множества|универсальный язык]] перечислим с помощью машины Тьюринга. Ссылки на явные конструкции универсальных машин Тьюринга приведены ниже. | ||
| + | |||
| + | == См. также == | ||
| + | * [[Стековые машины, эквивалентность двухстековой машины МТ|стековые машины]] | ||
| + | * [[Счетчиковые машины, эквивалентность двухсчетчиковой машины МТ|счётчиковые машины]] | ||
| + | * [[Линейный клеточный автомат, эквивалентность МТ|клеточные автоматы]] | ||
| + | * [[Возможность порождения формальной грамматикой произвольного перечислимого языка|произвольные формальные грамматики]] | ||
| + | * [[Лямбда-исчисление|нетипизированное лямбда-исчисление]] | ||
== Источники информации == | == Источники информации == | ||
| Строка 194: | Строка 193: | ||
[[Категория: Теория формальных языков]] | [[Категория: Теория формальных языков]] | ||
| + | [[Категория: Теория вычислимости]] | ||
| + | [[Категория: Вычислительные формализмы]] | ||
Версия 17:19, 14 января 2016
Машина Тьюринга (англ. Turing machine) — модель абстрактного вычислителя, предложенная британским математиком Аланом Тьюрингом в 1936 году. Эта модель позволила Тьюрингу доказать два утверждения. Первое — проблема останова неразрешима, т.е. не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте зациклится или прекратит работу. Второе — не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте когда-нибудь напечатает заданный символ. В этом же году был высказан тезис Чёрча-Тьюринга, который терминах теории рекурсии формулируется как точное описание интуитивного понятия вычислимости классом общерекурсивных функций. В этой формулировке часто упоминается как просто тезис Чёрча. В терминах вычислимости по Тьюрингу тезис гласит, что для любой алгоритмически вычислимой функции существует вычисляющая её значения машина Тьюринга. В виду того, что классы частично вычислимых по Тьюрингу и частично рекурсивных функций совпадают, утверждение объединяют в единый тезис Чёрча — Тьюринга.
Неформально машина Тьюринга определяется как устройство, состоящее из двух частей:
- бесконечной одномерной ленты, разделённой на ячейки,
- головки, которая представляет собой детерминированный конечный автомат.
При запуске машины Тьюринга на ленте написано входное слово, причём на первом символе этого слова находится головка, а слева и справа от него записаны пустые символы. Каждый шаг головка может перезаписать символ под лентой и сместиться на одну ячейку, если автомат приходит в допускающее или отвергающее состояние, то работа машины Тьюринга завершается.
Содержание
Определение
Определение машины
| Определение: |
Формально машина Тьюринга (англ. Turing machine) определяется как кортеж из восьми элементов , где
|
Отметим, что существуют различные вариации данного выше определения (например, без отвергающего состояния или с множеством допускающих состояний), которые не влияют на вычислительные способности машины Тьюринга.
Определение процесса работы
Кроме формального определения самой машины требуется также формально описать процесс её работы. В определении для простоты будем предполагать, что головка в процессе работы не записывает на ленту символ . Это не ограничивает вычислительной мощности машин Тьюринга, поскольку для каждой машины можно сопоставить аналогичную ей, но не пищущую на ленту.
| Определение: |
| Назовём конфигурацией машины Тьюринга тройку , где — текущее состояние автомата, а — строки слева и справа от головки до первого пробельного символа соответственно. |
В данной записи головка находится над ячейкой, на которой написана первая буква (или , если ).
В дальнейшем используются следующие обозначения: ,
| Определение: |
Определим на конфигурациях отношение перехода :
Особо следует рассмотреть случай переходов по пробельному символу:
|
Очевидно, что определённое отношение является функциональным: для каждой конфигурации существует не более одной конфигурации , для которой .
Для машины Тьюринга, которая пишет символ на ленту также можно дать аналогичное формальное определение. Оно будет отличаться тем, что символы в строчках конфигурации могут содержать пробелы, и для того, чтобы эти строчки имекли конечную длину, нужно аккуратно учесть наличие пробелов при записи правил перехода.
Результат работы
Машину Тьюринга можно рассматривать как распознаватель слов формального языка. Пусть — машина Тьюринга, распознаваемый ей язык определяется как .
Также можно рассматривать машины Тьюринга как преобразователь входных данных в выходные. Машина задаёт вычислимую функцию , причём . Переход автомата в состояние можно интерпретировать как аварийное завершение программы (например, при некорретном входе).
Примеры машин-распознавателей и машин-преобразователей будут даны ниже.
Примеры машин Тьюринга
Прибавление единицы
Для начала приведём пример машины-преобразователя, которая прибавляет единицу к числу, записанному на ленте в двоичной записи от младшего бита к старшему. Алгоритм следующий:
- в стартовом состоянии головка идёт вправо от младшего бита к старшему, заменяя все единицы на нули,
- встретив нуль или пробельный символ головка записывает единицу, после чего переходит в состояние ,
- в состоянии головка идёт влево от старшего бита к младшему, не изменяя символы 0 и 1 на ленте,
- встретив в состоянии пробельный символ, головка перемещается на один символ вправо и переходит в состояние , завершая работу.
Формально: , , . Таблица функции приведена ниже:
Проверка того, является ли слово палиндромом
В качестве примера машины-распознавателя приведём машину, распознающую палиндромы над алфавитом . Алгоритм следующий:
- если строка на ленте — пустая, то перейти в допускающее состояние
- надо запомнить первый символ слова в состоянии автомата,
- стереть его,
- перейти в конец ленты:
- если оставшаяся строка на ленте — пустая, то перейти в допускающее состояние
- если последний символ совпадает с запомненным, стереть его, перейти в начало ленты и повторить с первого шага
- в случае несовпадения перейти в отвергающее состояние
Формально: , , . Таблица функции приведена ниже:
Варианты машины Тьюринга
В этом разделе приведены различные варианты машин Тьюринга, которые не отличаются от обычных машин Тьюринга по вычислительной мощности.
Многодорожечная машина Тьюринга
Машиной Тьюринга с дорожками называется вычислитель, аналогичный машине Тьюринга, лишь с тем отличием, что лента состоит из дорожек, на каждой из которых записаны символы ленточного алфавита. У многодорожечной машины одна головка, которая за один шаг переходит в одном направлении на всех дорожках одновременно. Соответственно, функция перехода имеет тип . Многодорожечная машина Тьюринга тривиально эквивалентна обычной с ленточным алфавитом .
Машина Тьюринга с полубесконечной лентой
Заменив у машины Тьюринга бесконечную в обе стороны ленту на бесконечную в одну сторону, мы не теряем в вычислительной мощности. По произвольной машине Тьюринга строится двухдорожечная машина с полубесконечной лентой.
| Теорема: |
Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте. |
| Доказательство: |
|
Существует алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Сначала занумеруем ячейки рабочей ленты машины Тьюринга с бесконечной лентой следующим образом: Затем перенумеруем ячейки, и запишем символ в начало ленты, который будет означать границу рабочей зоны: Наконец, изменим машину Тьюринга, удвоив число её состояний, и изменим сдвиг головки так, чтобы в одной группе состояний работа машины была бы эквивалентна её работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе машины Тьюринга встретится символ , значит головка достигла границы рабочей зоны: Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации. |
Многоленточная машина Тьюринга
В отличие от многодорожечной машины Тьюринга, ленты не зависят друг от друга и головки во время одного шага могу перемещаться по-разному. То есть, функция перехода теперь имеет тип .
Многоленточная машина с дорожками эмулируется многодорожечной машиной с дорожками следующим образом: каждая нечётная дорожка соответствует ленте исходной машины, а на каждой чётной дорожке отмечены специальным символом позиция головки на ленте выше (считаем, что ленты нумеруются сверху вниз).
Каждый шаг исходной машины эмулируется конечной последовательностью шагов построенной машины следующим образом: исходно головка находится в позиции самой левой отметки и идёт вправо до самой правой отметки, запоминая прочитанные около символов символы в состоянии. Пройдя до самой правой отметки, головка возвращается влево, совершая необходимые действия (переписывая символы около отметок и передвигая сами отметки). После такого прохода головка переходит в следующее состояние, завершая эмуляцию шага.
Аланом Тьюрингом было сформулировано следующее утверждение:
| Утверждение (Тезис Чёрча-Тьюринга): |
Класс перечислимых языков совпадает с классом языков, перечислимых с помощью машин Тьюринга |
Иными словами, тезис говорит о том, что любой алгоритм можно запрограммировать на машине Тьюринга.
Универсальная машина Тьюринга
Существует машина Тьюринга, которая принимает на вход закодированное описание произвольной машины и входную строку и эмулирует работу закодированной машины на заданном входном слове. Иными словами, универсальный язык перечислим с помощью машины Тьюринга. Ссылки на явные конструкции универсальных машин Тьюринга приведены ниже.
См. также
- стековые машины
- счётчиковые машины
- клеточные автоматы
- произвольные формальные грамматики
- нетипизированное лямбда-исчисление
Источники информации
- Alan Turing — On computable numbers, with an application to the Entscheidungsproblem.
- F. C. Hennie, R. E. Stearn — Two-tape simulation of multitape Turing machines.
- Sanjeev Arora, Boaz Barak — Computational Complexity: A Modern Approach.
- Turlough Neary, Damien Woods — Four Small Universal Turing Machines.
- JFLAP — ПО для изучения формальных языков, включает в себя эмулятор одноленточных и многоленточных машин Тьюринга с визуальным редактором.