Минимальная охватывающая окружность множества точек
| Конспект готов к прочтению. |
Описание
Минимальная охватывающая окружность множества точек (smallest enclosing disc) - это задача, в которой необходимо по заданному набору точек найти окружность минимального радиуса, которая содержит все точки множества.
Алгоритм
Сперва приведем алгоритм, корректность которого позднее будет доказана.
Рассмотрим метод , который будет принимать на вход множество точек, а возвращать будет искомую охватывающую окружность. Идея метода в том, что он генерирует случайную перестановку из точек, которые поступили на вход и в получившимся порядке по одной добавляет их в текущую охватывающую окружность. Как будет доказано позднее, если на каком-то шаге алгоритма текущая точка оказалась вне текущей минимальной окружности, то утверждается, что она лежит на границе новой окружности, которая будет содержать в себе ее и все предыдущие точки. Опишем приведенный выше алгоритм псевдокодом:
MinDisc(S)
Let P - random permutation of S
Let D2 - be the smallest enclosing disc for {p1, p2}.
for i = 3 to n {
if pi Di−1 then Di = Di−1 // point is inside. nothing to do here
else Di = MinDiscWithPoint ({p1,...,pi−1}, pi) // point is lying on the boundary of minimal circle
}
return Dn
Как вы заметили, мы использовали выше метод - это метод, который по множеству точек и еще одной точке возвращают искомую окружность. При этом выделенная точка (которая передается в качестве второго аргумента) обязательно лежит на окружности. Эта функция очень похожа на предыдущую, поэтому приведу лишь ее псевдокод:
MinDiscWithPoint(S, q)
Let P - random permutation of S
Let D1 - be the smallest enclosing disc for {p1, q}.
for i = 2 to n {
if pi Di−1 then Di = Di−1
else Di = MinDiscWith2Points ({p1,...,pi−1}, pi, q)
}
return Dn
Как и в предыдущем случае мы использовали новый метод. аналогичен , но в нем уже передается две точки, которые будут лежать на построенной окружности. В этой функции шафлить инпут не требуется. Опишем его псевдоком:
MinDiscWith2Points(P, q1, q2)
Let D0 - be the smallest enclosing disc for {q1, q2}.
for i = 1 to n {
if pi Di−1 then Di = Di−1
else Di = сircumcircle (прим. описанная окружность) of a triangle {pi, q1, q2}
}
return Dn
Как мы видим больше подобных шагов делать не нужно, так как если известно, что три точки лежат на некоторой окружности, то они однозначно ее задают.
Корректность алгоритма
Попробуем разобраться почему этот алгоритм действительно находит искомую окружность.
Докажем несколько вспомогательных лемм. Для удобства введем общие обозначения. Пусть и - два непересекающихся множества точек на плоскоти, Пусть - некоторая точка из множества .
| Лемма (лемма 1): |
Окружность минимального радиуса, содержащая все точки внутри себя и все точки на границе, уникальна. |
| Доказательство: |
|
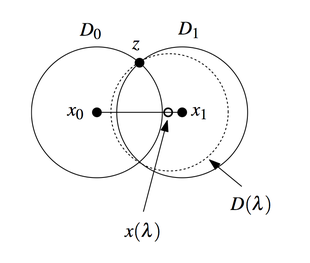
Пусть это не так и существует две такие окружности и . Очевидно, что в таком случае все точки из должны лежать внутри . Пусть - точка пересечения окружностей (смотри рисунок). Рассмотрим некоторое семейство окружностей . При этом центры этих окружностей лежат на отрезке, соединяющем центры и , и перемещаются очевидным образом в зависимости от параметра . При этом радиус каждой из этих окружностей - расстояние от центра до точки , описанной выше. Рассмотрим окружность . Заметим, что лежит целиком внутри нее (по построению окружности ), а так как проходит через пересечение окружностей и , то она проходит через все точки (так все точки лежат на .). Из этого следует, что эта окружность явлется допустимой для нашей теоремы и при этом обладает меньшим радиусом, то наше предположение неверно и искомая окружность единственная.
|
| Лемма (лемма 2): |
Если , то |
| Доказательство: |
| Для множества справедливо, что для него минимальный диск по определению - это , но так как лежит внутри него, то он и является корректным диском для множества . Но если бы в существовал еще меньший диск, то он бы существовал бы и для . Значит эти диски равны(в силу единственности) и |
| Лемма (лемма 3): |
Если , то |
| Доказательство: |
| Пусть и . Рассмотрим аналогичное семейство множеств как в лемме 1. Зададим это семейство с помощью окружностей и . Заметим, что , но . Значит найдется такое , что точка лежит на границе окружности . Но в таком случае так как эта окружность удовлетворяет условиям теоремы и к тому же обладает не большим радиусом, чем (которая в свою очередь является минимальной охватыающей окружностью), то . Это означает, что , то точка лежит на границе , то . |
Эти три доказанные леммы полностью подтверждают корректность наших действий в приведенном выше алгоритме, ведь во всех трех методах в условном операторе мы используем леммы 2 и 3, корректность которых доказана. Другими словами, алгоритм действительно найдет искомую минимальную охватывающую окружность множества точек.
Память и время работы
Сначала разберемся с памятью. Тут все просто - никаких лишних затрат, кроме как на хранение точек нам требуется, то алгоритм требует памяти.
С временем работы дела обстоят интереснее. На самом деле приведенный алгоритм работает за линейное время. Докажем этот факт.
Рассмотрим некоторое множество и точку , которая лежит на границе построенной охватывающей окружности. Тогда попробуем удалить одну точку из набора . Искомая окружность может измениться только в том случае, когда эта удаленная точка лежала на границе, а вероятность этого (так как точек, которые образуют нашу окружность не более трех. при этом одна из этих трех точек - ).
То оценим время работы MinDiscWithPoint c помощью доказанного выше факта. На каждой итерации цикла будет происходить проверка, которая пройдет в "else" с вероятностью . А сложность работы каждого "else" - . То суммарное время работы MinDiscWithPoint вычисляется следующим образом:
.
Абсолютно аналогичным образом доказываем, что время работы есть . То есть рассматриваемый алгоритм имеет линейную сложность.
Источники
Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars-Computational Geometry Algorithms and Applications, p. 86