Минимизация ДКА, алгоритм за O(n^2) с построением пар различимых состояний

Определения

Определение:

Состояния [math]u[/math] и [math]v[/math] различимы строкой [math]s[/math], если [math] \langle u, s \rangle \vdash^* \langle t, \varepsilon \rangle [/math], где [math]t \in T [/math], [math] \langle v, s \rangle \vdash^* \langle z, \varepsilon \rangle [/math], где [math]z \notin T [/math].

Определение:

Состояния [math]u[/math] и [math]v[/math] эквивалентны, если они не различимы никакой строкой.

Теорема:

Если [math]u[/math] и [math]v[/math], [math]v[/math] и [math]z[/math] эквивалентны, то [math]u[/math] и [math]z[/math] эквивалентны.

Доказательство:

[math]\triangleright[/math]

Пусть [math]u[/math] и [math]z[/math] неэквивалентны. Тогда [math] \mathcal {9} s[/math] такая, что [math] \langle u, s \rangle \vdash^* \langle t, \varepsilon \rangle [/math], где [math]t \in T [/math], [math] \langle z, s \rangle \vdash^* \langle t_1, \varepsilon \rangle [/math], где [math]t_1 \notin T [/math]. Рассмотрим [math]x[/math] такой, что [math] \langle v, s \rangle \vdash^* \langle x, \varepsilon \rangle [/math]. Если [math]x \in T[/math], то [math]v[/math] и [math]z[/math] различимы строкой [math]s[/math]. Противоречие. Если [math]x \notin T[/math], то [math]u[/math] и [math]v[/math] различимы строкой [math]s[/math]. Противоречие. Значит, [math]u[/math] и [math]z[/math] эквивалентны.

[math]\triangleleft[/math]

Алгоритм

Основная идея алгоритма заключается в том, чтобы разбить состояния на классы эквивалентности — они и будут состояниями минимизированного автомата.
Для реализации алгоритма нам потребуются очередь [math]Q[/math] и таблица размером [math]n \times n[/math], где [math]n[/math] — количество состояний автомата.
Будем помечать в таблице пары неэквивалентных состояний и класть их в очередь.
Изначально добавим в очередь [math]Q[/math] пары состояний различимых строкой [math] \varepsilon [/math] и пометим их в таблице. Пока [math]Q[/math] не станет пуста, будем делать следующее:

1. Извлечем пару [math] \langle u, v \rangle [/math] из [math]Q[/math].
2. Отметим в таблице и добавим в очередь [math]Q[/math] все пары [math] \langle t, k \rangle [/math] такие, что [math] \mathcal {9} c \in \Sigma, \langle t, c \rangle \vdash \langle u, \varepsilon \rangle, \langle k, c \rangle \vdash \langle v, \varepsilon \rangle [/math], и пара [math] \langle t, k \rangle[/math] не отмечена в таблице.

В момент опустошения очереди пары состояний, не помеченные в таблице, являются парами эквивалентных состояний. За один проход по таблице, согласно теореме, разбиваем пары эквивалентных состояний на классы эквивалентности.
Стартовым состоянием полученного автомата будет состояние, соответствующее классу эквивалентности, содержащему стартовое состояние исходного автомата.
Терминальными состояниями полученного автомата будут состояния, соответствующие классам эквивалентности, содержащим терминальные состояния исходного автомата.

Корректность алгоритма

Пусть в результате применения данного алгоритма к автомату [math]A[/math] мы получили автомат [math]A_{min}[/math]. Докажем, что этот автомат минимальный и единственный с точностью до изоморфизма.
Пусть существует автомат [math]A'[/math] эквивалентный [math]A[/math], но с числом состояний меньшим, чем в [math]A_{min}[/math]. Стартовые состояния [math]s \in A_{min}[/math] и [math]s' \in A'[/math] эквивалентны, так как [math]A_{min}[/math] и [math]A'[/math] допускают один и тот же язык. Рассмотрим строку [math]\alpha = a_1a_2...a_{k}[/math], где [math]a_{i} \in \Sigma[/math] такую, что [math] \langle s, \alpha \rangle \vdash^* \langle u, \varepsilon \rangle [/math], [math] \langle s', \alpha \rangle \vdash^* \langle u', \varepsilon \rangle [/math]. Пусть [math]\langle s, a_1 \rangle \vdash^* \langle l, \varepsilon \rangle [/math] и [math]\langle s', a_1 \rangle \vdash^* \langle l', \varepsilon \rangle [/math]. Так как [math]s[/math] и [math]s'[/math] эквивалентны, то [math]l[/math] и [math]l'[/math] эквивалентны. Аналогично для всех [math]a_{i}[/math]. В итоге получим, что [math]u[/math] эквивалентно [math]u'[/math]. Значит, для каждого состояния из [math]A_{min}[/math] существует эквивалентное состояние из [math]A'[/math].
Состояний в [math]A'[/math] меньше, чем в [math]A_{min}[/math], значит двум состояниям из [math]A_{min}[/math] эквивалентно одно состояние из [math]A'[/math]. Тогда эти два состояния эквивалентны, но автомат [math]A_{min}[/math] построен так, что в нем нет эквивалентных состояний. Противоречие.
Так как каждому состоянию из [math]A_{min}[/math] эквивалентно состояние из [math]A'[/math], то автоматы [math]A_{min}[/math] и [math]A'[/math] изоморфны.

Время работы алгоритма

Каждую пару мы добавляли в очередь один раз, значит время заполнения таблицы [math]O(n^2)[/math]. Разбиение на классы эквивалентности делается за один проход по таблице, то есть за [math]O(n^2)[/math].

Пример

Минимизируем данный автомат.

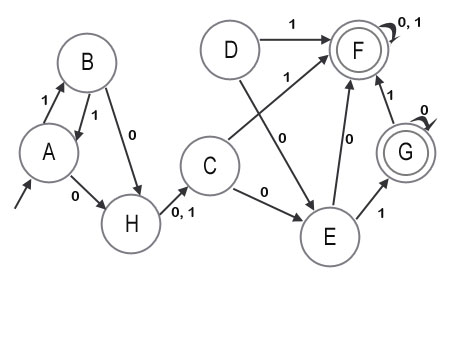
Будем рассматривать только нижний треугольник таблицы пар различимых состояний.
Отметили состояния, различающиеся строкой [math]\varepsilon[/math]:

B
C
D
E
F	x	x	x	x	x
G	x	x	x	x	x
H						x	x
	A	B	C	D	E	F	G

На момент опустошения очереди:

B
C	x	x
D	x	x
E	x	x	x	x
F	x	x	x	x	x
G	x	x	x	x	x
H	x	x	x	x	x	x	x
	A	B	C	D	E	F	G

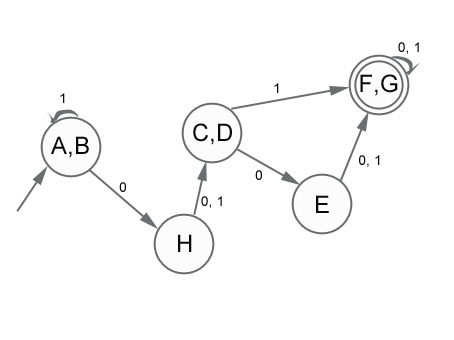
Из таблицы видно, что классы эквивалентных состояний это [math] \mathcal {f} A, B \mathcal {g}, \mathcal {f} C, D \mathcal {g}, \mathcal {f} F, G \mathcal {g}, \mathcal {f} E \mathcal {g}, \mathcal {f} H \mathcal {g} [/math].
Итого получили такой автомат:

Источники

Хопкрофт Д., Мотвани Р., Ульман Д. Введение в теорию автоматов, языков и вычислений, 2-е издание. Пер. с англ. — М.: Издательский дом «Вильямс», 2002. — С. 171 - 182. — ISBN 5-8459-0261-4