Монотонный код Грея — различия между версиями
Shersh (обсуждение | вклад) м (→Псевдокод) |
м |
||
| Строка 77: | Строка 77: | ||
<code>'''yield'''</code> {{---}} аналог <code>'''return'''</code> только для функций-генераторов. То есть генераторы это тоже итерируемые объекты, но прочитать их можно лишь один раз. Это связано с тем, что они не хранят значения в памяти, а генерируют их на лету. | <code>'''yield'''</code> {{---}} аналог <code>'''return'''</code> только для функций-генераторов. То есть генераторы это тоже итерируемые объекты, но прочитать их можно лишь один раз. Это связано с тем, что они не хранят значения в памяти, а генерируют их на лету. | ||
| − | С конструкциями типа <code>(0,)</code> или <code>(1,)</code> все проще. Используя ее совместно с <code>'''yield'''</code> мы можем | + | С конструкциями типа <code>(0,)</code> или <code>(1,)</code> все проще. Используя ее совместно с <code>'''yield'''</code> мы можем изменять наш генерируемый объект. Например, <code>'''yield''' (0,)</code> допишет к генерируемому объекту (в нашем случае кортежу (англ. ''tuple'')) <tex>0</tex> в начало. |
{| border="0" | {| border="0" | ||
|align="left" colspan="4"| | |align="left" colspan="4"| | ||
Версия 13:32, 24 июня 2019
| Определение: |
| Монотонный код Грея (англ. Monotonic Gray Code) — способ построения кода Грея, при котором , что содержит на или больше единиц, чем . |
Монотонный код Грея преимущественно используется в теории связанных сетей, например для минимизации ожидания линейным массивом процессоров.[1]
Содержание
Алгоритм построения
Для начала определим такое понятие, как вес двоичного кода, им будет являтся количество в данном двоичном коде. Очевидно, что нельзя построить код Грея в котором бы вес всегда возрастал. Неплохим решением этой проблемы будет обход всех кодов со смежными с данным весами.
Мы можем формализовать модель монотонных кодов Грея рассматривая разбиение гиперкуба , вершины в котором являются двоичными кодами, на уровни с одинаковым весом вершин.
для . Для всех уровней выполняется соотношение .
Пусть подграф , который является объединением двух смежных уровней, т. е. , и пусть множество граней . Тогда монотонным кодом Грея будет являтся Гамильтонов путь в , при котором любое множество вершин такие, что , то идет перед .
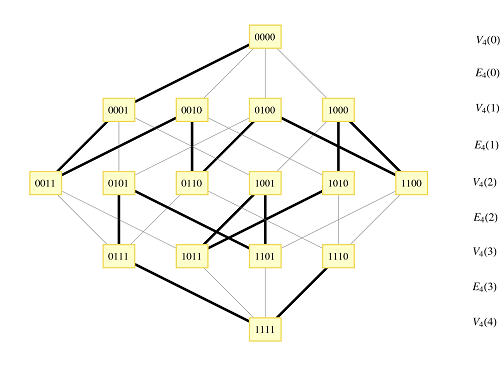
Ниже на катринке Гамильтонов путь в гиперкубе для , построенный по алгоритму Саважа-Винклера (англ. Savage-Winkler).[2]
Элегантная идея построения -ичного монотонного кода Грея состоит в том, чтобы рекурсивно строить подпути длинны включающих вершины .
Определим и , когда или и . То есть это объединение множеств с приписанной в начале и с приписанным в начале .
Здесь это определенная перестановка элементов множества к которому она применена, а это путь к котрому была применена пересатновка . Существует два варианта построить монотонный код грея по путям .
Назовем их и . Будем строить их таким образом:
Выбор перестановки обусловлен тем, чтобы получившиеся коды соответсвовали требованиям кода Грея и поэтому эта перестановка равна .
Чтобы лучше разобратся в том, как сторится этот код и работает перестановка следует рассмотреть таблицу ниже.
Монотонный код Грея может быть эффективно сгенерирован по этому алгоритму за время . Легче всего написать этот алгоритм используя генератор.
Псевдокод
Перед тем как писать псевдокод необходимо объяснить что такое yield и что понимать под выражениями типа (0,) или (1,).
yield — аналог return только для функций-генераторов. То есть генераторы это тоже итерируемые объекты, но прочитать их можно лишь один раз. Это связано с тем, что они не хранят значения в памяти, а генерируют их на лету.
С конструкциями типа (0,) или (1,) все проще. Используя ее совместно с yield мы можем изменять наш генерируемый объект. Например, yield (0,) допишет к генерируемому объекту (в нашем случае кортежу (англ. tuple)) в начало.
|
Вспомогательная функция для генерации перестановки, циклически сдвигает битовый вектор направо раз.
Принимает и возвращает кортеж. Кортеж аналог списка, но в кортеже нельзя менять элементы, можно только добавлять.
function rotateRight(x: int[n]): int[n] return x[-n:] + x[:-n]
Рекурсивная генерация -ой перестановки.
Возвращает перестановку в виде кортежа.
Если становится меньше дописывает в начало кортежа и возвращает его.
function pi(int n): int[n]
if n <= 1
return (0,)
x = pi(n - 1) + (n - 1,)
return rotateRight(tuple(x[k] for k in x), 1)
Рекурсивная генерация пути .
Принимает , а так же дополнительный параметр определяющий надо-ли переворачивать кортеж.
function p(int n, int j, bool reverse = false): list<int[n]>
if n == 1 and j == 0
if not reverse
yield (0,)
yield (1,)
else
yield (1,)
yield (0,)
else if j >= 0 and j < n
perm = pi(n - 1)
if not reverse
for x in p(n - 1, j - 1)
yield (1,) + tuple(x[k] for k in perm)
for x in p(n - 1, j)
yield (0,) + x
else
for x in p(n - 1, j, reverse=true)
yield (0,) + x
for x in p(n - 1, j - 1, reverse=true)
yield (1,) + tuple(x[k] for k in perm)
Генерация монотонного кода Грея при помощи уже написанного генератора .
function monotonic(int n): list<int[n]>
for i in range(n)
for x in (p(n, i) if i % 2 == 0 else p(n, i, reverse=true))
yield x
|
Визуализация работы алгоритма
Для
Для