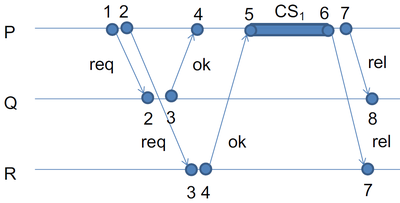
Алгоритм Лампорта взаимного исключения

Алгоритм Лампорта -- алгоритм взаимного исключения, работающий в случае, если все сообщения идут FIFO и использующий логические часы Лампорта (т.е. с каждым сообщением посылается ещё и временна́я метка).

Каждый поток поддерживает очередь запросов на вход в критическую секцию. Приоритет – <временная метка, номер потока> (т.е при равенстве временных меток берем тот поток, чей номер меньше, иначе возможна взаимная блокировка, если процессы будут общаться идеально симметрично).

Когда поток хочет войти в критическую секцию, он:

1. Добавляет свой запрос в свою очередь (т.е временную метку и номер потока)
2. Посылает всем потокам запрос (req)
3. Ждет от них ответа (ok)
4. Получив все ответы, ждет, когда он станет первым в своей очереди, и входит в критическую секцию
5. Выйдя из критической секции, удаляет свой запрос из своей очереди, посылает всем сообщение о том, что вышел (rel)

Действия вне критической секции:

• При получении запроса от другого потока, запрос добавляется в очередь и запрашивающему потоку посылается ответ
• При получении release от другого потока, его запрос удаляется из очереди

Суммарно на каждую критическую секцию приходится [math]3(N - 1)[/math] сообщение.

Корректность гарантируется при помощи FIFO и ok: если $P$ получил ok от процесса $Q$, то запрос от $Q$ на вход в критическую секцию уже тоже получен.

Также гарантируется отсутствие блокировок: если стабилизировалось множество процессов, желающих получить блокировку, то рано или поздно все сообщения доедут, а тогда у всех станут одинаковые очереди (тут стоит аккуратно говорить, почему), и тогда кто-нибудь обязательно станет в очереди первым.

Отсутствие голоданий тоже гарантируется: если процесс хочет получить блокировку, то он рассылает всем сообщения. Процессы, которые захотят блокировку после получения такого сообщения, получат больший номер. То есть нам максимум придётся ждать блокировок, которые возникли до того, как каждый процесс получил наше сообщение.

Доказательство

Неаккуратное

Если $P$ и $Q$ решили одновременно войти в критическую секцию, то они оба получили друг от друга ok и, следовательно, знают друг про друга. А тогда $P$ не может быть минимальным в очереди $P$, а $Q$ — минимальным в очереди $Q$. Почему неаккуратно:

1. Используется запретное слово "одновременно", а не "произошло-до".
2. Нигде нет отсылок к тому, что мы используем логические часы в качестве меток, а не просто случайные числа.

Аккуратное

Не требуется на экзамене, но есть в книжке Gaarg, страницы 24 и 26 (впрочем, там тоже есть "одновременно", но уже не так явно).

Пусть процесс $P_i$ в момент времени $e'$ выбрал для захода в критическую секцию метку $x_i$ ($C(e')=x_i$) и зашёл в неё в момент времени $e$, а процесс $P_k$ в момент времени $f'$ выбрал метку $x_k$ ($C(f)=x_k$). Раз $P_i$ зашёл в секцию, то он, в частности, получил подтверждение от $P_k$. Процесс $P_k$ отправил его в момент $g$ (сразу после получения запроса на подтверждение). Два случая:

1. Если $g < f$ (т.е. $P_k$ решил входить в секцию после того, как узнал про $P_i$), то $x_i = C(e') < C(g) < C(f) = x_k$. То есть процесс $P_k$ знает про $P_i$ и имеет строго больший номер. Тогда он может зайти в критическую секцию только после выхода $P_i$ из секции и получения об этом сообщения, то есть его вход происходит-после выхода $P_i$.
2. Если $f < g$, то процесс $P_i$ получит от $P_k$ сообщение req до того, как получит подтверждение в момент $g$. Таким образом, оба потока знают друг про друга. И раз $P_i$ решил входить в секцию, то либо он уже знает, что $P_k$ вошёл в секцию (при помощи сообщений), либо у него номер строго меньше (тогда $P_k$ не будет входить в секцию, пока $P_i$ не выйдет).

А если без FIFO?

Возможна проблема: процессы одновременно хотят войти в критическую секцию, но сообщение req от первого прилетает второму в тот момент, когда тут уже в критической секции (при этом первый успешно отправил ok второму в ответ на его rel). Тогда второй ответит ok и первый тоже войдёт в критическую секцию как процесс с бОльшим приоритетом. А вот если запретить отвечать ok в критической секции, то вроде как снова будет корректный алгоритм, похожий на алгоритм Рикарта-Агравалы.