Пересечение матроидов, определение, примеры — различия между версиями
м |
м (rollbackEdits.php mass rollback) |
||
| (не показана 21 промежуточная версия 7 участников) | |||
| Строка 5: | Строка 5: | ||
'''Пересечением матроидов''' (англ. ''matroid intersection'') <tex>M_1</tex> и <tex>M_2</tex> называется пара <tex>M_1 \cap M_2 = \langle X, \mathcal{I} \rangle</tex>, где <tex>X</tex> {{---}} носитель исходных матроидов, а <tex> \mathcal{I} = \mathcal{I}_1 \cap \mathcal{I}_2</tex>. | '''Пересечением матроидов''' (англ. ''matroid intersection'') <tex>M_1</tex> и <tex>M_2</tex> называется пара <tex>M_1 \cap M_2 = \langle X, \mathcal{I} \rangle</tex>, где <tex>X</tex> {{---}} носитель исходных матроидов, а <tex> \mathcal{I} = \mathcal{I}_1 \cap \mathcal{I}_2</tex>. | ||
| − | + | }} | |
| − | + | * Пересечение матроидов не всегда является матроидом. | |
| + | * Пересечение трех и более матроидов является [[Примеры NP-полных языков| NP-полной задачей]]. | ||
| − | |||
| − | == | + | == Разноцветный лес == |
| − | <tex>M_1</tex> {{---}} графовый матроид, <tex>M_2</tex> {{---}} '''разноцветный матроид''' (англ. ''multicolored matroid'') (Множество независимо, если в нём нет двух ребер одного цвета). Тогда их пересечение {{---}} это разноцветный лес (англ. ''rainbow forests''). | + | <tex>M_1</tex> {{---}} [[Примеры_матроидов|графовый матроид]], <tex>M_2</tex> {{---}} '''разноцветный матроид''' (англ. ''multicolored matroid'') (Множество независимо, если в нём нет двух ребер одного цвета). Тогда их пересечение {{---}} это '''разноцветный лес''' (англ. ''rainbow forests''). |
| + | [[Файл:Rainbow_forest_DY.png|500px|thumb|center|Пересечение матроидов, [[Алгоритм_построения_базы_в_пересечении_матроидов|база]] матроида]] | ||
{{Утверждение | {{Утверждение | ||
| Строка 19: | Строка 20: | ||
|proof = | |proof = | ||
Рассмотрим пару <tex>\langle X, \mathcal{I}\rangle</tex>, <tex>X</tex> {{---}} ребра разноцветного леса, <tex> \mathcal{I} = \mathcal{I}_1 \cap \mathcal{I}_2</tex>. | Рассмотрим пару <tex>\langle X, \mathcal{I}\rangle</tex>, <tex>X</tex> {{---}} ребра разноцветного леса, <tex> \mathcal{I} = \mathcal{I}_1 \cap \mathcal{I}_2</tex>. | ||
| − | Данная пара не является матроидом, так как не выполняется третье свойство матроида, то есть <tex>\exists A, B \in I, |A| > |B| </tex> и <tex>\nexists \, x \in A \setminus B : B \cup \{x\} \in I</tex> (См. пример 1) | + | Данная пара не является матроидом, так как не выполняется третье свойство матроида, то есть <tex>\exists A, B \in \mathcal{I}, |A| > |B| </tex> и <tex>\nexists \, x \in A \setminus B : B \cup \{x\} \in \mathcal{I}</tex> (См. пример <tex>1</tex>) |
[[Файл:Example2_DY.png|300px|thumb|left|Пример 1]] | [[Файл:Example2_DY.png|300px|thumb|left|Пример 1]] | ||
| Строка 25: | Строка 26: | ||
== Двудольный граф == | == Двудольный граф == | ||
| − | Пусть <tex>G</tex> {{---}} двудольный граф и заданы два матроида <tex>M_1 = \langle X, \mathcal{I}_1 \rangle</tex>, <tex>M_2 = \langle X, \mathcal{I}_2 \rangle</tex>, где <tex>X</tex> {{---}} множество ребёр графа, <tex>\mathcal{I}_1 = \{F \subseteq X: \deg(v) \leqslant 1 \: \forall v \in L \}</tex>, <tex>\mathcal{I}_2 = \{F \subseteq X: \deg(v) \leqslant 1 \: \forall v \in R \}</tex>. Тогда их пересечение {{---}} это множество всевозможных паросочетаний графа. | + | Пусть <tex>G</tex> {{---}} [[Двудольные_графы_и_раскраска_в_2_цвета|двудольный граф]] и заданы два матроида <tex>M_1 = \langle X, \mathcal{I}_1 \rangle</tex>, <tex>M_2 = \langle X, \mathcal{I}_2 \rangle</tex>, где <tex>X</tex> {{---}} множество ребёр графа, <tex>\mathcal{I}_1 = \{F \subseteq X: \deg(v) \leqslant 1 \: \forall v \in L \}</tex>, <tex>\mathcal{I}_2 = \{F \subseteq X: \deg(v) \leqslant 1 \: \forall v \in R \}</tex>. Тогда их пересечение {{---}} это множество всевозможных паросочетаний графа. |
| + | |||
{{Утверждение | {{Утверждение | ||
|statement = | |statement = | ||
| Строка 31: | Строка 33: | ||
|proof = | |proof = | ||
Рассмотрим пару <tex>\langle X, \mathcal{I}\rangle</tex>, <tex>X</tex> {{---}} носитель, <tex> \mathcal{I} = \mathcal{I}_1 \cap \mathcal{I}_2</tex>. | Рассмотрим пару <tex>\langle X, \mathcal{I}\rangle</tex>, <tex>X</tex> {{---}} носитель, <tex> \mathcal{I} = \mathcal{I}_1 \cap \mathcal{I}_2</tex>. | ||
| − | Данная пара не является матроидом, так как не выполняется третье свойство матроида, то есть <tex>\exists A, B \in I, |A| > |B| </tex> и <tex>\nexists \, x \in A \setminus B : B \cup \{x\} \in I</tex> (См. пример 2) | + | Данная пара не является матроидом, так как не выполняется третье свойство матроида, то есть <tex>\exists A, B \in \mathcal{I}, |A| > |B| </tex> и <tex>\nexists \, x \in A \setminus B : B \cup \{x\} \in \mathcal{I}</tex> (См. пример 2) |
[[Файл:Example_DY.png|300px|thumb|left|Пример 2]] | [[Файл:Example_DY.png|300px|thumb|left|Пример 2]] | ||
}} | }} | ||
| − | == | + | == Ориентированный лес == |
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Ориентированное дерево''' (англ. ''arborescence'') {{---}} ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). | + | '''Ориентированное дерево''' (англ. ''arborescence'') {{---}} ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода <tex>1</tex> (в них ведёт ровно по одной дуге). |
| + | }} | ||
| + | Пусть <tex>D = \langle V, X \rangle </tex> {{---}} ориентированнный граф. | ||
| + | Граф <tex>G</tex> {{---}} неориентированный граф, соответствующий графу <tex>D</tex>. | ||
| + | Тогда рассмотрим два матроида <tex>M_1 = \langle X, \mathcal{I}_1 \rangle, M_2 = \langle X, \mathcal{I}_2 \rangle</tex>, где <tex>X</tex> {{---}} множество ребёр графа. | ||
| + | <tex>M_1</tex> {{---}} [[Примеры_матроидов|графовый матроид]] <tex>G</tex>, | ||
| + | <tex>\mathcal{I}_1 = \{X' \subseteq X: X'</tex> {{---}} лес в <tex>G \}</tex>. | ||
| + | <tex>M_2</tex> {{---}} [[Примеры_матроидов|матроид разбиений]] графа <tex>D</tex>, | ||
| + | <tex>\mathcal{I}_2 = \{X' \subseteq X: |\deg^-(v) \cap X'| \leqslant 1, \forall v \in V \}</tex>. | ||
| + | Пересечение данных матроидов являются множества ориентированных лесов. | ||
| + | |||
| + | {{Утверждение | ||
| + | |statement = Пересечение данных матроидов является матроидом. | ||
| + | |proof = | ||
| + | Рассмотрим матроид пересечения <tex>M = \langle X, \mathcal{I} \rangle</tex>, <tex>A</tex> {{---}} множество ребер, <tex>\mathcal{I} = \mathcal{I}_1 \cap \mathcal{I}_2</tex> | ||
| + | |||
| + | Проверим выполнение аксиом независимости: | ||
| + | |||
| + | 1) <tex>\varnothing \in \mathcal{I}</tex> | ||
| + | |||
| + | Пустое множество является ориентированным деревом, а значит входит в <tex>\mathcal{I}</tex>. | ||
| + | |||
| + | 2) <tex>A \subset B, \ B \in \mathcal{I} \Rightarrow A \in \mathcal{I}</tex> | ||
| + | Любой подграф ориентированного леса также является ориентированным лесом, так как во-первых, степень захода каждой вершины в подграфе могла только уменьшится, во-вторых, подграф ацикличного графа {{---}} ацикличен. | ||
| + | |||
| + | 3) <tex>A \in \mathcal{I}, \ B \in I, \ \left\vert A \right\vert < \left\vert B \right\vert \Rightarrow \exists \, x \in B \setminus A, \ A \cup \{ x \} \in \mathcal{I}</tex> | ||
| + | |||
| + | Пусть количество вершин в множестве <tex>A</tex> равно <tex>k</tex>. | ||
| + | Тогда количество ребер в <tex>A</tex> равно <tex>k - 1</tex>. | ||
| + | Так как <tex>|B| > |A|</tex>, следовательно количество ребер в множестве <tex>B</tex> не меньше <tex>k</tex>. | ||
| + | Пусть все ребра из множества <tex>B</tex> ведут в вершины множества <tex>A</tex>, значит в каждую вершину множества <tex>A</tex> входит по одному ребру множества <tex>B</tex>. | ||
| + | Тогда возьмем то ребро, которое указывает в корень (в вершину с нулевой степенью захода), получим ориентированное дерево с новым корнем ('''ну или же получим цикл lol'''). | ||
| + | Пусть не все ребра множества <tex>B</tex> указывают в вершины множества <tex>A</tex>, тогда возьмем то ребро <tex>uv</tex>, которое указывает в вершину не принадлежащую <tex>A</tex>. Покажем, что оно нам подойдет. | ||
| + | Если <tex>u \in V(A)</tex>, тогда наше текущее ориентированное дерево пополнится еще одной вершиной и ведущем к ней ребру. | ||
| + | Если <tex>u \notin V(A)</tex>, то мы получим еще одно ориентированное дерево. | ||
| + | Таким образом, мы нашли ребро в множестве <tex>B \setminus A</tex>, которое можем добавить в множество <tex>A</tex> с сохранением независимости. | ||
| + | |||
| + | }} | ||
| + | |||
| + | {{Утверждение | ||
| + | |statement = Пересечение данных матроидов не является матроидом. | ||
| + | |proof = | ||
| + | Не выполняется третье свойство матроидов, см. пример. | ||
| + | |||
| + | Дан граф <tex>D=(V,X)</tex>, где <tex>V = \{ 1, 2, 3, 4 \}</tex>, а <tex>X = \{ a=(1,2), b=(2,3), c=(3,4), d=(4,2) \}</tex>, тогда достаточно рассмотреть два множества $A=\{ a,b,c \}$ и $B=\{ b,d \}$, чтобы понять, что не выполняется третье свойство матроидов. | ||
}} | }} | ||
| − | |||
== См. также== | == См. также== | ||
| − | * [[ | + | * [[Примеры матроидов]] |
| − | * [[ | + | * [[Алгоритм построения базы в пересечении матроидов]] |
| − | * [[ | + | * [[Алгоритм построения базы в объединении матроидов]] |
==Источники информации == | ==Источники информации == | ||
Текущая версия на 19:15, 4 сентября 2022
| Определение: |
| Пусть даны два матроида и . Пересечением матроидов (англ. matroid intersection) и называется пара , где — носитель исходных матроидов, а . |
- Пересечение матроидов не всегда является матроидом.
- Пересечение трех и более матроидов является NP-полной задачей.
Разноцветный лес
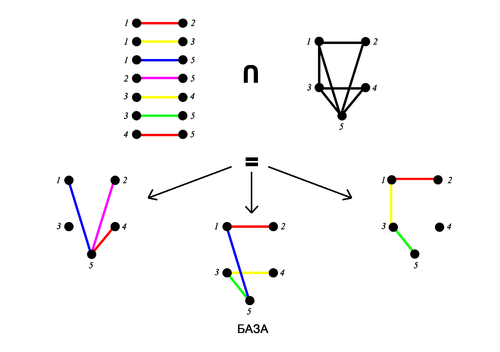
— графовый матроид, — разноцветный матроид (англ. multicolored matroid) (Множество независимо, если в нём нет двух ребер одного цвета). Тогда их пересечение — это разноцветный лес (англ. rainbow forests).
| Утверждение: |
Пересечение данных матроидов не является матроидом. |
|
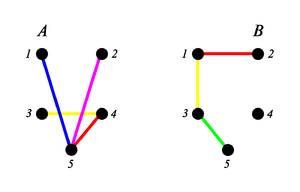
Рассмотрим пару , — ребра разноцветного леса, . Данная пара не является матроидом, так как не выполняется третье свойство матроида, то есть и (См. пример ) |
Двудольный граф
Пусть — двудольный граф и заданы два матроида , , где — множество ребёр графа, , . Тогда их пересечение — это множество всевозможных паросочетаний графа.
| Утверждение: |
Пересечение данных матроидов не является матроидом. |
|
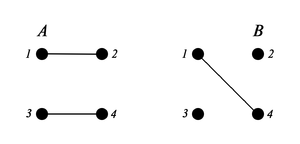
Рассмотрим пару , — носитель, . Данная пара не является матроидом, так как не выполняется третье свойство матроида, то есть и (См. пример 2) |
Ориентированный лес
| Определение: |
| Ориентированное дерево (англ. arborescence) — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода (в них ведёт ровно по одной дуге). |
Пусть — ориентированнный граф. Граф — неориентированный граф, соответствующий графу . Тогда рассмотрим два матроида , где — множество ребёр графа. — графовый матроид , — лес в . — матроид разбиений графа , . Пересечение данных матроидов являются множества ориентированных лесов.
| Утверждение: |
Пересечение данных матроидов является матроидом. |
|
Рассмотрим матроид пересечения , — множество ребер, Проверим выполнение аксиом независимости: 1) Пустое множество является ориентированным деревом, а значит входит в . 2) Любой подграф ориентированного леса также является ориентированным лесом, так как во-первых, степень захода каждой вершины в подграфе могла только уменьшится, во-вторых, подграф ацикличного графа — ацикличен. 3) Пусть количество вершин в множестве равно . Тогда количество ребер в равно . Так как , следовательно количество ребер в множестве не меньше . Пусть все ребра из множества ведут в вершины множества , значит в каждую вершину множества входит по одному ребру множества . Тогда возьмем то ребро, которое указывает в корень (в вершину с нулевой степенью захода), получим ориентированное дерево с новым корнем (ну или же получим цикл lol). Пусть не все ребра множества указывают в вершины множества , тогда возьмем то ребро , которое указывает в вершину не принадлежащую . Покажем, что оно нам подойдет. Если , тогда наше текущее ориентированное дерево пополнится еще одной вершиной и ведущем к ней ребру. Если , то мы получим еще одно ориентированное дерево. Таким образом, мы нашли ребро в множестве , которое можем добавить в множество с сохранением независимости. |
| Утверждение: |
Пересечение данных матроидов не является матроидом. |
|
Не выполняется третье свойство матроидов, см. пример. Дан граф , где , а , тогда достаточно рассмотреть два множества $A=\{ a,b,c \}$ и $B=\{ b,d \}$, чтобы понять, что не выполняется третье свойство матроидов. |
См. также
Источники информации
- Асанов М. О., Баранский В. А., Расин В. В. — Дискретная математика: Графы, матроиды, алгоритмы (глава 4. Матроиды)
- Lecture notes on matroid intersection