Производящие функции нескольких переменных — различия между версиями
Ivan (обсуждение | вклад) (sta) |
(sta) |
||
| Строка 1: | Строка 1: | ||
| − | Обычные [[Производящая функция | Производящие функции ]] хранили одну последовательность чисел. Для задач, которые требуют больше информации применяются ''' | + | Обычные [[Производящая функция | Производящие функции ]] хранили одну последовательность чисел. Для задач, которые требуют больше информации применяются '''производящие функции нескольких переменных''' (англ. ''multivariable generating function''). Очень часто применяются функции от двух переменных(далее они и будут рассматриваться), которые в общем случае принимают вид |
| + | <center> | ||
| + | <tex>G(x, y) = \sum\limits_{n, k \geqslant 0} g_{n, k} x^n y^k</tex> | ||
| + | </center> | ||
| + | |||
| + | Такие последовательности удобно задавать в виде треугольника. Рассмотрим несколько примеров : | ||
== Треугольник Паскаля == | == Треугольник Паскаля == | ||
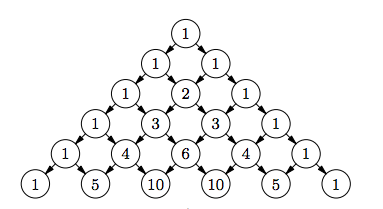
| − | [[File:Pascal_triangle.png|thumb|400px| | + | [[File:Pascal_triangle.png|thumb|400px|center|Рис.<tex>1</tex>]] |
| − | Треугольник Паскаля | + | Треугольник Паскаля (рис.<tex>1</tex>). Элементы треугольника перечисляют пути, идущие из его вершины в соответствующую клетку. Пути имеют вид ломаных, составленных из векторов единичной длины двух видов: идущих вправо-вниз и идущих влево-вниз. |
| − | Числа, стоящие в треугольнике - биномиальные коэффициенты <tex> c_{n,k} = \begin{pmatrix} n \\ k \end{pmatrix}</tex>. Кратко докажем (индукция по n) . Предположим, что числа в <tex>n | + | {{Теорема |
| + | |statement= Числа, стоящие в треугольнике - биномиальные коэффициенты <tex> c_{n,k} = \begin{pmatrix} n \\ k \end{pmatrix}</tex>. | ||
| + | |proof= Числа, стоящие в треугольнике - биномиальные коэффициенты <tex> c_{n,k} = \begin{pmatrix} n \\ k \end{pmatrix}</tex>. Кратко докажем (индукция по n) . Предположим, что числа в <tex>n</tex>-ой строчке треугольника совпадают с коэффициентами разложения многочлена <tex>(1 + s)^{n}</tex>. число различных путей, ведущих в точку <tex>(n + 1, k)</tex>, равно сумме числа путей, ведущих в точку <tex>(n, k - 1)</tex>, и числа путей, ведущих в точку <tex>(n, k)</tex> , <tex>c_{n+1,k} = c_{n,k-1} + c_{n,k}</tex>. Поэтому число <tex>c_{n+1, k}</tex> совпадает с коэффициентом при <tex>s^k</tex> в многочлене <tex>(1+s) \cdot (1+s)^n = | ||
(1+s)^{n+1}</tex>. | (1+s)^{n+1}</tex>. | ||
| + | |||
| + | }} | ||
| + | |||
Производящая функция может быть сопоставлена треугольнику Паскаля несколькими способами. Например, можно рассмотреть производящую функцию | Производящая функция может быть сопоставлена треугольнику Паскаля несколькими способами. Например, можно рассмотреть производящую функцию | ||
| + | <tex>\sum\limits_{n,k = 0}^{\infty} c_{n,k} x^k y^n = \sum\limits_{n,k = 0}^{\infty} \begin{pmatrix} n \\ k \end{pmatrix} x^k y^n = \sum\limits_{n = 0}^{\infty}\Big(\sum\limits_{k = 0}^{n} \begin{pmatrix} n \\ k \end{pmatrix} x^k\Big) y^n = \sum\limits_{n = 0}^{\infty} (1 + x)^n y^n = \dfrac{1}{1 - y - xy}</tex> | ||
| − | <tex> | + | [[File:Pascal_triangle_3.png|thumb|600px|right|Рис.<tex>2</tex>]] |
| − | + | Второй способ соответсвует нумерации элементов треугольника числом отрезков каждого типа на путях, ведущих в соответствующую точку (рис.<tex>2</tex>) <tex>C_{n,m} = c_{n+m, n} = \begin{pmatrix} n + m \\ m \end{pmatrix}</tex>. Тогда производящая функция будет иметь вид | |
| − | |||
| − | Второй способ соответсвует нумерации элементов треугольника числом отрезков каждого типа на путях, ведущих в соответствующую точку (рис.2) <tex>C_{n,m} = c_{n+m, n} = \begin{pmatrix} n + m \\ m \end{pmatrix}</tex>. Тогда производящая функция будет иметь вид | ||
<tex>\sum\limits_{n,m = 0}^{\infty} C_{n, m} x^n y^m = \sum\limits_{n,m = 0}^{\infty} \begin{pmatrix} n + m \\ m \end{pmatrix} x^n y^m = \sum\limits_{k = 0}^{\infty} \sum\limits_{n + m = k} \begin{pmatrix} n + m \\ n \end{pmatrix} | <tex>\sum\limits_{n,m = 0}^{\infty} C_{n, m} x^n y^m = \sum\limits_{n,m = 0}^{\infty} \begin{pmatrix} n + m \\ m \end{pmatrix} x^n y^m = \sum\limits_{k = 0}^{\infty} \sum\limits_{n + m = k} \begin{pmatrix} n + m \\ n \end{pmatrix} | ||
| − | x^n y^m = \sum\limits_{k = 0}^{\infty} (x + y)^k = \ | + | x^n y^m = \sum\limits_{k = 0}^{\infty} (x + y)^k = \dfrac{1}{1 -x - y}</tex> |
| − | Также существует еще один способ: сопоставить треугольнику Паскаля | + | Также существует еще один способ: сопоставить треугольнику Паскаля ''экспоненциальную производящую функцию''. Экспоненциальная производящая функция отличается от обычной тем, что в качестве коэффициентов степенного ряда берутся не элементы последовательности <tex>a_n</tex>, а числа <tex>\dfrac{a_n}{n!}</tex> |
==Экспоненциальные производящие функции== | ==Экспоненциальные производящие функции== | ||
| Строка 30: | Строка 39: | ||
<tex>\{ \alpha_n \} \mapsto \sum\limits_{n = 0}^{\infty} a_n \alpha_n s^n</tex> | <tex>\{ \alpha_n \} \mapsto \sum\limits_{n = 0}^{\infty} a_n \alpha_n s^n</tex> | ||
| − | определяемую последовательностью <tex>\{ \alpha_n \}</tex>. Если в последовательности <tex>\{ \alpha_n \}</tex> отсутствуют нулевые элементы, то такое сопоставление взаимно однозначно. До сих пор мы пользовались обычными производящими функциями - отвечающими последовательности <tex>\{ \alpha_n \} \equiv 1</tex>. В зависимости от преследуемых целей целей могут принести и другие последовательности | + | определяемую последовательностью <tex>\{ \alpha_n \}</tex>. Если в последовательности <tex>\{ \alpha_n \}</tex> отсутствуют нулевые элементы, то такое сопоставление взаимно однозначно. До сих пор мы пользовались обычными производящими функциями - отвечающими последовательности <tex>\{ \alpha_n \} \equiv 1</tex>. В зависимости от преследуемых целей целей могут принести и другие последовательности . |
| − | + | {{Определение | |
| + | |definition= | ||
| + | '''Производящие экспоненциальные функции'''(англ. ''exponential generating function'') - функции, соответсвующие последовательности <tex>\{ \alpha_n \} = \dfrac{1}{n!}</tex>. | ||
| + | }} | ||
| − | <tex>\sum\limits_{n = 0}^{\infty} \ | + | {{Определение |
| + | |definition= | ||
| + | Экспоненциальные производящие функции для целочисленных последовательностей называют '''функциями Гурвица'''(англ. ''Hurwitz function''). | ||
| + | }} | ||
| + | |||
| + | Чем отличаются экспоненциальные производящие функции от обычных? Посмотрим на поведение экспоненциальных производящих функций при выполнении операции над ними. Сумма ведет себя обычным образом: | ||
| + | |||
| + | <tex>\sum\limits_{n = 0}^{\infty} \dfrac{a_n}{n!}s^n + \sum\limits_{n = 0}^{\infty} \dfrac{b+n}{n!}s^n = \sum\limits_{n = 0}^{\infty} \dfrac{(a_n + b_n)}{n!} s^n</tex> | ||
а с произведением по-другому : | а с произведением по-другому : | ||
| − | <tex>(\ | + | <tex>\bigg(\dfrac{a_0}{0!} + \dfrac{a_1}{1!}s + \dfrac{a_2}{2!}s^2 + \ldots\bigg)\bigg(\dfrac{b_0}{0!} + \dfrac{b_1}{1!}s + \dfrac{b_2}{2!}s^2 + \ldots\bigg) = \dfrac{a_0}{0!} \dfrac{b_0}{0!} + \bigg(\dfrac{a_0}{0!} \dfrac{b_1}{1!} + \dfrac{a_1}{1!} \dfrac{b_0}{0!}\bigg)s + \bigg(\dfrac{a_0}{0!} \dfrac{b_2}{2!} + \dfrac{a_1}{1!} \dfrac{b_1}{1!} + \dfrac{a_2}{2!} \dfrac{b_0}{0!}\bigg)s^2 + \ldots</tex> |
| − | Коэффициенты <tex>\ | + | Коэффициенты <tex>\dfrac{c_n}{n!}</tex> произведения вычисляются по формуле |
| − | <tex>c_n = \begin{pmatrix} n \\ 0 \end{pmatrix} a_0 b_n + \begin{pmatrix} n \\ 1 \end{pmatrix} a_1 b_{n - 1} + \ | + | <tex>c_n = \begin{pmatrix} n \\ 0 \end{pmatrix} a_0 b_n + \begin{pmatrix} n \\ 1 \end{pmatrix} a_1 b_{n - 1} + \ldots + \begin{pmatrix} n \\ n \end{pmatrix} a_0 b_0</tex> |
Еще одно существенное отличие экспоненциальных производящих функций от обычных наблюдается при взятии производных (и интегрировании). Дифференцирование или интегрирование экспоненциальной производящей функции приводит к сдвигу последовательности ее коэффициентов без изменения их велечины : | Еще одно существенное отличие экспоненциальных производящих функций от обычных наблюдается при взятии производных (и интегрировании). Дифференцирование или интегрирование экспоненциальной производящей функции приводит к сдвигу последовательности ее коэффициентов без изменения их велечины : | ||
| − | <tex>( \ | + | <tex>\bigg( \dfrac{a_0}{0!} + \dfrac{a_1}{1!}s + \dfrac{a_2}{2!}s^2 + \ldots \bigg)^{'} = \dfrac{a_1}{0!} + \dfrac{a_2}{1!}s + \dfrac{a_3}{2!}s^2 + \ldots </tex> |
| − | <tex>\int (\ | + | <tex>\int \bigg(\dfrac{a_0}{0!} + \dfrac{a_1}{1!}s + \dfrac{a_2}{2!}s^2 + \ldots \bigg) = \dfrac{a_0}{1!}s + \dfrac{a_1}{2!}s^2 + \dfrac{a_2}{3!}s^3 + \dfrac{a_3}{4!}s^4 + \ldots </tex> |
| − | Обычная производящая функция <tex>A(s) = a_0 + a_1s + a_2s^2 + \ | + | Обычная производящая функция <tex>A(s) = a_0 + a_1s + a_2s^2 + \ldots</tex> выражается через экспоненциальную <tex>\mathcal{A} (t) = \dfrac{a_0}{0!} + \dfrac{a_1}{1!}t + \dfrac{a_2}{2!}t^2 + \ldots </tex> по формуле |
<tex>A(s) = \int_{0}^{\infty} e^{-t} \mathcal{A}(st) dt</tex> | <tex>A(s) = \int_{0}^{\infty} e^{-t} \mathcal{A}(st) dt</tex> | ||
| Строка 60: | Строка 79: | ||
Теперь можно выписать экспоненциальную производящую функцию для треугольника Паскаля : | Теперь можно выписать экспоненциальную производящую функцию для треугольника Паскаля : | ||
| − | <tex>\sum\limits_{n, m = 0}^{\infty} \ | + | <tex>\sum\limits_{n, m = 0}^{\infty} \dfrac{1}{(n + m)!} \begin{pmatrix} n + m \\ m \end{pmatrix} x^n y^m = \sum\limits_{n = 0}^{\infty} \dfrac{(x + y)^n}{n!} = e^{x + y}</tex> |
==Треугольник Дика== | ==Треугольник Дика== | ||
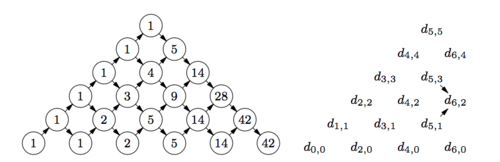
| − | [[File:Triangle_D_2.png|thumb|500px|right|Рис.3 Представление треугольника Дика]] | + | [[File:Triangle_D_2.png|thumb|500px|right|Рис.<tex>3</tex> Представление треугольника Дика]] |
| − | Треугольник Дика перечисляет пути в положительном квадранте плоскости, выходящие из начала координат и составленные из векторов <tex>(1, 1)</tex> и <tex>(1, -1)</tex> (рис.3). Мы можем увидеть, что элементы <tex>d_{ij}</tex> треугольника Дика отличны от нуля в том и только том случае, если <tex>i \ | + | Треугольник Дика перечисляет пути в положительном квадранте плоскости, выходящие из начала координат и составленные из векторов <tex>(1, 1)</tex> и <tex>(1, -1)</tex> (рис.<tex>3</tex>). Мы можем увидеть, что элементы <tex>d_{ij}</tex> треугольника Дика отличны от нуля в том и только том случае, если <tex>i \geqslant j </tex> и <tex>i + j</tex> четно. Обозначим через <tex>D(x, y)</tex> производящую функцию Дика двух пременных |
<tex>D(x, y) = \sum\limits_{i,j =0}^{\infty} d_{ij} x^i y^j</tex> | <tex>D(x, y) = \sum\limits_{i,j =0}^{\infty} d_{ij} x^i y^j</tex> | ||
| Строка 72: | Строка 91: | ||
Правило построения треугольника Дика подсказывает нам уравнение на эту производящую функцию | Правило построения треугольника Дика подсказывает нам уравнение на эту производящую функцию | ||
| − | <tex>xyD(x, y) + (D(x,y) - D(x,0))\ | + | <tex>xyD(x, y) + (D(x,y) - D(x,0))\dfrac{x}{y} = D(x, y) - 1</tex> |
| + | |||
| + | Действительно, коэффициент при любом мономе <tex>x^iy^j</tex> , отличном от единичного, представляет собой сумму коэффициентов при мономах <tex>x^{i-1}y^{i-1}</tex> и <tex>x^{i-1}y^{j+1}</tex> . Функция <tex>D(x, 0) = \dfrac{1 - \sqrt{1 - 4x^2}}{2x^2}</tex> нам известна, и ряд <tex>D(x, y)</tex> находится решением линейного уравнения, | ||
| − | + | <tex>D(x, y) = \dfrac{1 - \sqrt{1 - 4x^2} - 2xy}{2x(xy^2 + x - y)}</tex> | |
| − | + | ==См. также== | |
| + | *[[Производящая функция]] | ||
==Источники информации== | ==Источники информации== | ||
| − | * Ландо. Лекции о производящих функциях | + | * ''Ландо С.К.'' ''Лекции о производящих функциях'' {{---}} МЦНМО, 2007 - С. 57 |
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Комбинаторика]] | [[Категория: Комбинаторика]] | ||
[[Категория: Подсчёт числа объектов]] | [[Категория: Подсчёт числа объектов]] | ||
Версия 01:39, 25 мая 2017
Обычные Производящие функции хранили одну последовательность чисел. Для задач, которые требуют больше информации применяются производящие функции нескольких переменных (англ. multivariable generating function). Очень часто применяются функции от двух переменных(далее они и будут рассматриваться), которые в общем случае принимают вид
Такие последовательности удобно задавать в виде треугольника. Рассмотрим несколько примеров :
Содержание
Треугольник Паскаля
Треугольник Паскаля (рис.). Элементы треугольника перечисляют пути, идущие из его вершины в соответствующую клетку. Пути имеют вид ломаных, составленных из векторов единичной длины двух видов: идущих вправо-вниз и идущих влево-вниз.
| Теорема: |
Числа, стоящие в треугольнике - биномиальные коэффициенты . |
| Доказательство: |
| Числа, стоящие в треугольнике - биномиальные коэффициенты . Кратко докажем (индукция по n) . Предположим, что числа в -ой строчке треугольника совпадают с коэффициентами разложения многочлена . число различных путей, ведущих в точку , равно сумме числа путей, ведущих в точку , и числа путей, ведущих в точку , . Поэтому число совпадает с коэффициентом при в многочлене . |
Производящая функция может быть сопоставлена треугольнику Паскаля несколькими способами. Например, можно рассмотреть производящую функцию
Второй способ соответсвует нумерации элементов треугольника числом отрезков каждого типа на путях, ведущих в соответствующую точку (рис.) . Тогда производящая функция будет иметь вид
Также существует еще один способ: сопоставить треугольнику Паскаля экспоненциальную производящую функцию. Экспоненциальная производящая функция отличается от обычной тем, что в качестве коэффициентов степенного ряда берутся не элементы последовательности , а числа
Экспоненциальные производящие функции
Зафиксируем произвольную последовательность . Каждой последовательности мы можем сопоставить производящую функцию
определяемую последовательностью . Если в последовательности отсутствуют нулевые элементы, то такое сопоставление взаимно однозначно. До сих пор мы пользовались обычными производящими функциями - отвечающими последовательности . В зависимости от преследуемых целей целей могут принести и другие последовательности .
| Определение: |
| Производящие экспоненциальные функции(англ. exponential generating function) - функции, соответсвующие последовательности . |
| Определение: |
| Экспоненциальные производящие функции для целочисленных последовательностей называют функциями Гурвица(англ. Hurwitz function). |
Чем отличаются экспоненциальные производящие функции от обычных? Посмотрим на поведение экспоненциальных производящих функций при выполнении операции над ними. Сумма ведет себя обычным образом:
а с произведением по-другому :
Коэффициенты произведения вычисляются по формуле
Еще одно существенное отличие экспоненциальных производящих функций от обычных наблюдается при взятии производных (и интегрировании). Дифференцирование или интегрирование экспоненциальной производящей функции приводит к сдвигу последовательности ее коэффициентов без изменения их велечины :
Обычная производящая функция выражается через экспоненциальную по формуле
Действительно,
Теперь можно выписать экспоненциальную производящую функцию для треугольника Паскаля :
Треугольник Дика
Треугольник Дика перечисляет пути в положительном квадранте плоскости, выходящие из начала координат и составленные из векторов и (рис.). Мы можем увидеть, что элементы треугольника Дика отличны от нуля в том и только том случае, если и четно. Обозначим через производящую функцию Дика двух пременных
Правило построения треугольника Дика подсказывает нам уравнение на эту производящую функцию
Действительно, коэффициент при любом мономе , отличном от единичного, представляет собой сумму коэффициентов при мономах и . Функция нам известна, и ряд находится решением линейного уравнения,
См. также
Источники информации
- Ландо С.К. Лекции о производящих функциях — МЦНМО, 2007 - С. 57