Раскраска графа — различия между версиями
(→Раскраска графа) |
Roman (обсуждение | вклад) |
||
| (не показаны 4 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
{{Определение | {{Определение | ||
| − | |definition= '''Правильной раскраской | + | |definition= '''Правильной раскраской''' (англ. ''Regular coloring'') графа <tex>G(V,E)</tex> называется такое отображение <tex>\varphi</tex> из множества вершин <tex>V</tex> в множество красок <tex>\{c_1 \ldots c_t\}</tex>, что для любых двух смежных вершин <tex>u</tex> и <tex>v</tex> выполняется <tex>\varphi(u)\ne\varphi(v)</tex>. Так же её называют '''<tex>t</tex>-раскраской'''. |
}} | }} | ||
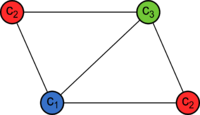
[[Файл:Paint.png|200px|thumb|center|Пример раскраски графа из четырех вершин.]] | [[Файл:Paint.png|200px|thumb|center|Пример раскраски графа из четырех вершин.]] | ||
| Строка 8: | Строка 6: | ||
Раскраской графа чаще всего называют именно правильную раскраску. | Раскраской графа чаще всего называют именно правильную раскраску. | ||
| − | |||
| − | == | + | Первоначально раскраски графов были нужны для составления географических карт<ref name="4problem"> [http://ru.wikipedia.org/wiki/Проблема_четырёх_красок Проблема четырёх красок]</ref>. Сегодня же они (в частности раскраска с использованием минимального количества цветов) используются, например, для составления расписаний, распределения регистров в микропроцессорах, распараллеливания численных методов.<ref name="pract">[http://ru.wikipedia.org/wiki/Практическое_применение_раскраски_графов Практическое применение раскраски графов]</ref> |
| + | |||
| + | ==Хроматические числа различных графов== | ||
{{Определение | {{Определение | ||
| − | |definition= '''Хроматическим числом''' <tex>\chi(G)</tex> графа <tex>G(V,E)</tex> называется такое минимальное число <tex>t</tex>, для которого существует <tex>t</tex>-раскраска графа. | + | |id= chromatic_number_difinition |
| + | |definition= '''Хроматическим числом''' (англ. ''Chromatic number'') <tex>\chi(G)</tex> графа <tex>G(V,E)</tex> называется такое минимальное число <tex>t</tex>, для которого существует <tex>t</tex>-раскраска графа. | ||
}} | }} | ||
| − | + | * <tex>1</tex>-хроматические графы {{---}} это нулевые(не имеющие ребер) графы и только они. <tex>\chi(O_{n}) = 1</tex>. | |
| − | |||
| − | + | * <tex>\chi(K_{n}) = n</tex> {{---}} хроматическое число полного графа равно <tex>n</tex>. | |
| − | + | * <tex>\chi(C_{n}) = | |
\begin{cases} | \begin{cases} | ||
2\text{, if $n$ is even;}\\ | 2\text{, if $n$ is even;}\\ | ||
| Строка 27: | Строка 26: | ||
</tex> | </tex> | ||
| − | + | * <tex>G = (V, E)</tex> {{---}} двудольный граф, тогда <tex>\chi(G) = 2</tex> | |
| − | Задача о нахождении <tex>\chi(G)</tex> не разрешима за полиномиальное время. | + | Задача о нахождении <tex>\chi(G)</tex> [[NP-полнота_задачи_о_раскраске_графа | не разрешима за полиномиальное время]]. |
| − | == Хроматический многочлен == | + | ==Хроматический многочлен== |
{{main|Хроматический многочлен}} | {{main|Хроматический многочлен}} | ||
{{Определение | {{Определение | ||
| − | |definition= | + | |definition='''Хроматический многочлен''' (англ. ''Chromatic polynomial'') <tex>P(G, t)</tex> {{---}} число способов раскрасить граф <tex>G</tex> в <tex>t</tex> цветов. |
}} | }} | ||
| − | == Источники == | + | ==Связь хроматического числа и хроматического многочлена== |
| − | + | *Минимальное натуральное число, на котором хроматический многочлен для данного графа принимает натуральное значение, является хроматическим числом для данного графа. Поэтому если известен хроматический многочлен, то хроматическое число можно определить последовательной подстановкой. Однако задача о нахождении хроматического многочлена также не разрешима за полиномиальное время. | |
| − | + | *В обратную сторону, т.е. если известно хроматическое число, построить хроматический многочлен не получится. Так как оно не дает почти никакой информации о структуре графа. | |
| + | |||
| + | ==Примечания== | ||
| + | <references/> | ||
| + | |||
| + | ==Источники информации== | ||
| + | * Асанов М. О., Баранский В. А., Расин В. В. {{---}} Дискретная математика: Графы, матроиды, алгоритмы. '''ISBN 978-5-8114-1068-2'''<br /> | ||
| + | * Харари Ф. {{---}} Теория графов. '''ISBN 978-5-397-00622-4''' | ||
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Раскраски графов]] | [[Категория: Раскраски графов]] | ||
Версия 16:47, 8 ноября 2015
| Определение: |
| Правильной раскраской (англ. Regular coloring) графа называется такое отображение из множества вершин в множество красок , что для любых двух смежных вершин и выполняется . Так же её называют -раскраской. |
Раскраской графа чаще всего называют именно правильную раскраску.
Первоначально раскраски графов были нужны для составления географических карт[1]. Сегодня же они (в частности раскраска с использованием минимального количества цветов) используются, например, для составления расписаний, распределения регистров в микропроцессорах, распараллеливания численных методов.[2]
Содержание
Хроматические числа различных графов
| Определение: |
| Хроматическим числом (англ. Chromatic number) графа называется такое минимальное число , для которого существует -раскраска графа. |
- -хроматические графы — это нулевые(не имеющие ребер) графы и только они. .
- — хроматическое число полного графа равно .
- — двудольный граф, тогда
Задача о нахождении не разрешима за полиномиальное время.
Хроматический многочлен
| Определение: |
| Хроматический многочлен (англ. Chromatic polynomial) — число способов раскрасить граф в цветов. |
Связь хроматического числа и хроматического многочлена
- Минимальное натуральное число, на котором хроматический многочлен для данного графа принимает натуральное значение, является хроматическим числом для данного графа. Поэтому если известен хроматический многочлен, то хроматическое число можно определить последовательной подстановкой. Однако задача о нахождении хроматического многочлена также не разрешима за полиномиальное время.
- В обратную сторону, т.е. если известно хроматическое число, построить хроматический многочлен не получится. Так как оно не дает почти никакой информации о структуре графа.
Примечания
Источники информации
- Асанов М. О., Баранский В. А., Расин В. В. — Дискретная математика: Графы, матроиды, алгоритмы. ISBN 978-5-8114-1068-2
- Харари Ф. — Теория графов. ISBN 978-5-397-00622-4