Реализация запроса в дереве отрезков сверху — различия между версиями
Gr1n (обсуждение | вклад) (→Алгоритм) |
(Лишний пробел) |
||
| (не показано 48 промежуточных версий 8 участников) | |||
| Строка 3: | Строка 3: | ||
==Алгоритм== | ==Алгоритм== | ||
''Замечание.'' | ''Замечание.'' | ||
| − | Используем в алгоритме не отрезки, а полуинтервалы(левая граница включительно, а правая - нет). | + | Используем в алгоритме не отрезки, а полуинтервалы (левая граница включительно, а правая {{---}} нет). |
| − | Пусть есть уже [[Дерево отрезков. Построение|построенное дерево отрезков]] и идет запрос на полуинтервале <tex>[a | + | Пусть есть уже [[Дерево отрезков. Построение|построенное дерево отрезков]] и идет запрос на полуинтервале <tex>[a \ldots b)</tex>. |
| − | |||
В качестве параметров рекурсий передаем следующие переменные: | В качестве параметров рекурсий передаем следующие переменные: | ||
| − | * <tex>node</tex> {{---}} номер(в массиве с деревом отрезков) текущей вершины дерева. | + | * <tex>node</tex> {{---}} номер (в массиве с деревом отрезков) текущей вершины дерева. |
* <tex>a</tex>, <tex>b</tex> {{---}} левая и правая границы запрашиваемого полуинтервала. | * <tex>a</tex>, <tex>b</tex> {{---}} левая и правая границы запрашиваемого полуинтервала. | ||
| − | Пусть <tex>l</tex>, <tex>r</tex> {{---}} это левая и правая границы полуинтервала, за которые "отвечает" наша | + | Пусть <tex>l</tex>, <tex>r</tex> {{---}} это левая и правая границы полуинтервала, за которые "отвечает" наша вершина. |
| + | Запустим рекурсивную процедуру от всего полуинтервала (то есть от корневой вершины). | ||
| − | + | Для текущего состояния проверяем следующие условия: | |
| − | + | * Если текущий полуинтервал не пересекается с искомым, то возвращаем нейтральный элемент. | |
| + | :''Например'': текущий <tex>[1 \ldots 3)</tex>, а искомый <tex>[3 \ldots 5)</tex>; | ||
| − | * Если текущий полуинтервал | + | * Если текущий полуинтервал лежит внутри запрашиваемого полуинтервала, то возвращаем значение в текущей вершине. |
| − | ''Например'': текущий <tex>[ | + | :''Например'': текущий <tex>[2 \ldots 3)</tex>, а искомый <tex>[2 \ldots 4)</tex>; |
| − | * | + | * Иначе переходим к рекурсивным вызовам функций от детей вершины. При этом возвращаем значение на текущем полуинтервале, как функцию (соответствующую типу нашего запроса) от результатов выполнения на детях. |
| − | |||
| − | + | Так как на каждом уровне дерева рекурсия может дойти до не более, чем двух вершин (иначе бы нашлось две рядом стоящие вершины одного уровня, объединение которых дало отрезок, за который отвечает вершина предыдущего уровня), а всего уровней <tex>\log n</tex>, то операция выполняется за <tex>O(\log n)</tex>. | |
| − | |||
| − | + | ==Пример== | |
| − | + | Рассмотрим данный алгоритм на примере задачи <tex>\mathrm{RSQ}</tex> (Range Sum Query {{---}} запрос суммы на отрезке). | |
| − | |||
| − | |||
| − | |||
| − | При этом сумма на текущем полуинтервале(в случае вызова рекурсий от детей) равна сумме результатов выполнения | + | При этом сумма на текущем полуинтервале (в случае вызова рекурсий от детей) равна сумме результатов выполнения операции на этих детях. |
Пусть дерево содержит <tex>8</tex> листьев и запрашиваемая сумма | Пусть дерево содержит <tex>8</tex> листьев и запрашиваемая сумма | ||
| − | {{---}} это отрезок <tex>[1 | + | {{---}} это отрезок <tex>[1 \ldots 4]</tex> (полуинтервал <tex>[1 \ldots 5)</tex>). |
| + | [[Файл:Image_4.png|right|602px|Пример рабoты алгоритма]] | ||
| + | Рассмотрим данный алгоритм на определенных глубинах рекурсии, то есть на разных уровнях дерева (на рисунке глубина обозначена слева от уровня): | ||
| − | + | * На глубине <tex>0</tex>. | |
| + | ** Текущий полуинтервал <tex>[0 \ldots 8)</tex> пересекается с <tex>[1 \ldots 5) \Rightarrow</tex> рекурсивно переходим к <tex>[0 \ldots 4)</tex> и <tex>[4 \ldots 8)</tex> | ||
| − | |||
| + | * На глубине <tex>1</tex>. | ||
| + | ** <tex>[0 \ldots 4)</tex> и <tex>[4 \ldots 8)</tex> пересекаются с <tex> [1 \ldots 5) \Rightarrow </tex> переходим по рекурсивным вызовам на полуинтервалах <tex>[0 \ldots | ||
| + | 2)</tex>, <tex>[2 \ldots 4)</tex>, <tex>[4 \ldots 6)</tex> и <tex>[6 \ldots 8)</tex> | ||
| − | |||
| + | * На глубине <tex>2</tex>. | ||
| + | ** <tex>[0 \ldots 2)</tex> и <tex>[4 \ldots 6)</tex> пересекаются с <tex>[1 \ldots 5) \Rightarrow </tex> переходим в листья <tex>[0 \ldots 1), [1 \ldots 2), [4 \ldots 5), [5 \ldots 6) </tex> | ||
| + | ** <tex>[2 \ldots 4) </tex> полностью лежит внутри <tex>[1 \ldots 5) \Rightarrow </tex> возвращаем сумму на этом отрезке | ||
| + | ** <tex>[6 \ldots 8)</tex> не пересекается с <tex>[1 \ldots 5) \Rightarrow </tex> возвращаем нулевое значение | ||
| − | |||
| + | * На глубине <tex>3</tex>. | ||
| + | ** Листья <tex>[1 \ldots 2), [4 \ldots 5)</tex> лежат в запрашиваемом интервале <tex>\Rightarrow </tex> возвращаем значения в них | ||
| + | ** Листья <tex>[0 \ldots 1), [5 \ldots 6)</tex> лежат вне <tex>[1 \ldots 5) \Rightarrow </tex> возвращаем нейтральное значение | ||
| − | + | Таким образом ответ на полуинтервале <tex>[1 \ldots 5)</tex> равен сумме значений в вершинах, отвечающих за полуинтервалы <tex>[1 \ldots 2)</tex>, <tex>[2 \ldots 4)</tex> и <tex>[4 \ldots 5)</tex>. | |
==Реализация== | ==Реализация== | ||
| − | Рассмотрим реализацию задачи | + | Рассмотрим реализацию задачи о дереве отрезков с произвольной ассоциативной бинарной операцией. |
| − | |||
| − | + | Пусть в узлах дерева хранятся структуры из трех полей: | |
| − | + | * <tex>\mathtt{left}</tex> {{---}} левая граница полуинтервала, за который "отвечает" текущая вершина. | |
| − | + | * <tex>\mathtt{right}</tex> {{---}} правая граница этого полуинтервала. | |
| − | + | * <tex> \mathtt{res}</tex> {{---}} результат операции на полуинтервале. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | '''int''' query('''int''' node, '''int''' a, '''int''' b) |
| + | l = tree[node].left | ||
| + | r = tree[node].right | ||
| + | '''if''' [l, r) <tex>\cap </tex> [a, b) == <tex>\varnothing</tex> | ||
| + | '''return''' ''<tex>\varepsilon</tex>'' <span style="color:#008000">// <tex>\varepsilon</tex> {{---}} нейтральный для данной операции элемент</span> | ||
| + | '''if''' [l, r) <tex>\subset</tex> [a, b) | ||
| + | '''return''' tree[node].res | ||
| + | '''return''' query(node * 2 + 1, a, b) <tex> \circ </tex> query(node * 2 + 2, a, b) | ||
| − | [ | + | ==См. также== |
| + | * [[Реализация запроса в дереве отрезков снизу]] | ||
| + | * [[Дерево отрезков. Построение]] | ||
| − | [http://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D0%BE%D1%82%D1%80%D0%B5%D0%B7%D0%BA%D0%BE%D0%B2 Дерево отрезков | + | ==Источники информации== |
| + | * [http://e-maxx.ru/algo/segment_tree MAXimal :: algo :: Дерево отрезков] | ||
| + | * [http://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D0%BE%D1%82%D1%80%D0%B5%D0%B7%D0%BA%D0%BE%D0%B2 Википедия — Дерево отрезков] | ||
| − | [http://rain.ifmo.ru/cat/view.php/vis/trees/segment-2006 Визуализатор дерева отрезков] | + | * [http://rain.ifmo.ru/cat/view.php/vis/trees/segment-2006 Дискретная математика: Алгоритмы — Визуализатор дерева отрезков] |
[[Категория: Дискретная математика и алгоритмы]] | [[Категория: Дискретная математика и алгоритмы]] | ||
[[Категория: Дерево отрезков]] | [[Категория: Дерево отрезков]] | ||
Версия 22:14, 5 сентября 2019
Данная операция позволяет выполнять запросы на дереве отрезков, причем алгоритм запускается от корня и рекурсивно идет сверху вниз.
Алгоритм
Замечание. Используем в алгоритме не отрезки, а полуинтервалы (левая граница включительно, а правая — нет).
Пусть есть уже построенное дерево отрезков и идет запрос на полуинтервале .
В качестве параметров рекурсий передаем следующие переменные:
- — номер (в массиве с деревом отрезков) текущей вершины дерева.
- , — левая и правая границы запрашиваемого полуинтервала.
Пусть , — это левая и правая границы полуинтервала, за которые "отвечает" наша вершина. Запустим рекурсивную процедуру от всего полуинтервала (то есть от корневой вершины).
Для текущего состояния проверяем следующие условия:
- Если текущий полуинтервал не пересекается с искомым, то возвращаем нейтральный элемент.
- Например: текущий , а искомый ;
- Если текущий полуинтервал лежит внутри запрашиваемого полуинтервала, то возвращаем значение в текущей вершине.
- Например: текущий , а искомый ;
- Иначе переходим к рекурсивным вызовам функций от детей вершины. При этом возвращаем значение на текущем полуинтервале, как функцию (соответствующую типу нашего запроса) от результатов выполнения на детях.
Так как на каждом уровне дерева рекурсия может дойти до не более, чем двух вершин (иначе бы нашлось две рядом стоящие вершины одного уровня, объединение которых дало отрезок, за который отвечает вершина предыдущего уровня), а всего уровней , то операция выполняется за .
Пример
Рассмотрим данный алгоритм на примере задачи (Range Sum Query — запрос суммы на отрезке).
При этом сумма на текущем полуинтервале (в случае вызова рекурсий от детей) равна сумме результатов выполнения операции на этих детях.
Пусть дерево содержит листьев и запрашиваемая сумма — это отрезок (полуинтервал ).
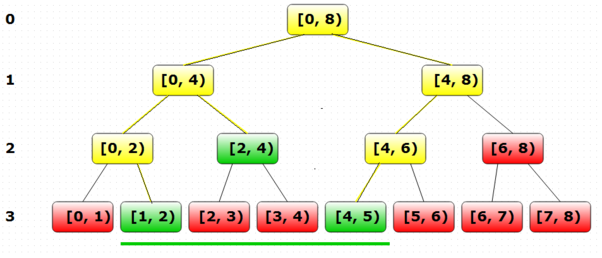
Рассмотрим данный алгоритм на определенных глубинах рекурсии, то есть на разных уровнях дерева (на рисунке глубина обозначена слева от уровня):
- На глубине .
- Текущий полуинтервал пересекается с рекурсивно переходим к и
- На глубине .
- и пересекаются с переходим по рекурсивным вызовам на полуинтервалах , , и
- На глубине .
- и пересекаются с переходим в листья
- полностью лежит внутри возвращаем сумму на этом отрезке
- не пересекается с возвращаем нулевое значение
- На глубине .
- Листья лежат в запрашиваемом интервале возвращаем значения в них
- Листья лежат вне возвращаем нейтральное значение
Таким образом ответ на полуинтервале равен сумме значений в вершинах, отвечающих за полуинтервалы , и .
Реализация
Рассмотрим реализацию задачи о дереве отрезков с произвольной ассоциативной бинарной операцией.
Пусть в узлах дерева хранятся структуры из трех полей:
- — левая граница полуинтервала, за который "отвечает" текущая вершина.
- — правая граница этого полуинтервала.
- — результат операции на полуинтервале.
int query(int node, int a, int b)
l = tree[node].left
r = tree[node].right
if [l, r) [a, b) ==
return // — нейтральный для данной операции элемент
if [l, r) [a, b)
return tree[node].res
return query(node * 2 + 1, a, b) query(node * 2 + 2, a, b)