Регуляризация
| Определение: |
| Регуляризация (англ. regularization) в статистике, машинном обучении, теории обратных задач — метод добавления некоторых дополнительных ограничений к условию с целью решить неккоректно поставленную задачу или предотвратить переобучение. Чаще всего эта информация имеет вид штрафа за сложность модели. |
Содержание
Мотивация
Как говорилось ранее, регуляризация полезна для борьбы с переобучением. Если вы выбрали сложную модель, и при этом у вас недостаточно данных, то легко можно получить итоговую модель, которая хорошо описывает обучающую выборку, но не обобщается на тестовую.
На примере линейной регрессии
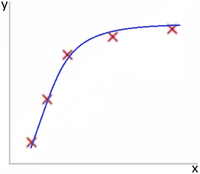
В качестве наглядного примера можно рассмотреть линейные регрессионные модели. Восстановить зависимость для нескольких точек можно пытаться полиномами разной степени M.
Как можно видеть на Рис 1. представлена зависимость, которая хорошо подходит для описания данных, а на Рис. 2 - модель слишком сильно заточилась под обучающую выборку.
Одним из способов бороться с этим эффектом - использовать регуляризацию, т. е. добавлять некоторый штраф за большие значения коэффициентов у линейной модели. Тем самым мы запретим слишком "резкие" изгибы и ограничим возможность подстраивания модели под данные.
На примере логистической регрессии
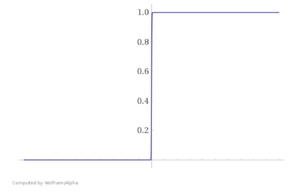
Необходимость регуляризации можно увидеть и на другом примере. Представьте, что ваша обучающая выборка была линейно разделима. В таком случае в процессе оптимизации значения весов уйдут в бесконечность и вместо сигмойды получится "ступенька", как представлено на Рис. 3.
Это плохо, ибо мы переобучились на нашу обучающую выборку. Как и в предыдущем примере, побороться с этим можно путем добавлением регуляризации, не дающей весам принимать слишком большие значения.
Основные виды регуляризации
Переобучение в большинстве случаев проявляется в том, что итоговые модели имеют слишком большие значения параметров. Соответственно, необходимо добавить в целевую функцию штраф за это. Наиболее часто используемые виды регуляризации - и , а также их линейная комбинация - эластичная сеть.
В представленных ниже формулах для эмпирического риска : является функцией потерь, а - вектором параметров элемента модели алгоритмов.
-регуляризация
| Определение: |
-регуляризация, или регуляризация Тихонова (англ. ridge regularization или Tikhonov regularization):
|
Минимизация регуляризованного cоответствующим образом эмпирического риска приводит в данном случае к выбору такого вектора параметров , которое не слишком сильно отклоняется от нуля. В линейных классификаторах это позволяет избежать проблем мультиколлинеарности и переобучения.
-регуляризация
| Определение: |
-регуляризация(англ. lasso regularization), или регуляризация через манхэттенское расстояние:
|
Данный вид регуляризации также позволяет ограничить значения вектора . Однако, он также обладает интересным и полезным на практике свойством - обнуляет значения некоторых параметров, что в случае с линейными моделями приводит к отбору признаков.
Запишем задачу настройки вектора параметров :
- ,
где - некоторая ограниченная гладкая функция потерь. Сделаем замену переменных, чтобы функционал стал гладким. Каждой переменной поставим в соответствие две новые неотрицательные переменные:
Тогда:
В новых переменных функционал становится гладким, но добавляется ограничения-неравенства:
Для любого хотя бы одно из ограничений и обращается в равенство, иначе второе слагаемое в можно было бы уменьшить, не изменив первое. Если гиперпараметр устремить к , в какой-то момент ограничений обратятся в равенство. Постепенное увеличение гиперпараметра приводит к увеличению числа таких , для которых , откуда следует, что . Как говорилось ранее, в линейных моделях это означает, что значения -го признака игнорируются, и его можно исключить из модели.
Эластичная сеть
| Определение: |
Эластичная сеть (англ. elastic net regularization):
|
Приведенная регуляризация использует как , так и регуляризации, учитывая эффективность обоих методов. Ее полезной особенностью является то, что она создает условия для группового эффекта при высокой корреляции переменных, а не обнуляет некоторые из них, как в случае с -регуляризацией.
Вероятностная интерпретация регуляризации
Эквивалентная вероятностная задача
Перед нами стоит задача - минимизировать эмпирический риск:
Вероятностная модель данных дает возможность по-другому взглянуть на задачу. Пусть - является вероятностным пространством. Тогда вместо задана совместная плотность распределение объектов и классов .
Для настройки вектора параметров \beta воспользуемся принципом максимума правдоподобия:
Удобнее рассматривать логарифм правдоподобия:
Можно заключить, что задачи в исходном и вероятностном представлении эквивалентны, если положить:
Принцип максимума совместного правдоподобия данных и модели
Допустим, что наряду с параметрической моделью плотности распределения имеется еще и априорное распределение в пространстве параметров модели . Чтобы ослабить априорные ограничения, вместо фиксированной функции вводится параметрическое семейство априорных распределений , где - гиперпараметр.
Принцип максимума правдоподобия теперь будет записываться по-другому, так как не только появление выборки , но и появление модели также является случайным. Их совместное появление описывается, согласно формуле условной вероятности, плотностью распределения:
Таким образом, приходим к принципу максимума совместного правдоподобия данных и модели:
Функционал распадается на два слагаемых: логарифм правдоподобия и регуляризатор, не зависящий от данных. Второе слагаемое ограничивает вектор параметров модели, не позволяя ему быть каким угодно.
В итоге мы получили, что с байесовской точки зрения многие методы регуляризации соответствуют добавлению некоторых априорных распределений на параметры модели. При этом можно определить распределения, которые соответствуют представленным ранее и регуляризаторам.
Нормальный регуляризатор
Пусть вектор имеет нормальное распределение, все его компоненты независимы и имеют равные дисперсии:
Логарифмируя, получаем квадратичный регуляризатор:
где - слагаемое, не зависящее от , которым можно пренебречь, поскольку оно не влияет на решение оптимизационной задачи. В итоге имеем - регуляризатор.
Лапласовский регуляризатор
Пусть вектор имеет распределение Лапласа, все его компоненты независимы и имеют равные дисперсии:
Тогда:
Распределение Лапласа имеет более острый пик и более тяжёлые «хвосты», по сравнению с нормальным распределением. Его дисперсия равна .
Аналогично случаю с нормальным регуляризатором, можно опустить и, таким образом, получаем - регуляризатор.
Регуляризация в линейной регрессии
Гребневая регрессия
Лассо регрессия
Сравнение гребниевой и лассо регрессий
Байесовская регрессия
Регуляризация в алгоритмах
Гррадиентный спуск
Алгоритм градиентного спуска используют для нахождения аппроксимирующей зависимости, находя вектор весов , при котором достигается минимум эмпирического риска:
В этом методевыбирается некоторое начальное приближение для вектора весов , затем запускается итерационный процесс, на каждом шаге которого вектор w изменяется в направлении наиболее быстрого убывания функционала Q - противоположно вектору градиента :
- ,
где - величина шага в направлении антиградиента.
Регуляризация - одна из эвристик улучшения градиентных методов обучения. Основным способом уменьшить переобучение является квадратичная регуляризация, называемая также сокращением весов. Чтобы ограничить рост абсолютных значений весов, к минимизируемому функционалу добавляется штрафное слагаемое:
Это приводит к появлению аддитивной поправки в градиенте:
В результате правило обновления весов принимает вид:
Таким образом, вся модификация сводится к появлению неотрицательного множителя , приводящего к постоянному уменьшению весов.
Достоинства
- Предотвращается паралич,
- повышается устойчивость весов в случае мультиколлинеарности,
- повышается обобщающая способность алгоритма и снижается риск переобучения.
Недостатки
- Параметр необходимо выбирать с помощью кросс-валидации, что связано с большими вычислительными затратами.
Метод опорных векторов
Метод опорных векторов используется для задачи бинарной классификации. В нем строится гиперплоскость, разделяющая множества разных классов.
К сожалению, зачастую выборка является линейно неразделимой. В таком случае приходится "ослаблять ограничения", позволяя некоторым объектам попадать на территорию другого класса. Для каждого объекта от отступа отнимается некоторая положительная величина $\xi_i$, но требуется, чтобы введенные поправки были минимальны. В итоге постановка задачи SVM с мягким отступом (англ. soft-margin SVM) выглядит следующим образом: $\begin{cases} \frac{1}{2} \lVert w \rVert^2 + C \sum\limits_{i=1}^\ell \xi_i \to \min\limits_{w, b, \xi} \\ M_i(w, b) \geq 1 - \xi_i, \quad i = 1, \ldots, \ell \\ \xi_i \geq 0, \quad i = 1, \ldots, \ell \\ \end{cases}$
Как показано в соответствующем данному алгоритму разделе, эквивалентной задачей безусловной минимизации является: $Q(w, b) = \frac{1}{2C} \lVert w \rVert^2 + \sum\limits_{i=1}^\ell \left(1 - M_i(w, b)\right)_+ \to \min\limits_{w, b}$
В силу неравенства $[M_{i} < 0] \leq (1 - M_{i})_{+}$, функционал $Q(w, b)$ как верхнюю оценку эмпирического риска, к которому добавлен регуляризатор $\frac{1}{2C} \|\w|\|2$.
С введением регуляризатора устраняется проблема мультиколлинеарности, повышается устойчивость алгоритма, улучшается его обобщающая способность.
В результате получаем, что принцип оптимальной разделяющей гиперплоскости или максимизации ширины разделяющей полосы в случае неразделимой выборки тесно связан с $L_{2}$-регуляризацией, которая возникает естественным образом из постановки задачи.