Реляционная алгебра: унарные операции
В этом разделе будут описаны унарные операции в рамках реляционной алгебры. В соответствии с определением, для определения каждой операции нужно указать способ построения заголовка, тела отношения, а также условия применимости, если такие есть.
Проекция
| Определение: |
| — проекция отношения на аттрибуты . Заголовок результирующего отношения: пересечение заголовка с . |
Данная операция полезна как минимум для следующего:
- Привести отношение к виду, в котором с ним можно будет осуществить другую операцию (например, объединение);
- Выбрать из отношения только нужные данные (для выборки).
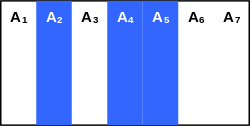
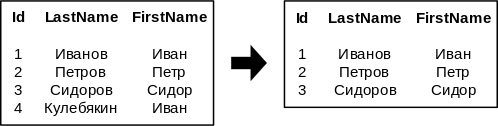
Ниже приведено пояснение определения для операции :
Синим обозначены столбцы, которые есть в результирующем отношении. Остальные столбцы не используются, и результат не зависит от данных, которые там находятся.
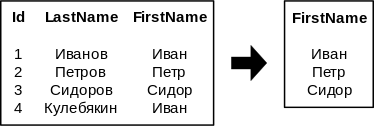
Примеры
Приведем несколько тривиальных примеров применения проекции.
Фильтрация
| Определение: |
| — фильтрация (селекция, выборка из) отношения по условию. Заголовок результирующего отношения равен заголовку исходного. |
Данная операция крайне часто используется для
- Ограничения области действия изменяющих запросов;
- Получения выборки данных, соответствующих определенному условию.
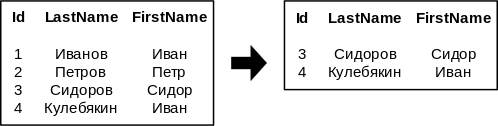
Примеры
Приведем несколько тривиальных примеров применения фильтрации.
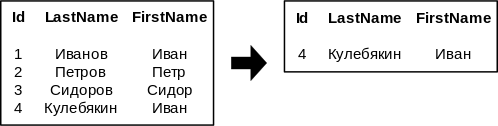
- Можно писать и более сложные условия:
- Еще можно исопльзовать функции, доступные в БД:
Стоит обратить внимание на то, что отношение — это множество, поэтому повторяющиеся кортежи учитываются ровно по одному разу.
Переименование
| Определение: |
| — изменение имени атрибута. Заголовок результирующего отношения равен заголовку исходного с точностью до изменения названий на . |
Операция часто применяется для того, чтобы отношение можно было использовать в рамках другой операции (например, при объединении с другим отношением).
Примеры
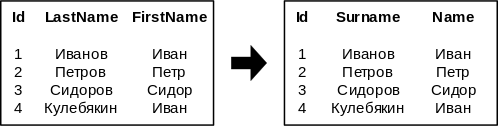
Ниже приведен тривиальный пример-пояснение для операции переименования.