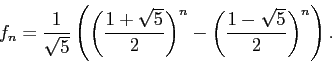Решение рекуррентных соотношений — различия между версиями
| Строка 28: | Строка 28: | ||
==Примеры== | ==Примеры== | ||
====ЧИСЛА ФИБОНАЧЧИ==== | ====ЧИСЛА ФИБОНАЧЧИ==== | ||
| − | |||
| − | |||
Рассмотрим рекуррентное соотношение для чисел Фибоначчи: | Рассмотрим рекуррентное соотношение для чисел Фибоначчи: | ||
<br>[[Файл:Img39.png]]<br> | <br>[[Файл:Img39.png]]<br> | ||
| − | |||
Это хорошо известная последовательность, каждый элемент которой (кроме нулевого и первого) равен сумме двух предыдущих: | Это хорошо известная последовательность, каждый элемент которой (кроме нулевого и первого) равен сумме двух предыдущих: | ||
<br>[[Файл:Img40.png]]<br> | <br>[[Файл:Img40.png]]<br> | ||
| − | |||
| − | |||
Первый шаг алгоритма мы уже выполнили, записав рекуррентное соотношение. Выполним второй шаг: | Первый шаг алгоритма мы уже выполнили, записав рекуррентное соотношение. Выполним второй шаг: | ||
<br>[[Файл:Img45.png]]<br> | <br>[[Файл:Img45.png]]<br> | ||
| Строка 45: | Строка 40: | ||
откуда получаем замкнутое выражение для производящей функции: | откуда получаем замкнутое выражение для производящей функции: | ||
<br>[[Файл:Img48.png]]<br> | <br>[[Файл:Img48.png]]<br> | ||
| − | Осталось | + | Осталось разложить её в ряд (чего требует четвёртый шаг алгоритма). С этой целью нужно разложить знаменатель на множители. Найдем корни уравнения: |
<br>[[Файл:Img49.png]]<br> | <br>[[Файл:Img49.png]]<br> | ||
| − | Таким образом | + | Таким образом, |
<br>[[Файл:Img50.png]]<br> | <br>[[Файл:Img50.png]]<br> | ||
| − | + | Нам известно разложение только следующей рациональной функции: | |
<br>[[Файл:Img31.png]]<br> | <br>[[Файл:Img31.png]]<br> | ||
| − | Рассмотрим первую дробь и поделим в ней числитель и знаменатель на z1: | + | Рассмотрим первую дробь и поделим в ней числитель и знаменатель на <math>z1</math>: |
<br>[[Файл:Img52.png]]<br> | <br>[[Файл:Img52.png]]<br> | ||
| − | Аналогично (но с делением на z2) поступим со второй дробью: | + | Аналогично (но с делением на <math>z2</math>) поступим со второй дробью: |
<br>[[Файл:Img53.png]]<br> | <br>[[Файл:Img53.png]]<br> | ||
Таким образом, | Таким образом, | ||
| Строка 59: | Строка 54: | ||
и, следовательно, | и, следовательно, | ||
<br>[[Файл:Img55.png]]<br> | <br>[[Файл:Img55.png]]<br> | ||
| − | Данное выражение можно | + | Данное выражение можно упростить, если обратить внимание на то, что <math>1/z1=-z2</math>, <math>1/z2=-z1</math> и <math>z1-z2=√5</math>: |
<br>[[Файл:Img59.png]]<br> | <br>[[Файл:Img59.png]]<br> | ||
| + | |||
====БОЛЕЕ СЛОЖНОЕ СООТНОШЕНИЕ==== | ====БОЛЕЕ СЛОЖНОЕ СООТНОШЕНИЕ==== | ||
Версия 22:13, 12 марта 2018
Содержание
Определения
| Определение: |
| Рекуррентная формула — формула вида , выражающая каждый член последовательности через предыдущих членов и возможно номер члена последовательности . |
Во многих задачах полезно знать, есть ли у рекурсивной функции нерекурсивная или как еще говорят «замкнутая» форма, т.е. получение в виде аналитически заданной функции. Например, рекурсивная функция, описывающая сумму чисел натурального ряда:
может быть переведена в замкнутую форму: . Для этого можно использовать метод производящих функций.
Метод производящих функций
Алгоритм получения замкнутого выражения для чисел , удовлетворяющих рекуррентному соотношению, с помощью производящих функций cостоит из 4 шагов.
- Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен ):

- Домножить каждую строчку на в соответствующей степени и просуммировать строчки для всех .
- В полученном уравнениипривести все суммы к замкнутому виду. Получить уравнение для производящей функции.
- Выразить в явном виде (решить уравнение, полученное на предыдущем шаге) и разложить производящую функцию в ряд по степеням .
Доказательство
по построению
Примеры
ЧИСЛА ФИБОНАЧЧИ
Рассмотрим рекуррентное соотношение для чисел Фибоначчи:
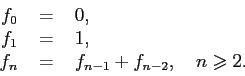
Это хорошо известная последовательность, каждый элемент которой (кроме нулевого и первого) равен сумме двух предыдущих:

Первый шаг алгоритма мы уже выполнили, записав рекуррентное соотношение. Выполним второй шаг:
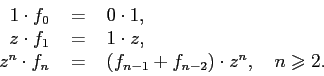
Складываем все строчки:
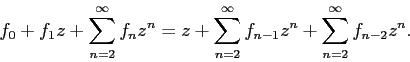
Третий шаг алгоритма требует привести все суммы к замкнутому виду:
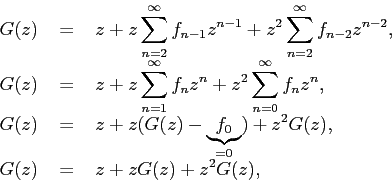
откуда получаем замкнутое выражение для производящей функции:
![]()
Осталось разложить её в ряд (чего требует четвёртый шаг алгоритма). С этой целью нужно разложить знаменатель на множители. Найдем корни уравнения:
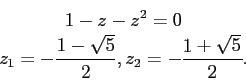
Таким образом,
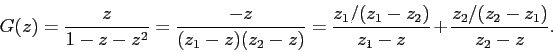
Нам известно разложение только следующей рациональной функции:
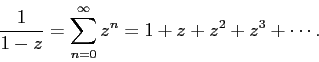
Рассмотрим первую дробь и поделим в ней числитель и знаменатель на :
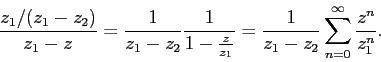
Аналогично (но с делением на ) поступим со второй дробью:
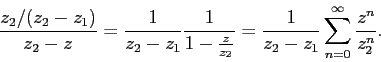
Таким образом,
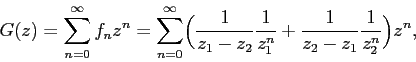
и, следовательно,
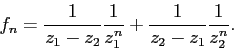
Данное выражение можно упростить, если обратить внимание на то, что , и :