Связь между максимизацией гиперобъема и аппроксимацией Парето-фронта — различия между версиями
м (→Индикатор гиперобъема) |
м (→Индикатор гиперобъема) |
||
| Строка 35: | Строка 35: | ||
|statement=Пусть <tex>f \in \mathbb{F}, n \in \mathbb{N}</tex>. | |statement=Пусть <tex>f \in \mathbb{F}, n \in \mathbb{N}</tex>. | ||
Тогда существует, не обязятельно единственное, множество-решение <tex>X \in \mathbb{X}</tex>, которое максимизирует значение [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Индикатор Гиперобъема|гиперобъема]] <tex>HYP(X)</tex> на <tex>\mathbb{X}</tex> | Тогда существует, не обязятельно единственное, множество-решение <tex>X \in \mathbb{X}</tex>, которое максимизирует значение [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Индикатор Гиперобъема|гиперобъема]] <tex>HYP(X)</tex> на <tex>\mathbb{X}</tex> | ||
| − | + | }} | |
Доказательство представлено в статье [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Индикатор Гиперобъема|Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем]] | Доказательство представлено в статье [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Индикатор Гиперобъема|Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем]] | ||
| − | |||
==Нахождение лучшего коэффициента аппроксимации== | ==Нахождение лучшего коэффициента аппроксимации== | ||
Версия 00:30, 20 июня 2012
Содержание
Основные определения
| Определение: |
| Множество функций вида: , где убывает и обозначим через . |
Коэффициент апроксимации монотонно убывающих функций не зависит от масштабов отрезков и . Так как для фиксированных констант функция и имеет тот же коэффициент аппроксимации. Однако, коэффициент аппроксимации зависит от значений и .
| Определение: |
| Фиксируем . Для фиксированного отрезка будем называть кортеж , такой что — множеством-решением. Множество таких решений будем обозначать . |
| Определение: |
| Пусть и . Тогда вкладом -й точки в гиперобъем решения называется
. Минимальным вкладом в гиперобъем множества-решения называется . |
Далее будем рассматривать только монотонно убывающие, полунепрерывные Парето-фронты. Условие полунепрерывности необходимо для того, чтобы существовало множество-решение, максимизирующее индикатор гиперобъема.
Рассмотрим оптимальный коэффициент апроксимации для данного Парето-фронта из точек и верхнюю границу коэффициента аппроксимации для множества из точек, максимизирующего значение индикатора гиперобъема , и докажем, что для количества точек они одинаковы, а именно равны .
Индикатор гиперобъема
| Утверждение (1): |
Пусть .
Тогда существует, не обязятельно единственное, множество-решение , которое максимизирует значение гиперобъема на |
Доказательство представлено в статье Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем
Нахождение лучшего коэффициента аппроксимации
Утверждение(3) ограничивает значение оптимального коэффицента апроксимации сверху: = .
Нахождение коэффициента аппроксимации множества решения максимизируюшего гиперобъем
| Утверждение (2): |
Пусть и .
Тогда минимальный вклад данного множества-решения: |
|
Исходя из определения минимальный вклад в гиперобъем множества равен минимуму из всевозможных площадей прямоугольников, образующихся между соседними точками множества-решения и их значениями. Пусть — длины сторон соответствующего прямоугольника, тогда:
Это означает:
и поэтому: Так как среднее гармоническое не больше среднего арифметического: |
Далее необходимо посчитать коэффициент аппроксимации для "внутренних" () и "внешних" точек ( или ).
| Теорема (1): |
Пусть . Любое множество-решение достигает аппроксимации всех внутренних точек. |
| Доказательство: |
|
Допустим, что существует , который не аппроксимируется . Пусть , тогда . Известно, что . После подстановки получим (1). Применив утверждение(2), получим: (2) (3) Таким образом, . Т.к. монотонно убывает, а монотонно возрастает, то максимальное значение достигается при равенстве обоих членов: . Получим верхнюю оценку для : . Вышесказанное верно для . Для из (1) и (3) следует, что , что невозможно по условию теоремы. Для по (1) и (2) , что тоже невозможно по условию теоремы. |
| Теорема (2): |
Пусть . И является точкой отсчета. Каждое множество решение достигает аппроксимации всех точек с и аппроксимации всех точек с . |
| Доказательство: |
| Доказательство производится c использованием ранее доказанного утверждения о . |
Из теоремы(1) и теоремы(2) выводятся следующие следствия:
Следствие 1:
Пусть , и является точкой отсчета. Тогда:
Следствие 2:
Пусть . И является точкой отсчета. Тогда если
или
, выполняется следующее неравенство
= ,
то есть
= ,
что и требовалось доказать.
Примечание
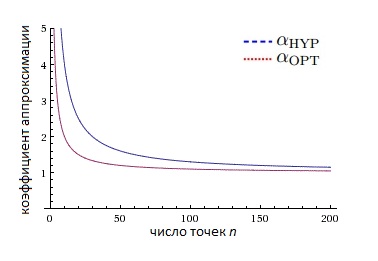
Конечно, зависимость от и в аппроксимационном коэффициенте оптимального множества решения меньше чем в аппроксимационном коэффициенте для множества, максимизирующего гиперобъем. Однако, полученная граница для коэффициента аппроксимации является верхней. На рисунке ниже можно увидеть пример поведения данных значений для определенного класса функций.