Связь между максимизацией гиперобъема и аппроксимацией Парето-фронта — различия между версиями
(→Свзяь между максимизацией гиперобъема и аппроксимацией Парето-фронта) |
|||
| Строка 8: | Строка 8: | ||
}} | }} | ||
| − | + | Множество функций вида: <tex>f:[a,A] \rightarrow [b,B]</tex>, где <tex>f</tex> убывает и <tex>f(a)=B, f(A)=b</tex> обозначим через <tex>\mathbb{F}</tex>. | |
{{Определение | {{Определение | ||
| − | |definition= | + | |definition=Оптимальный коэффицент аппроксимации <tex>\alpha_{opt} = \sup \limits_{f \in \mathbb{F}} \inf \limits_{x \in \mathbb{X}} \alpha (f, X)</tex> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Оптимальный коэффицент аппроксимации <tex>\alpha_{opt} = \sup \limits_{f \in \mathbb{F}} \inf \limits_{x \in \mathbb{X}} \alpha (f, X)</tex> | ||
}} | }} | ||
=Свзяь между максимизацией гиперобъема и аппроксимацией Парето-фронта= | =Свзяь между максимизацией гиперобъема и аппроксимацией Парето-фронта= | ||
| − | Коэффициент апроксимации монотонно убывающих функций не зависит от масштабов отрезков <tex> [a,A]</tex> и <tex>[b,B] </tex>. Так как для фиксированных констант <tex> \mu , \nu </tex> функция <tex> f^*:[ \mu a , \mu A ] \rightarrow [ \nu b , \nu B ]</tex> и <tex> f^*= \nu f(x/ \mu ) </tex> имеет тот же коэффициент аппроксимации. Однако, коэффициент аппроксимации зависит от значений <tex>A/a</tex> и <tex>B/b</tex>. | + | [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Коэффициент апроксимации|Коэффициент апроксимации]] монотонно убывающих функций не зависит от масштабов отрезков <tex> [a,A]</tex> и <tex>[b,B] </tex>. Так как для фиксированных констант <tex> \mu , \nu </tex> функция <tex> f^*:[ \mu a , \mu A ] \rightarrow [ \nu b , \nu B ]</tex> и <tex> f^*= \nu f(x/ \mu ) </tex> имеет тот же коэффициент аппроксимации. Однако, коэффициент аппроксимации зависит от значений <tex>A/a</tex> и <tex>B/b</tex>. |
Далее будем рассматривать только монотонно убывающие, полунепрерывные Парето-фронты. Условие полунепрерывности необходимо для того, [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Индикатор Гиперобъема|чтобы существовало множество решение, максимизирующее индикатор гиперобъема]]. | Далее будем рассматривать только монотонно убывающие, полунепрерывные Парето-фронты. Условие полунепрерывности необходимо для того, [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Индикатор Гиперобъема|чтобы существовало множество решение, максимизирующее индикатор гиперобъема]]. | ||
| Строка 35: | Строка 29: | ||
{{Утверждение | {{Утверждение | ||
|statement=Пусть <tex>f \in \mathbb{F}, n \in \mathbb{N}</tex>. | |statement=Пусть <tex>f \in \mathbb{F}, n \in \mathbb{N}</tex>. | ||
| − | Тогда существует, не обязятельно единственное, множество решения <tex>X \in \mathbb{X}</tex>, которое максимизирует значение <tex>HYP(X)</tex> на <tex>\mathbb{X}</tex> | + | Тогда существует, не обязятельно единственное, множество решения <tex>X \in \mathbb{X}</tex>, которое максимизирует значение [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Индикатор Гиперобъема|<tex>HYP(X)</tex>]] на <tex>\mathbb{X}</tex> |
|proof= | |proof= | ||
См. [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Индикатор Гиперобъема|статью Гиперобъем]] | См. [[Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем#Индикатор Гиперобъема|статью Гиперобъем]] | ||
| Строка 115: | Строка 109: | ||
что и требовалось доказать. | что и требовалось доказать. | ||
| + | |||
| + | {{Определение | ||
| + | |id=definition6 | ||
| + | |about=6 | ||
| + | |definition=Пусть <tex>f \in \mathbb{F}, n \geq 3</tex> и <tex>X = \{x_1, \ldots, x_n\} \in \mathbb{X}</tex>. Наименьшим вкладом этого множества называется <tex>MinCon(X)= \min \limits_{2 \leq i \leq n-1} (x_i-x_{i-1})(f(x_i)- f(x_{i-1}))</tex>. | ||
| + | }} | ||
| + | |||
| + | {{Утверждение | ||
| + | |id=statement5 | ||
| + | |about=5 | ||
| + | |statement=Пусть <tex>f \in \mathbb{F}, n \geq 3</tex> и <tex>X = \{x_1, \ldots, x_n\} \in \mathbb{X}</tex>, тогда | ||
| + | <tex>MinCon(X) \leq \frac{(x_n-x_1)(f(x_1)-f(x_n))}{(n-2)^2}</tex>. | ||
| + | |proof= | ||
| + | Пусть <tex>a_i=x_i-x_{i-1}</tex> <tex>\forall i \in [2,n]</tex> и <tex>b_i=f(x_i)-f(x_{i-1})</tex> <tex>\forall i \in [1,n-1]</tex>. | ||
| + | Подставив в [[#definition6|определение(6)]], получим: | ||
| + | |||
| + | <tex>MinCon(X)= \min \limits_{2 \leq i \leq n-1} a_i b_i \Leftrightarrow a_i \geq MinCon(X) / b_i \forall i \in [2, n-1]</tex> | ||
| + | |||
| + | <tex>\sum \limits_{i=2}^{n-1} MinCon(X) / b_i \leq \sum \limits_{i=2}^{n-1} a_i \leq \sum \limits_{i=2}^{n} a_i = \sum \limits_{i=2}^{n}x_i - \sum \limits_{i=1}^{n-1}x_i=x_n-x_1 </tex> | ||
| + | |||
| + | Тогда <tex>MinCon(X) \leq \frac{x_n-x_1}{\sum \limits_{i=2}^{n-1}1/b_i}</tex>. | ||
| + | |||
| + | Cреднее гармоническое меньше среднего арифметического, поэтому | ||
| + | <tex>MinCon(X) \leq \frac{x_n-x_1}{\sum \limits_{i=2}^{n-1}1/b_i} \leq \frac{(x_n-x_1)\sum \limits_{i=2}^{n-1}b_i}{(n-2)^2} \leq \frac{(x_n-x_1)(f(x_1)-f(x_n))}{(n-2)^2}</tex>. | ||
| + | }} | ||
| + | |||
| + | {{Теорема | ||
| + | |statement=Пусть <tex>f \in \mathbb{F}, n > 4</tex> и <tex>X = \{ x_1, \ldots, x_n \} \in \mathbb{X}</tex>. Тогда | ||
| + | <tex>\alpha = 1 + \frac{\sqrt{A/a} + \sqrt{B/b}}{n-4}</tex>. | ||
| + | |proof= | ||
| + | Допустим, что существует <tex>x</tex>, который не аппроксимируется <tex>\alpha = 1 + \frac{\sqrt{A/a} + \sqrt{B/b}}{n-4}</tex>. | ||
| + | Пусть <tex>x_i < x < x_i+1</tex>, тогда <tex>x > \alpha x_i, f(x) > \alpha f(x_{i+1})</tex>. | ||
| + | |||
| + | Известно, что <tex>MinCon(X) \geq (x-x_i)(f(x)-f(x_{i+1}))</tex>. | ||
| + | |||
| + | После подстановки получим <tex>MinCon(X) > (\alpha - 1)^2 x_i f(x_{i+1})</tex> (1). | ||
| + | |||
| + | Применив [[#statement5|утверждение(5)]], получим: | ||
| + | |||
| + | <tex>\forall i \in [3, n-1]</tex> <tex>MinCon(X) \leq (x_i-x_1)(f(x_1)-f(x_i))/(i-2)^2 \leq x_iB/(i-2)^2</tex> (2) | ||
| + | |||
| + | <tex>\forall i \in [1, n-3]</tex> <tex>MinCon(X) \leq (x_n-x_{i+1})(f(x_{i+1})-f(x_n))/(n-i-2)^2 \leq A f(x_{i+1})/(n-i-2)^2</tex> (3) | ||
| + | |||
| + | Таким образом, <tex>(\alpha - 1)^2 x_i f(x_{i+1}) < \min \{\frac{x_iB}{(i-2)^2} ,\frac{A f(x_{i+1})}{(n-i-2)^2}\} \Leftrightarrow</tex> <tex>\alpha < 1 + \min \{\frac{\sqrt{x_iB}}{i-2} ,\frac{\sqrt{A f(x_{i+1})}}{n-i-2}\}</tex>. | ||
| + | |||
| + | Т.к. <tex>\frac{\sqrt{x_iB}}{i-2}</tex> монотонно убывает, а <tex>\frac{\sqrt{A f(x_{i+1})}}{n-i-2}\}</tex> монотонно возрастает, то максимальное значение <tex>\min \{\frac{\sqrt{x_iB}}{i-2} ,\frac{\sqrt{A f(x_{i+1})}}{n-i-2}\}</tex> достигается при равенстве обоих членов: | ||
| + | |||
| + | <tex>\frac{\sqrt{x_iB}}{i-2} = \frac{\sqrt{A f(x_{i+1})}}{n-i-2}\} \Leftrightarrow i = 2 + \frac{(n-4)\sqrt{B/b}}{\sqrt{A/a} + \sqrt{B/b}}</tex>. | ||
| + | |||
| + | Получим верхнюю оценку для <tex>\alpha</tex>: <tex>\alpha < 1 + \frac{\sqrt{A/a} + \sqrt{B/b}}{n-4}</tex>. | ||
| + | |||
| + | Вышесказанное верно для <tex>3 \leq i \leq n-3</tex>. | ||
| + | |||
| + | Для <tex>i = 1, 2</tex> из (1) и (3) следует, что <tex>\alpha < 1 + \frac{\sqrt{A/a}}{n-i-2} \leq 1 + \frac{\sqrt{A/a}}{n-4}</tex>, что невозможно по условию теоремы. | ||
| + | |||
| + | Для <tex>i = n-2, n-1</tex> по (1) и (2) <tex>\alpha < 1 + \frac{ \sqrt{B/b} } {i-2} \leq 1 + \frac {\sqrt {B/b} } {n-4}</tex>, что тоже невозможно по условию теоремы. | ||
| + | |||
| + | }} | ||
=Примечание= | =Примечание= | ||
Версия 19:03, 19 июня 2012
Содержание
Основные определения
| Определение: |
| Множество называется Парето оптимальным, если:
, где ( доминирует ) - множество оптимальных по Парето решений, его также называют Парето-фронтом. Парето-фронт не может быть вычислен за полиномиальное время. |
Множество функций вида: , где убывает и обозначим через .
| Определение: |
| Оптимальный коэффицент аппроксимации |
Свзяь между максимизацией гиперобъема и аппроксимацией Парето-фронта
Коэффициент апроксимации монотонно убывающих функций не зависит от масштабов отрезков и . Так как для фиксированных констант функция и имеет тот же коэффициент аппроксимации. Однако, коэффициент аппроксимации зависит от значений и .
Далее будем рассматривать только монотонно убывающие, полунепрерывные Парето-фронты. Условие полунепрерывности необходимо для того, чтобы существовало множество решение, максимизирующее индикатор гиперобъема.
Рассмотрим оптимальный коэффициент апроксимации для данного Парето-фронта из n () и верхнюю границу коэффициента аппроксимации для множества из n точек, максимизирующего значение индикатора гиперобъема () и докажем, что для количества точек они одинаковы, а именно .
Индикатор гиперобъема
| Определение: |
| Пусть дано множество решения . Пусть также множество всех решений усечено некоторой точкой . Тогда:
, где через обозначена мера множества по Лебегу. Гиперобъем является единственным унарным индикатором эластичным по Парето(Pareto-compliant). |
| Утверждение: |
| См. статью Гиперобъем |
Нахождение лучшего коэффициента аппроксимации
Доказательство ограничивает значение оптимального коэффицента апроксимации сверху: = .
Нахождение коэффициента аппроксимации множества решения максимизируюшего гиперобъем
| Утверждение: |
Пусть и .
Тогда [MINCON] данного множество решения: |
|
Исходя из определения минимальный вклад в гиперобъем множества равен минимуму из всевозможных площадей прямоугольников, образующихся между соседними точками множества решения и их значениями. Пусть - длины сторон соответствующего прямоугольника, тогда: , для любого Это означает:
и поэтому: Так как среднее гармоническое не больше среднего арифметического: Преобразуя, получаем искомое. |
Далее необходимо посчитать коэффициент аппроксимации для "внутренних" () и "внешних" точек ( или ).
| Теорема (1): |
Пусть . Любое множество решение достигает мультипликативной аппроксимации всех внутренних точек. |
| Доказательство: |
| Доказательство производится от противного, принимая предположение, что существует такой , для которого бы не выполнялось условие аппроксимации при данном коэффициенте. |
| Теорема (2): |
Пусть . И является точкой отсчета. Каждое множество решение достигает мультипликативной аппроксимации всех точек с , и достигает мультипликативной аппроксимации всех точек с . |
| Доказательство: |
| Доказательство производится c использованием ранее доказанного утверждения о MINCON. |
Совместно теорема(1) и теорема(2) приводят к следующим следствиям:
Следствие 1:
Пусть , и является точкой отсчета. Тогда:
Следствие 2:
Пусть . И является точкой отсчета. Тогда если
или
, выполняется следующее неравенство
= ,
то есть
= ,
что и требовалось доказать.
| Определение: |
| Пусть и . Наименьшим вкладом этого множества называется . |
| Утверждение (5): |
Пусть и , тогда
. |
|
Пусть и . Подставив в определение(6), получим:
Тогда . Cреднее гармоническое меньше среднего арифметического, поэтому . |
| Теорема: |
Пусть и . Тогда
. |
| Доказательство: |
|
Допустим, что существует , который не аппроксимируется . Пусть , тогда . Известно, что . После подстановки получим (1). Применив утверждение(5), получим: (2) (3) Таким образом, . Т.к. монотонно убывает, а монотонно возрастает, то максимальное значение достигается при равенстве обоих членов: . Получим верхнюю оценку для : . Вышесказанное верно для . Для из (1) и (3) следует, что , что невозможно по условию теоремы. Для по (1) и (2) , что тоже невозможно по условию теоремы. |
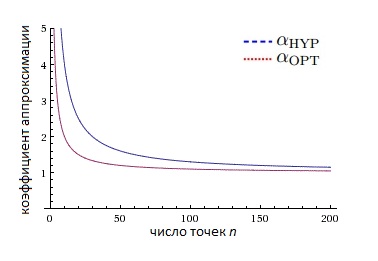
Примечание
Конечно, зависимость от и в аппроксимационном коэффициенте оптимального множества решения меньше чем в аппроксимационном коэффициенте для множества, максимизирующего гиперобъем. Однако, полученная граница для коэффициента аппроксимации является верхней. На рисунке ниже можно увидеть пример поведения данных значений для определенного класса функций.