Основные определения
| Определение: |
| Множество [math]X^* \subseteq X[/math] называется Парето оптимальным, если:
[math]\mathrm{\forall x^* \subset X^* \not \exists x \subset X : x \succ x^*}[/math],
где [math] x \succ x^* [/math]([math]x[/math] доминирует [math]x^*[/math])[math] \leftrightarrow \left( \forall i \in 1 \ldots d: f_i(x) \geq f_i(x^*) \right) \bigwedge \left( \exists i \in 1 \ldots d: f_i(x) \gt f_i(x^*)\right)[/math]
[math]P(X^*)[/math] - множество оптимальных по Парето решений, его также называют Парето-фронтом. Парето-фронт не может быть вычислен за полиномиальное время. |
| Определение: |
| Множество решений [math]\mathrm{X=\{x_1,x_2, \ldots , x_n\}}[/math] называется [math]\alpha[/math]-аппроксимацией функции [math]f \in \mathbb{F}[/math], если:
[math]\mathrm{\forall x \in [a,A] \exists x_i \in X : (x \leq \alpha x_i) \bigwedge (f(x) \leq \alpha f(x_i))}[/math]
Коэффицент аппроксимации функции [math]f[/math] на [math]X[/math] равен:
[math]\mathrm{\alpha (f, X) = inf \{\alpha | X} - \alpha[/math] аппроксимация [math]f \}[/math]
Оптимальный коэффицент аппроксимации [math]\alpha_{opt} = \sup \limits_{f \in \mathbb{F}} \inf \limits_{x \in \mathbb{X}} \alpha (f, X)[/math] |
Свзяь между максимизацией гиперобъема и аппроксимацией Парето-фронта
Рассмотрим функции вида: [math]f:[a,A] \rightarrow [b,B][/math], где [math]f[/math] убывает и [math]f(a)=B, f(A)=b[/math]. Коэффициент апроксимации монотонно убывающих функций не зависит от масштабов отрезков [math] [a,A][/math] и [math][b,B] [/math]. Так как для фиксированных констант [math] \mu , \nu [/math] функция [math] f^*:[ \mu a , \mu A ] \rightarrow [ \nu b , \nu B ][/math] и [math] f^*= \nu f(x/ \mu ) [/math] имеет тот же коэффициент аппроксимации. Однако, коэффициент аппроксимации зависит от значений [math]A/a[/math] и [math]B/b[/math].
Множество всех таких функций обозначим через [math]\mathbb{F}[/math]. Далее будем рассматривать только монотонно убывающие, полунепрерывные Парето-фронты. Условие полунепрерывности необходимо для того, чтобы существовало множество решение, максимизирующее индикатор гиперобъема.
Рассмотрим оптимальный коэффициент апроксимации для данного Парето-фронта из n ([math] \alpha _{OPT}[/math]) и верхнюю границу коэффициента аппроксимации для множества из n точек, максимизирующего значение индикатора гиперобъема ([math] \alpha _{HYP}[/math]) и докажем, что для количества точек [math] n [/math] они одинаковы, а именно [math] 1 + \Theta ( \frac{1}{n}) [/math].
Индикатор гиперобъема
| Определение: |
| Пусть дано множество решения [math]\mathrm{X \in \mathbb{R}^d}[/math]. Пусть также множество всех решений усечено некоторой точкой [math]\mathrm{r = \left(r_1, r_2, \ldots, r_d \right)}[/math]. Тогда:
[math]\mathrm{HYP\left(X\right)=VOL\left( \bigcup\limits_{\left(x_1, x_2, \ldots, x_d \right) \in X} \left[ r_1, x_1\right] \times \left[ r_2, x_2\right] \times \cdots \times \left[ r_d, x_d\right] \right)}[/math], где через [math]VOL(X)[/math] обозначена мера множества [math]X[/math] по Лебегу.
Гиперобъем является единственным унарным индикатором эластичным по Парето(Pareto-compliant). |
| Утверждение: |
Пусть [math]f \in \mathbb{F}, n \in \mathbb{N}[/math].
Тогда существует, не обязятельно единственное, множество решения [math]X \in \mathbb{X}[/math], которое максимизирует значение [math]HYP(X)[/math] на [math]\mathbb{X}[/math] |
| [math]\triangleright[/math] |
|
См. [Гиперобъем] |
| [math]\triangleleft[/math] |
Нахождение лучшего коэффициента аппроксимации
[Доказательство] ограничивает значение оптимального коэффицента апроксимации сверху: [math]1 + \frac{\log (\min ( \frac{A}{a}, \frac{B}{b}))}{n}[/math] = [math] 1 + \Theta ( \frac{1}{n}) [/math].
Нахождение коэффициента аппроксимации множества решения максимизируюшего гиперобъем
| Утверждение: |
Пусть [math]f \in \mathbb{F}, n \geq 3[/math] и [math]X= \{x_1, x_2, \ldots, x_d \} \in X [/math].
Тогда [MINCON] данного множество решения:
[math]MINCON(X) \leq \frac{(x_n - x_1)(f(x_1) - f(x_n))}{(n-2)^2}[/math] |
| [math]\triangleright[/math] |
|
Исходя из определения минимальный вклад в гиперобъем множества равен минимуму из всевозможных площадей прямоугольников, образующихся между соседними точками множества решения и их значениями.
Пусть [math]a_i, b_i[/math] - длины сторон соответствующего прямоугольника, тогда:
[math] a_i \geq MINCON(X)/b_i[/math], для любого [math]2 \leq i \leq n - 1[/math]
Это означает:
[math] \sum\limits_{i=2}^{n-1} MINCON(x)/b_i \leq \sum\limits_{i=2}^{n-1} a_i \leq \sum\limits_{i=2}^{n} a_i = \sum\limits_{i=2}^{n} x_i - \sum\limits_{i=1}^{n-1} x_i = x_n - x_1 [/math]
и поэтому:
[math]MINCON(X) \leq \frac{(x_n - x_1)}{\sum\limits_{i=2}^{n-1}1/b_i}[/math]
Так как среднее гармоническое не больше среднего арифметического:
[math] \frac{n - 2}{\sum\limits_{i=2}^{n-1}1/b_i} \leq \frac{\sum\limits_{i=2}^{n-1}1/b_i}{n - 2}[/math]
Преобразуя, получаем искомое. |
| [math]\triangleleft[/math] |
Далее необходимо посчитать коэффициент аппроксимации для "внутренних" ([math]x \in [x_1, x_n][/math]) и "внешних" точек ([math]x \lt x_1[/math] или [math]x \gt x_n[/math]).
| Теорема (1): |
Пусть [math]f \in \mathbb{F}, n \gt 4[/math]. Любое множество решение [math]\{x_1, x_2, \ldots, x_d\} \in X_{HYP}^f [/math] достигает [math]1 + \frac{ \sqrt{A/a} + \sqrt{B/b} }{n - 4}[/math] мультипликативной аппроксимации всех внутренних точек. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Доказательство производится от противного, принимая предположение, что существует такой [math] x[/math], для которого бы не выполнялось условие аппроксимации при данном коэффициенте. |
| [math]\triangleleft[/math] |
| Теорема (2): |
Пусть [math]f \in \mathbb{F}, n \gt 3[/math]. И [math] R = (R_x, R_y) \leq (0, 0) [/math] является точкой отсчета. Каждое множество решение [math]\{x_1, x_2, \ldots, x_d\} \in X_{HYP}^f [/math] достигает [math]1 + \frac{A}{(a - R_x)(n - 2)^2}[/math] мультипликативной аппроксимации всех точек с [math]x \lt x_1[/math], и достигает [math]1 + \frac{B}{(b - R_y)(n - 2)^2}[/math] мультипликативной аппроксимации всех точек с [math]x \gt x_n[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Доказательство производится c использованием ранее доказанного утверждения о MINCON. |
| [math]\triangleleft[/math] |
Совместно теоремы 1 и 2 приводят к следующим следствиям:
Следствие: [math]\alpha_{opt} = 1 + \Theta(1/n)[/math]
Пусть [math]f \in \mathbb{F}, n \gt 4[/math], и [math] R = (R_x, R_y) \leq (0, 0) [/math] является точкой отсчета. Тогда:
[math] \lambda_{HYP} \leq 1 + \max{ \frac{ \sqrt{A/a} + \sqrt{B/b} }{n - 4}}{\frac{A}{(a - R_x)(n - 2)^2}}{\frac{B}{(b - R_y)(n - 2)^2}}[/math]
Следствие: [math]\alpha_{opt} = 1 + \Theta(1/n)[/math]
Пусть [math]f \in \mathbb{F}, n \gt 4[/math]. И [math] R = (R_x, R_y) \leq (0, 0) [/math] является точкой отсчета. Тогда если
[math] n \geq 2 + \max{\sqrt{A/a}}{\sqrt{B/b}}[/math]
или
[math]R_x \leq - \sqrt{Aa}/n, R_y \leq - \sqrt{Bb}/n[/math],
выполняется следующее неравенство
[math] \alpha _{HYP} \leq 1 + \frac{ \sqrt{ \frac{A}{a}} + \sqrt{ \frac{B}{b}}}{n - 4}[/math] = [math] 1 + \Theta ( \frac{1}{n}) [/math],
то есть
[math] \alpha _{HYP} [/math] = [math] 1 + \Theta ( \frac{1}{n}) [/math],
что и требовалось доказать.
Примечание
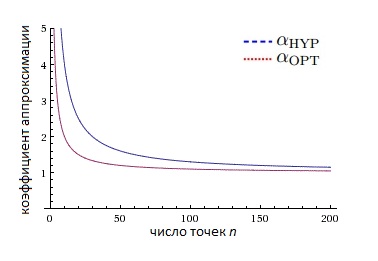
Конечно, зависимость от [math] [a,A][/math] и [math][b,B] [/math] в аппроксимационном коэффициенте оптимального множества решения меньше чем в аппроксимационном коэффициенте для множества, максимизирующего гиперобъем. Однако, полученная граница для коэффициента аппроксимации является верхней. На рисунке ниже можно увидеть пример поведения данных значений для определенного класса функций.
Источники
- Friedrich T., Bringmann K. - The Maximum Hypervolume Set Yields Near-optimal Approximation
