Сортирующие сети для квадратичных сортировок — различия между версиями

Материал из Викиконспекты
Перейти к: навигация, поиск
Строка 16: Строка 16:
 
=== Сортировка пузырьком и вставками ===
 
=== Сортировка пузырьком и вставками ===
  
−
* Если сжать последовательные сортирующие сети пузырьком и вставками, то результат будет одним и тем же.
+
Заметим, если сжать последовательные сортирующие сети пузырьком и вставками, то результат будет одним и тем же. Этот факт легко заметить, если сопоставлять компараторы на уровне <tex> k </tex> компараторам на уровне <tex> k - 2</tex>, где (<tex> k </tex> — уровень между <tex> k - 1 </tex> и <tex> k </tex> входом). Тем самым получаем картинку сводящуюся к "треугольнику".
  
 
{{
 
{{
 
Теорема
 
Теорема
 
|statement=
 
|statement=
−
  В результирующей сети будет <tex>(2n - 3)</tex> слоев.
+
  В результирующей сети будет <tex>(2n - 3)</tex> слоев, где <tex>n</tex> - количество входов.
 
|proof=  
 
|proof=  
 
Докажем данное утверждение по принципу математической индукции.  
 
Докажем данное утверждение по принципу математической индукции.  
  
−
Базой индукции будет <tex> n = 2 </tex>.
+
'''База индукции''':
  
−
Пусть <tex> S(n) = 2n - 3 </tex> - количество слоев в сети сортировки размера n.  
+
При <tex> n = 2 </tex>    <tex> ( 2\cdot2 - 3 = 1) </tex>, что верно.  
  
−
Шаг индукции:  
+
'''Шаг индукции''':  
  
−
При построении <tex>(n + 1)</tex>-й сортирующей сети, выносим сортирующую сеть, содержащую <tex>n</tex> компараторов и добавляем к ней компараторы: <tex>[n + 1; n], [n; n - 1]\dots[3; 2], [2; 1] </tex>.  
+
Пусть <tex> S(n) = 2n - 3 </tex> — количество слоев в сети сортировки.
 +
 
 +
При переходе от <tex>n</tex>-й сортирующей сети к <tex>(n + 1)</tex>-й, добавляем дополнительный вход, который содержит <tex> n </tex> компараторов со своим "соседом", <tex> n - 2 </tex> из которых выполняются одновременно с компараторами из уровня <tex> n - 1 </tex>. Заметим, что два <tex> 2 </tex> компаратора не участвовали во вкладе в слои. Тогда можно заметить, что <tex> S(n + 1) = S(n) + 2 </tex>.
 +
Данное рекуррентное соотношение имеет решение <tex> S(n) = 2n - 3 </tex>. Что и требовалось доказать.
  
−
Подсчитаем количество компараторов: <tex> S(n + 1) = n + n - 1 = 2n - 1 </tex> , заметим, что данное количество слоев удовлетворяет нашему шагу индукции <tex>(S(n + 1) = 2(n + 1) - 3 = 2n + 2 - 3 = 2n - 1)</tex>
 
 
}}
 
}}
  
 +
Сортировка для <tex> n = 6 </tex>
 
[[Файл:Parralelsort.png‎]]
 
[[Файл:Parralelsort.png‎]]
  
Строка 42: Строка 45:
 
Теорема
 
Теорема
 
|statement=
 
|statement=
−
В результирующей сети будет <tex>\dfrac{n(n - 1)}{2}</tex> компараторов.
+
В результирующей сети будет <tex>n - 1</tex> слой, где <tex> n </tex> — количество входов.
 
|proof=  
 
|proof=  
 
Воспользуемся принципом математической индукции.
 
Воспользуемся принципом математической индукции.
  
−
Базой индукции будет <tex> n = 2 </tex>  
+
'''База индукции''':
 +
 
 +
<tex> n = 2 </tex> (<tex> 2 - 1 = 1 </tex>)
  
−
Шаг индукции:
+
'''Шаг индукции''':
  
−
Рассмотрим метод построения сетей для сортировок выбором.  
+
Пусть <tex> S(n) </tex> - количество слоев в сети сортировки с <tex> n </tex> входами.
  
−
Пусть <tex> S(n) </tex> - количество компараторов в сети сортировки с <tex> n </tex> входами, тогда для получения <tex>(n + 1)</tex>-й сети сортировки надо к предыдущей добавить компараторы: <tex>[n + 1; 1], [n; 1]\dots[3; 1], [2; 1] </tex>.  
+
При переходе от <tex>n</tex>-й сортирующей сети к <tex>(n + 1)</tex>-й, добавляем <tex> n - 1 </tex> компаратор, которые являются одним слоем. Тем самым получили рекуррентное соотношение:
 +
<tex> S(n + 1) = S(n) + 1 </tex> с начальными данными (<tex>S(2) = 1</tex>). Решением данного рекуррентного соотношения является <tex> S(n) = n - 1 </tex>. Что и требовалось доказать
  
−
Подсчитаем общее количество компараторов: <tex>S(n + 1) = \dfrac{n(n - 1)}{2} + n = \dfrac{n(n + 1)}{2} </tex>, заметим, что данное количество компараторов удовлетворяет нашему шагу индукции.
 
 
}}
 
}}
−
[[Файл:Choosesortparralel.png‎]]
 
  
 
==См.также==
 
==См.также==

Версия 21:01, 19 мая 2015

Рассмотрим модели сортирующих сетей для квадратичных сортировок.

Сортирующие сети с последовательной сортировкой

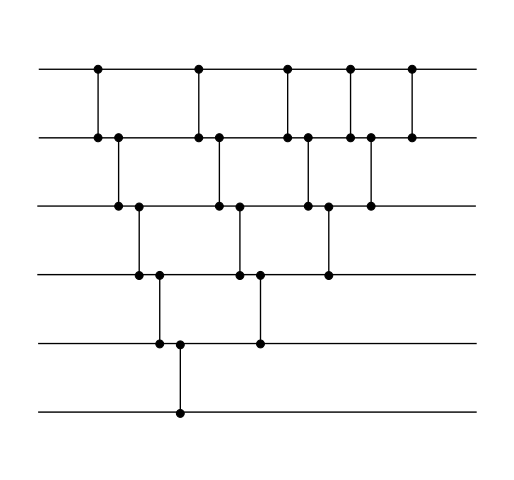
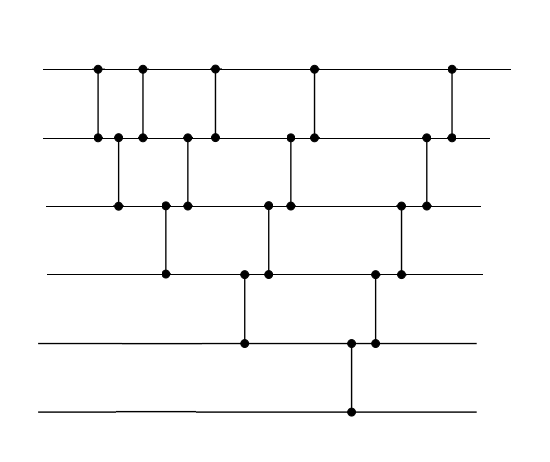
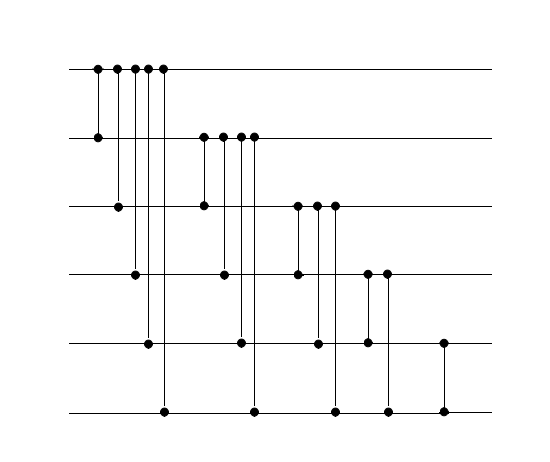
На один слой будем устанавливать только один компаратор. Все последующие сети получаются простым моделированием соответствующих сортировок.

Сортировка пузырьком Сортировка вставками Сортировка выбором
Bubblesort.png Insertsort.png Choosesort.png

Сортирующие сети с параллельной сортировкой

На один слой будем устанавливать несколько компараторов.

Сортировка пузырьком и вставками

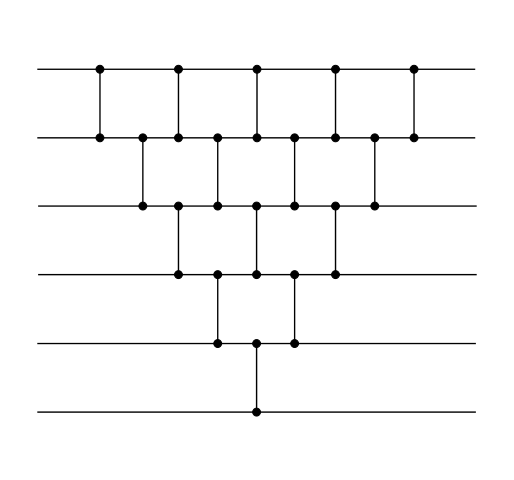
Заметим, если сжать последовательные сортирующие сети пузырьком и вставками, то результат будет одним и тем же. Этот факт легко заметить, если сопоставлять компараторы на уровне [math] k [/math] компараторам на уровне [math] k - 2[/math], где ([math] k [/math] — уровень между [math] k - 1 [/math] и [math] k [/math] входом). Тем самым получаем картинку сводящуюся к "треугольнику".

Теорема:
В результирующей сети будет [math](2n - 3)[/math] слоев, где [math]n[/math] - количество входов.
Доказательство:
[math]\triangleright[/math]

Докажем данное утверждение по принципу математической индукции.

База индукции:

При [math] n = 2 [/math] [math] ( 2\cdot2 - 3 = 1) [/math], что верно.

Шаг индукции:

Пусть [math] S(n) = 2n - 3 [/math] — количество слоев в сети сортировки.

При переходе от [math]n[/math]-й сортирующей сети к [math](n + 1)[/math]-й, добавляем дополнительный вход, который содержит [math] n [/math] компараторов со своим "соседом", [math] n - 2 [/math] из которых выполняются одновременно с компараторами из уровня [math] n - 1 [/math]. Заметим, что два [math] 2 [/math] компаратора не участвовали во вкладе в слои. Тогда можно заметить, что [math] S(n + 1) = S(n) + 2 [/math].

Данное рекуррентное соотношение имеет решение [math] S(n) = 2n - 3 [/math]. Что и требовалось доказать.
[math]\triangleleft[/math]

Сортировка для [math] n = 6 [/math] Parralelsort.png

Сортировка выбором

Теорема:
В результирующей сети будет [math]n - 1[/math] слой, где [math] n [/math] — количество входов.
Доказательство:
[math]\triangleright[/math]

Воспользуемся принципом математической индукции.

База индукции:

[math] n = 2 [/math] ([math] 2 - 1 = 1 [/math])

Шаг индукции:

Пусть [math] S(n) [/math] - количество слоев в сети сортировки с [math] n [/math] входами.

При переходе от [math]n[/math]-й сортирующей сети к [math](n + 1)[/math]-й, добавляем [math] n - 1 [/math] компаратор, которые являются одним слоем. Тем самым получили рекуррентное соотношение:

[math] S(n + 1) = S(n) + 1 [/math] с начальными данными ([math]S(2) = 1[/math]). Решением данного рекуррентного соотношения является [math] S(n) = n - 1 [/math]. Что и требовалось доказать
[math]\triangleleft[/math]

См.также

Источники информации

  • Дональд Э. Кнут. Искусство программирования. Том 3. Сортировка и Поиск. стр. 238— ISBN 0-201-89685-0
  • Кормен, Томас Х.,Рональд Л., Штайн, Клифорд. Глава 27. Сортирующие сети // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-e издание. — М.: «Вильямс», 2005. — С. 799 - 822. — ISBN 5-8459-0857-4.
  • Википедия - Сети сортировки
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Сортирующие_сети_для_квадратичных_сортировок&oldid=46696»