Статистики на отрезках. Корневая эвристика — различия между версиями
Shersh (обсуждение | вклад) м (→Запрос на изменение элемента) |
|||
| (не показано 16 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Корневая эвристика (Sqrt-декомпозиция)''' {{---}} это подход к реализации ассоциативных операций (например, суммирование элементов, нахождение минимума/максимума и т.д.) над идущими подряд элементами некоторого множества за <tex> O(\sqrt n)</tex>. | + | '''Корневая эвристика (Sqrt-декомпозиция)''' {{---}} это подход к реализации ассоциативных операций (например, суммирование элементов, нахождение минимума/максимума и т.д.) над идущими подряд элементами некоторого множества размера <tex>n</tex> за <tex> O(\sqrt n)</tex>. |
== Построение == | == Построение == | ||
| Строка 12: | Строка 12: | ||
Пример реализации построения массива <tex>B</tex> для операции <tex> \circ </tex>: | Пример реализации построения массива <tex>B</tex> для операции <tex> \circ </tex>: | ||
<code> | <code> | ||
| − | build() | + | '''void''' build(): |
'''for''' i = 0 ... cnt | '''for''' i = 0 ... cnt | ||
B[i] = neutral <font color=green>// neutral {{---}} нейтральный элемент для операции <tex> \circ </tex> </font> | B[i] = neutral <font color=green>// neutral {{---}} нейтральный элемент для операции <tex> \circ </tex> </font> | ||
'''for''' i = 0 ... n - 1 | '''for''' i = 0 ... n - 1 | ||
B[i / len] = B[i / len] <tex> \circ </tex> A[i] | B[i / len] = B[i / len] <tex> \circ </tex> A[i] | ||
| − | |||
</code> | </code> | ||
| Строка 35: | Строка 34: | ||
<code> | <code> | ||
| − | query('''int''' l, '''int''' r) | + | '''T''' query('''int''' l, '''int''' r): |
left = l / len | left = l / len | ||
right = r / len | right = r / len | ||
end = (left + 1) * len - 1 | end = (left + 1) * len - 1 | ||
| − | res = neutral <font color=green> //neutral {{---}} нейтральный элемент для операции <tex> \circ </tex> </font> | + | res = neutral <font color=green> // neutral {{---}} нейтральный элемент для операции <tex> \circ </tex> </font> |
'''if''' left == right | '''if''' left == right | ||
'''for''' i = l ... r | '''for''' i = l ... r | ||
| Строка 50: | Строка 49: | ||
'''for''' i = right * len ... r | '''for''' i = right * len ... r | ||
res = res <tex> \circ </tex> A[i] | res = res <tex> \circ </tex> A[i] | ||
| − | |||
</code> | </code> | ||
| Строка 58: | Строка 56: | ||
== Запрос на изменение элемента == | == Запрос на изменение элемента == | ||
Реализация данного запроса будет зависеть от того, имеет ли операция, для которой сделано построение, обратную операцию и обладает ли она свойством коммутативности. | Реализация данного запроса будет зависеть от того, имеет ли операция, для которой сделано построение, обратную операцию и обладает ли она свойством коммутативности. | ||
| − | * если оба условия выполняются, то запрос на изменение элемента можно сделать за <tex>O(1)</tex> времени | + | * если оба условия выполняются, то запрос на изменение элемента можно сделать за <tex>O(1)</tex> времени, |
* если хотя бы одно из условий не выполняется, то запрос на изменение элемента можно сделать за <tex>O(\sqrt{n})</tex> времени. | * если хотя бы одно из условий не выполняется, то запрос на изменение элемента можно сделать за <tex>O(\sqrt{n})</tex> времени. | ||
| Строка 65: | Строка 63: | ||
Примеры реализации: | Примеры реализации: | ||
| − | <tex>p</tex> {{---}} номер элемента из массива <tex>A</tex>, который необходимо заменить | + | * <tex>p</tex> {{---}} номер элемента из массива <tex>A</tex>, который необходимо заменить, |
| + | * <tex>\mathtt{newValue}</tex> {{---}} новое значение для данного элемента. | ||
Запрос на изменение элемента для операции, у которой есть обратная операция, и выполняется свойство коммутативности: | Запрос на изменение элемента для операции, у которой есть обратная операция, и выполняется свойство коммутативности: | ||
<code> | <code> | ||
| − | set('''int''' p, ''' | + | '''function''' set('''int''' p, '''T''' newValue): |
tmp = B[p / len] <tex> \circ </tex> inverse(A[p]) <font color=green>// inverse(A[p]) {{---}} обратный элемент</font> | tmp = B[p / len] <tex> \circ </tex> inverse(A[p]) <font color=green>// inverse(A[p]) {{---}} обратный элемент</font> | ||
A[p] = newValue | A[p] = newValue | ||
B[p / len] = tmp <tex> \circ </tex> newValue | B[p / len] = tmp <tex> \circ </tex> newValue | ||
| − | |||
</code> | </code> | ||
| + | |||
| + | '''Замечание:''' важность наличия свойства коммутативности подчеркивает следующий контрпример. Известно, что умножение матриц не коммутативно. Возьмем блок <tex> b_0 </tex>, как показано на иллюстрации выше, со следующими значениями: | ||
| + | |||
| + | <tex> b_0 = \begin{pmatrix} 27 & 32 \\ 42 & 50 \end{pmatrix} </tex> , | ||
| + | |||
| + | <tex> a_0 = \begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix} </tex> , | ||
| + | |||
| + | <tex> a_1 = \begin{pmatrix} 2 & 2 \\ 2 & 3 \end{pmatrix} </tex> , | ||
| + | |||
| + | <tex> a_2 = \begin{pmatrix} 3 & 3 \\ 3 & 4 \end{pmatrix} </tex>. | ||
| + | |||
| + | Пусть необходимо изменить значение матрицы <tex> a_1 </tex> на следующее: | ||
| + | |||
| + | <tex> \mathtt{newValue} = a_1 = \begin{pmatrix} 4 & 4 \\ 4 & 5 \end{pmatrix} </tex>. | ||
| + | |||
| + | Тогда значения <tex> a_1^{-1} </tex>, <tex> tmp </tex> и новое значение <tex> a_1 </tex> таковы : | ||
| + | |||
| + | |||
| + | <tex> a_1^{-1} = \begin{pmatrix} 1,5 & -1 \\ -1 & 1 \end{pmatrix} </tex>, | ||
| + | |||
| + | <tex> tmp = b \cdot a_1^{-1} = \begin{pmatrix} 8,5 & 5 \\ 13 & 8 \end{pmatrix} </tex> , | ||
| + | |||
| + | <tex> a_1 = \begin{pmatrix} 4 & 4 \\ 4 & 5 \end{pmatrix} </tex>. | ||
| + | |||
| + | Тогда новое значение <tex> b_0 </tex> следующее: | ||
| + | |||
| + | |||
| + | <tex> b_0 = \begin{pmatrix} 54 & 59 \\ 84 & 92 \end{pmatrix} </tex>. | ||
| + | |||
| + | Хотя правильный результат: <tex> b_0 = \begin{pmatrix} 51 & 60 \\ 78 & 92 \end{pmatrix} </tex>. | ||
Запрос на изменение элемента для операции, у которой хотя бы одно из условий не выполняется: | Запрос на изменение элемента для операции, у которой хотя бы одно из условий не выполняется: | ||
<code> | <code> | ||
| − | set('''int''' p, ''' | + | '''function''' set('''int''' p, '''T''' newValue): |
index = len * (p / len) | index = len * (p / len) | ||
A[p] = newValue | A[p] = newValue | ||
| Строка 86: | Строка 114: | ||
'''for''' i = index ... index + len - 1 | '''for''' i = index ... index + len - 1 | ||
B[p / len] = B[p / len] <tex> \circ </tex> A[i] | B[p / len] = B[p / len] <tex> \circ </tex> A[i] | ||
| − | |||
</code> | </code> | ||
| Строка 94: | Строка 121: | ||
==Источники информации== | ==Источники информации== | ||
| − | * [http://www.e-maxx.ru/algo/sqrt_decomposition Maximal:: algo:: Sqrt - декомпозиция] | + | * [http://www.e-maxx.ru/algo/sqrt_decomposition Maximal:: algo:: Sqrt-декомпозиция] |
* [http://habrahabr.ru/post/138946/#habracut Sqrt-декомпозиция (корневая оптимизация)] | * [http://habrahabr.ru/post/138946/#habracut Sqrt-декомпозиция (корневая оптимизация)] | ||
Версия 11:19, 10 мая 2015
Корневая эвристика (Sqrt-декомпозиция) — это подход к реализации ассоциативных операций (например, суммирование элементов, нахождение минимума/максимума и т.д.) над идущими подряд элементами некоторого множества размера за .
Содержание
Построение
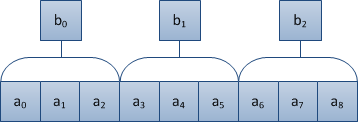
Пусть дан массив размерности . Cделаем следующие действия:
- разделим массив на блоки длины ,
- в каждом блоке заранее посчитаем необходимую операцию,
- результаты подсчета запишем в массив размерности , где — количество блоков.
Пример реализации построения массива для операции :
void build():
for i = 0 ... cnt
B[i] = neutral // neutral — нейтральный элемент для операции
for i = 0 ... n - 1
B[i / len] = B[i / len] A[i]
Построение, очевидно, происходит за времени.
Обработка запроса
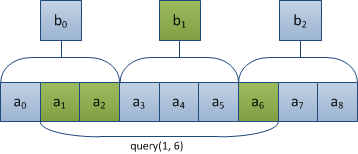
Пусть получен запрос на выполнение операции на отрезке . Отрезок может охватить некоторые блоки массива полностью, а так же не более двух блоков (начальный и конечный) — не полностью.
Таким образом, для того чтобы найти результат операции на отрезке необходимо вручную выполнить ее на "хвостах", а потом выполнить ее для полученного результата и полных блоков, значения которых мы посчитали заранее.
Пример реализации обработки запроса:
— операция, для которой было сделано построение.
T query(int l, int r):
left = l / len
right = r / len
end = (left + 1) * len - 1
res = neutral // neutral — нейтральный элемент для операции
if left == right
for i = l ... r
res = res A[i]
else
for i = l ... end
res = res A[i]
for i = left + 1 ... right - 1
res = res B[i]
for i = right * len ... r
res = res A[i]
Размер каждого из "хвостов", очевидно, не превосходит длины блока , а количество блоков не превосходит . Поскольку было выбрано равным , а было выбрано равным , то для выполнения операции на отрезке понадобится времени.
Запрос на изменение элемента
Реализация данного запроса будет зависеть от того, имеет ли операция, для которой сделано построение, обратную операцию и обладает ли она свойством коммутативности.
- если оба условия выполняются, то запрос на изменение элемента можно сделать за времени,
- если хотя бы одно из условий не выполняется, то запрос на изменение элемента можно сделать за времени.
Примеры реализации:
- — номер элемента из массива , который необходимо заменить,
- — новое значение для данного элемента.
Запрос на изменение элемента для операции, у которой есть обратная операция, и выполняется свойство коммутативности:
function set(int p, T newValue):
tmp = B[p / len] inverse(A[p]) // inverse(A[p]) — обратный элемент
A[p] = newValue
B[p / len] = tmp newValue
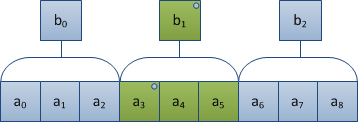
Замечание: важность наличия свойства коммутативности подчеркивает следующий контрпример. Известно, что умножение матриц не коммутативно. Возьмем блок , как показано на иллюстрации выше, со следующими значениями:
,
,
,
.
Пусть необходимо изменить значение матрицы на следующее:
.
Тогда значения , и новое значение таковы :
,
,
.
Тогда новое значение следующее:
.
Хотя правильный результат: .
Запрос на изменение элемента для операции, у которой хотя бы одно из условий не выполняется:
function set(int p, T newValue):
index = len * (p / len)
A[p] = newValue
B[p / len] = neutral // neutral — нейтральный элемент для операции
for i = index ... index + len - 1
B[p / len] = B[p / len] A[i]