Стохастическое вложение соседей с t-распределением
Стохастическое вложение соседей с t-распределением (англ. t-Distributed Stochastic Neighbor Embedding, t-SNE) — метод визуализации данных высокой размерности с помощью представления каждой точки данных в двух или трехмерном пространстве, являющийся модификацией метода стохастического вложения соседей.
Содержание
Стохастическое вложение соседей
Пусть стоит задача вложить множество точек в пространстве высокой размерности в пространство низкой размерности. Обозначим множество точек в пространстве низкой размерности, которые получаются после вложения через . Стохастическое вложение соседей (англ. Stochastic Neighbor Embedding, SNE) конвертирует расстояния в Евклидовом пространстве высокой размерности между точками в условные вероятности . — вероятность, что точка выберет в качестве своего соседа точку среди остальных точек данных. Будем считать, что вероятность для точки найти соседа падает с увеличением расстояния от точки в соответствии с распределением Гаусса[4] с нулевым математическим ожиданием и стандартным отклонением . В соответствии с этим выражается как
.
Теперь определим похожие вероятности для пространства низкой размерности, куда вкладываются точки пространства высокой размерности.
.
Данные вероятности получаются из тех же самых предложений, что были сделаны для пространства высокой размерности, за исключением того, что все распределения Гаусса имеют стандартное отклонение для всех точек.
Если удастся хорошо вложить одно пространство в другое, должны стать похожими на . В связи с этим SNE пытается уменьшить разницу в распределении вероятностей. Стандартной мерой для измерения различия вероятностей служит дивергенция Кульбака-Лейблера[5]:
.
В данном случае имеем распределений. Тогда целевую функцию[6], которую будем оптимизировать, определим как сумму соответствующих дивергенций Кульбака-Лейблера. То есть:
.
Дивергенция Кульбака-Лейблера не является симметричной мерой, поэтому, например, вложение близких точек в удаленные даёт гораздо большее значение ошибки, чем вложение далеких точек в близкие. Другими словами, целевая функция нацелена на сохранение локальной структуры вокруг точек.
Параметры подбираются следующим образом. Каждое значение параметра порождает свое распределение вероятностей . Это распределение имеет энтропию[7] , которая возрастает с ростом . В самом алгоритме вычисляются с помощью вещественного двоичного поиска по заранее заданной пользователем величине, называемой перплексией[8]: .
Изначально точки сэмплируют в пространстве низкой размерности в соответствии с распределением Гаусса с маленьким стандартным отклонением с математическим ожиданием в нуле, далее идет оптимизация целевой функции. Она проводится методом градиентного спуска. Градиент равен:
Физическая интерпретация
Есть следующая физическая интерпретация модели. В пространстве низкой размерности натянуты пружины между каждой парой точек и , действующие в направлении . Пружины могут притягивать или отталкивать точки в зависимости от расстояния между ними. Сила, прикладываемая пружиной, пропорциональна её длине и жесткости[9] . Оптимизация функционала в данной интерпретации эквивалентна поиску положения точек, в котором будет наблюдаться равновесие сил.
Симметричное стохастическое вложение соседей
Следующая модификация SNE носит название симметричное стохастическое вложение соседей (англ. Symmetric Stochastic Neighbor Embedding, Symmetric SNE), которая будет использоваться дальше в t-SNE. Симметричный SNE в качестве альтернативы использует совместные вероятности вместо условных. Теперь:
.
Очевидным образом можно определить :
,
но то же решение для привело бы к проблеме, что для выброса будет очень маленькой для любого . Таким образом, будет почти нулевой соответствующая дивергенция Кульбака-Лейблера для любого распределения . Это означало бы, что положение точки определялось бы очень неточно относительно положения других точек и не было бы особой разницы в том, где она расположена.
Таким образом, в симметричном SNE в качестве рассматривается следующая величина:
.
Очевидный плюс в том, что для всех точек, что хорошо скажется на выбросах. А также теперь , .
Авторы утверждают, что симметричный SNE вкладывает данные в пространство низкой размерности почти так же как и ассиметричный, а иногда даже лучше.
Градиент при таком подходе принимает вид: .
Проблема скученности
Необходимо понимать, что невозможно абсолютно точно моделировать расстояния между точками пространства высокой размерности в низком. Например, в десятимерном пространстве существует равноудаленных друг от друга точек, в то время как на плоскости может быть максимум равноудаленные точки.
При использовании обычного SNE возникает проблема, которая вытекает из разного распределения вероятностей в пространствах высокой и низкой размерностей. Пусть есть некоторое пространство высокой размерности. Пусть точки равномерно распределены в нем вокруг точки в некотором шаре с радиусом . Заметим, что, чем больше размерность пространства, тем больше точек попадет рядом с границей шара, поэтому количество близких к точек с ростом размерности будет убывать. Теперь попытаемся вложить данное пространство в плоскость. Пусть точки перешли в точки на плоскости. Заметим, что если попытаться вложить точки в круг радиуса с центром в точке образуется большое количество маленьких расстояний между точками , т.к. объем сферы в высокомерном пространстве несопоставим с площадью круга на плоскости. Таким образом, если мы хотим правильно моделировать маленькие расстояния на плоскости, следовало бы поместить удаленные от точки ещё дальше, чем в исходном пространстве. Но в таком случае, вспоминая физическую интерпретацию, на соответствующие им точки будет действовать небольшая сила притяжения к точке . Принимая во внимание, что точек наподобие в реальной выборке данных будет достаточно много, их пружины вместе образуют силу, что сожмет все точки в нуле и будет мешать образованию кластеров.
Стохастическое вложение соседей с t-распределением
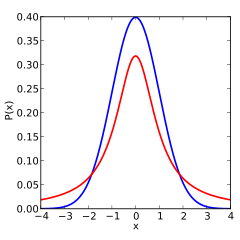
Чтобы избежать проблемы скученности, было решено использовать в пространстве низкой размерности t-распределение Стьюдента с одной степенью свободы[10] вместо распределения Гаусса. Данное распределение очень похоже на распределение Гаусса, но имеет большую вероятностную массу на участках, отдаленных от нуля (Рис. 2.), что решает описанную выше проблему, т.к. теперь удаленные точки лучше отталкиваются.
В связи с заменой распределения определяется следующим образом:
.
Еще одно свойство данного распределения состоит в том, что описывает закон обратных квадратов[11] для далеких точек в пространстве низкой размерности, что позволяет думать не об отдельных точках, а о кластерах, которые будут взаимодействовать между собой как отдельные точки.
После замены распределения изменился градиент целевой функции, теперь он равен:
.
Оптимизации t-SNE
В t-SNE используется 2 основные оптимизации:
- Первая оптимизация называется "раннее сжатие". В данной оптимизации на ранних итерациях оптимизации к целевой функции добавляется -штраф на расстояния в пространстве низкой размерности, что влечет за собой сжатие всех точек в нуле. В связи с этим кластерам будет легче переходить друг через друга, чтобы правильно расположиться в пространстве.
- Вторая оптимизация называется "раннее преувеличение". В данной оптимизации на ранних итерациях умножаются на некоторое положительное число, например на . Так как остаются теми же самыми, они слишком маленькие, чтобы моделировать соответствующие . Как следствие, образуются очень плотные кластера, которые широко раскиданы в пространстве низкой размерности. Это создает много пустого пространства, которое используется кластерами, чтобы легко менять и находить наилучшее взаимное расположение.
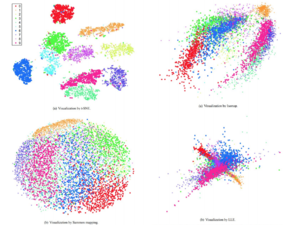
На Рис. 3 представлена визуализация работы t-SNE, на которой видны эффекты от применения приведенных выше оптимизаций.