Суффиксный бор — различия между версиями
Iloskutov (обсуждение | вклад) (→Свойства: более удачный пример для O(n^2) вершин; элементы списка со строчной буквы) |
Penguinni (обсуждение | вклад) м |
||
| (не показано 7 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| − | '''Суффиксный бор''' (англ. ''suffix trie'') | + | '''Суффиксный бор''' (англ. ''suffix trie'') — [[бор]], содержащий все суффиксы данной строки. |
| − | По определению, в суффиксном боре для строки <tex>s</tex> (где <tex>|s| = n</tex>) содержатся все строки <tex>s[1 \ | + | По определению, в суффиксном боре для строки <tex>s</tex> (где <tex>|s| = n</tex>) содержатся все строки <tex>s[1 \ldots n], \dotsc, s[n \ldots n]</tex>. Заметим, что если в суффиксном боре находится строка <tex>s[i \ldots n]</tex>, то все её префиксы <tex>s[i \ldots j]</tex> (<tex>i \leqslant j \leqslant n</tex>) уже содержатся в боре. |
==Применение== | ==Применение== | ||
| + | Суффиксный бор можно использовать для поиска подстроки в строке <tex>s</tex> тем же образом, что и для [[Бор#Поиск строки в бору|поиска строки в боре]]. Чтобы бор формально содержал все подстроки <tex>s</tex>, нужно пометить все его вершины терминальными, при этом корень будет соответствовать пустой строке <tex>\varepsilon</tex>. | ||
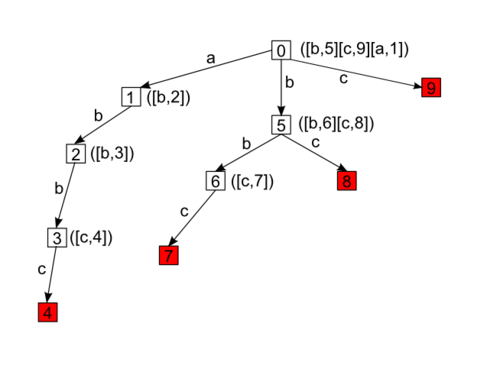
[[Файл:Syffix_trie_1.png|500px|thumb|center|Суффиксный бор для строки <tex>abbc</tex>]] | [[Файл:Syffix_trie_1.png|500px|thumb|center|Суффиксный бор для строки <tex>abbc</tex>]] | ||
| − | |||
| − | ==Свойства== | + | === Свойства === |
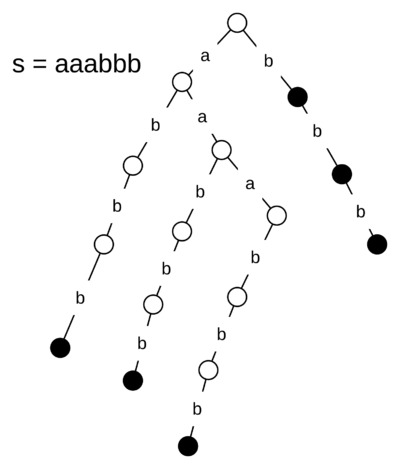
| − | [[Файл:aaabbb-suftrie.png|мини| | + | [[Файл:aaabbb-suftrie.png|мини|400px|Суффиксный бор для строки «aaabbb»]] |
Суффиксный бор для строки <tex>s</tex>: | Суффиксный бор для строки <tex>s</tex>: | ||
* можно использовать для поиска образца <tex>p</tex> в строке <tex>s</tex> за время <tex>O(|p|)</tex>, | * можно использовать для поиска образца <tex>p</tex> в строке <tex>s</tex> за время <tex>O(|p|)</tex>, | ||
* можно построить за время <tex>O(n^2)</tex>, последовательно добавив все суффиксы <tex>s</tex>, | * можно построить за время <tex>O(n^2)</tex>, последовательно добавив все суффиксы <tex>s</tex>, | ||
| − | * имеет порядка <tex>n^2</tex> вершин в худшем случае. Например, для строки <tex>a^n b^n</tex> суффиксный бор будет содержать: | + | * имеет порядка <tex>n^2</tex> вершин в худшем случае. Например, для строки <tex>a^n b^n</tex> суффиксный бор будет содержать: |
| − | + | : <tex>1</tex> корневую вершину, | |
| − | + | : <tex>n</tex> вершин для суффикса <tex>b^n</tex>, | |
| − | + | : <tex>n</tex> вершин для подстроки <tex>a^n</tex>, у каждой по <tex>n</tex> вершин для соответствующего суффикса <tex>b^n</tex>. | |
| − | + | <ul style="list-style: none;"><li>итого <tex>1 + 2n + n^2 = (n+1)^2 = \theta(n^2)</tex> вершин.</ul> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''function''' build(s : '''string''') | + | === Реализация === |
| − | + | Зададим бор его корнем: | |
| − | + | <code style="display: inline-block"> | |
| − | + | '''struct''' Trie: | |
| − | + | '''Node''' root | |
| + | </code> | ||
| + | По каждому символу будем хранить переход в соответствующую вершину: | ||
| + | <code style="display: inline-block"> | ||
| + | '''struct''' Node: | ||
| + | '''map<char, Node>''' children | ||
| + | </code> | ||
| + | При добавлении узла будем идти вниз по сыновьям и добавлять их, если необходимо: | ||
| + | <code style="display: inline-block"> | ||
| + | '''function''' add(s : '''string'''): | ||
| + | '''Node''' current = root | ||
| + | '''for''' c '''in''' s | ||
| + | '''if''' current.children[c] == <tex>\varnothing</tex> | ||
| + | current.children[c] = Node() | ||
| + | current = current.children[c] | ||
| + | </code> | ||
| + | Чтобы построить суффиксный бор для некоторой строки, последовательно добавим в пустой бор все её суффиксы: | ||
| + | <code style="display: inline-block"> | ||
| + | '''function''' build(s : '''string'''): | ||
| + | root = Node() | ||
| + | '''int''' n = s.size | ||
| + | '''for''' i = 0 '''to''' n - 1 | ||
| + | add(s[i..n]) | ||
| + | </code> | ||
| − | ==Оценки использования памяти== | + | === Оценки использования памяти === |
Пусть мы построили суффиксный бор для строки <tex>s \in \Sigma^*</tex> (<tex>|s| = n</tex>). Из третьего свойства следует, что если хранить переходы суффиксного бора из каждой вершины как массив размера <tex>|\Sigma|</tex> (по каждому символу — переход), то потребуется <tex>O(n^2 |\Sigma|)</tex> памяти. | Пусть мы построили суффиксный бор для строки <tex>s \in \Sigma^*</tex> (<tex>|s| = n</tex>). Из третьего свойства следует, что если хранить переходы суффиксного бора из каждой вершины как массив размера <tex>|\Sigma|</tex> (по каждому символу — переход), то потребуется <tex>O(n^2 |\Sigma|)</tex> памяти. | ||
Однако, заметим, что число ветвлений в не превышает числа листьев, что, в свою очередь, не превышает количества суффиксов. Количество суффиксов — <tex>n</tex>, а значит число вершин, из которых ведет больше одного перехода, <tex>O(n)</tex>. Поэтому, если в неветвящихся вершинах хранить только символ перехода и ребенка, то можно получить оценку <tex>O(n^2 + n|\Sigma|)</tex>. Улучшением суффиксного бора, расходующим всего <tex>O( n|\Sigma|)</tex> памяти, является [[сжатое суффиксное дерево]]. | Однако, заметим, что число ветвлений в не превышает числа листьев, что, в свою очередь, не превышает количества суффиксов. Количество суффиксов — <tex>n</tex>, а значит число вершин, из которых ведет больше одного перехода, <tex>O(n)</tex>. Поэтому, если в неветвящихся вершинах хранить только символ перехода и ребенка, то можно получить оценку <tex>O(n^2 + n|\Sigma|)</tex>. Улучшением суффиксного бора, расходующим всего <tex>O( n|\Sigma|)</tex> памяти, является [[сжатое суффиксное дерево]]. | ||
Версия 20:41, 22 марта 2017
Суффиксный бор (англ. suffix trie) — бор, содержащий все суффиксы данной строки.
По определению, в суффиксном боре для строки (где ) содержатся все строки . Заметим, что если в суффиксном боре находится строка , то все её префиксы () уже содержатся в боре.
Содержание
Применение
Суффиксный бор можно использовать для поиска подстроки в строке тем же образом, что и для поиска строки в боре. Чтобы бор формально содержал все подстроки , нужно пометить все его вершины терминальными, при этом корень будет соответствовать пустой строке .
Свойства
Суффиксный бор для строки :
- можно использовать для поиска образца в строке за время ,
- можно построить за время , последовательно добавив все суффиксы ,
- имеет порядка вершин в худшем случае. Например, для строки суффиксный бор будет содержать:
- корневую вершину,
- вершин для суффикса ,
- вершин для подстроки , у каждой по вершин для соответствующего суффикса .
- итого вершин.
Реализация
Зададим бор его корнем:
struct Trie: Node root
По каждому символу будем хранить переход в соответствующую вершину:
struct Node: map<char, Node> children
При добавлении узла будем идти вниз по сыновьям и добавлять их, если необходимо:
function add(s : string):
Node current = root
for c in s
if current.children[c] ==
current.children[c] = Node()
current = current.children[c]
Чтобы построить суффиксный бор для некоторой строки, последовательно добавим в пустой бор все её суффиксы:
function build(s : string):
root = Node()
int n = s.size
for i = 0 to n - 1
add(s[i..n])
Оценки использования памяти
Пусть мы построили суффиксный бор для строки (). Из третьего свойства следует, что если хранить переходы суффиксного бора из каждой вершины как массив размера (по каждому символу — переход), то потребуется памяти. Однако, заметим, что число ветвлений в не превышает числа листьев, что, в свою очередь, не превышает количества суффиксов. Количество суффиксов — , а значит число вершин, из которых ведет больше одного перехода, . Поэтому, если в неветвящихся вершинах хранить только символ перехода и ребенка, то можно получить оценку . Улучшением суффиксного бора, расходующим всего памяти, является сжатое суффиксное дерево.
См. также
Источники информации
- Дэн Гасфилд — Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с: ил.