Теорема Клини (совпадение классов автоматных и регулярных языков) — различия между версиями
м |
(→Источники информации) |
||
| (не показано 16 промежуточных версий 9 участников) | |||
| Строка 1: | Строка 1: | ||
{{Теорема | {{Теорема | ||
|author=Клини | |author=Клини | ||
| − | |statement=Классы автоматных и регулярных языков совпадают. | + | |statement=Классы [[Детерминированные_конечные_автоматы#Автоматные_языки | автоматных]] и [[Регулярные языки:_два определения_и_их_эквивалентность#REG1 | регулярных]] языков совпадают. |
|proof= | |proof= | ||
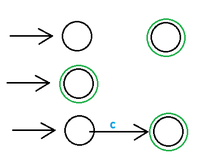
[[Файл:Reg0.png|200px|thumb|right|Автоматы для регулярных языков нулевого поколения]] | [[Файл:Reg0.png|200px|thumb|right|Автоматы для регулярных языков нулевого поколения]] | ||
| Строка 7: | Строка 7: | ||
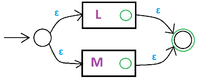
[[Файл:concat.png|200px|thumb|right|Автомат для конкатенации двух регулярных языков]] | [[Файл:concat.png|200px|thumb|right|Автомат для конкатенации двух регулярных языков]] | ||
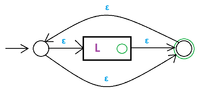
[[Файл:Klenee.png|200px|thumb|right|Автомат для замыкания Клини регулярного языка]] | [[Файл:Klenee.png|200px|thumb|right|Автомат для замыкания Клини регулярного языка]] | ||
| − | |||
| − | + | *<tex>\mathrm{REG} \subseteq \mathrm{AUT}</tex>. | |
| − | + | Для доказательства будем строить автоматы, допускающие регулярные языки (см. картинки справа). При этом будем использовать индукцию по номеру поколения регулярного языка. | |
| − | Для | ||
| − | |||
| − | |||
| − | |||
| − | + | '''База''' | |
| − | Для этого достаточно научиться строить автоматы для следующих языков (<tex> | + | :<tex>n = 0</tex>. |
| − | + | :Для этого достаточно построить автоматы для трех языков: | |
| − | + | :#<tex>L = \varnothing</tex>, | |
| − | + | :#<tex>L = \left\{\varepsilon \right\}</tex>, | |
| + | :#<tex>L = \left\{c \right\}</tex>. | ||
| + | |||
| + | '''Индукционный переход''' | ||
| + | :Умеем строить автоматы для языков <tex>n</tex>-ого поколения. Будем строить для <tex>n + 1</tex>. | ||
| + | :Для этого достаточно научиться строить автоматы для следующих языков (<tex>L, M \in \mathrm{R_n}</tex>): | ||
| + | :#<tex>L^\prime = L \cup M</tex>, | ||
| + | :#<tex>L^\prime = LM</tex>, | ||
| + | :#<tex>L^\prime = L^*</tex>. | ||
Заметим, что по предположению индукции автоматы для <tex>L, M</tex> могут быть построены. | Заметим, что по предположению индукции автоматы для <tex>L, M</tex> могут быть построены. | ||
| − | Итого, мы можем по регулярному выражению построить автомат, допускающий тот же язык. | + | '''Итого''', мы можем по регулярному выражению построить автомат, допускающий тот же язык. |
| − | + | <br> | |
| + | *<tex>\mathrm{AUT} \subseteq \mathrm{REG}</tex>. | ||
Для доказательства будем строить регулярное выражение, допускающее язык, заданный каким-то автоматом. Пусть задан автомат <tex>A</tex> с набором состояний <tex>Q = \left\{1, 2, \dots n \right\}</tex>. | Для доказательства будем строить регулярное выражение, допускающее язык, заданный каким-то автоматом. Пусть задан автомат <tex>A</tex> с набором состояний <tex>Q = \left\{1, 2, \dots n \right\}</tex>. | ||
| Строка 32: | Строка 36: | ||
Определим регулярные выражения, задающие следующие множества слов: | Определим регулярные выражения, задающие следующие множества слов: | ||
| − | <tex>\xi_{ijk} = \left\{ s \mid | + | :<tex>\xi_{ijk} = \left\{ s \mid \langle i,s \rangle \vdash^* \langle j, \varepsilon \rangle \right\} </tex>, причем в качестве промежуточных вершин выступают только такие, у которых номер не более <tex>k</tex>. |
| − | + | <br> | |
Построим эти регулярные выражения: | Построим эти регулярные выражения: | ||
| − | + | #<tex>\xi_{ii0} = (c_1 \mid \dots \mid c_l)^*</tex> , где <tex>c_1, c_2, \dots c_l</tex> символы, по которым есть переход из состояния <tex>i</tex> в него же самого. | |
| − | + | #<tex>\xi_{ij0} = c_1 \mid \dots \mid c_l</tex>, где <tex>c_1, c_2, \dots c_l</tex> символы, по которым есть переход из состояния <tex>i</tex> в состояние <tex>j</tex>. | |
| − | *<tex>\xi_{ijk} = \xi_{ij{k-1}} \mid \xi_{ik{k-1}} (\xi_{kk{k-1}})^* \xi_{kj{k-1}}</tex> | + | #<tex>\xi_{iik} = (\xi_{ii{k-1}} \mid \xi_{ik{k-1}} (\xi_{kk{k-1}})^* \xi_{ki{k-1}} )^*</tex>. |
| − | + | #<tex>\xi_{ijk} = \xi_{ij{k-1}} \mid \xi_{ik{k-1}} (\xi_{kk{k-1}})^* \xi_{kj{k-1}}</tex>. | |
| + | <br> | ||
Теперь нетрудно задать регулярное выражение для всего языка: | Теперь нетрудно задать регулярное выражение для всего языка: | ||
| − | <tex>\varphi = \xi_{s{t_1}n} \mid \xi_{s{ | + | :<tex>\varphi = \xi_{s{t_1}n} \mid \xi_{s{t_2}n} \mid \dots \mid \xi_{s{t_r}n}</tex>, где <tex>s</tex> — стартовое состояние, а <tex>t_1, t_2, \dots t_r</tex> — терминальные состояния исходного автомата. |
| − | Таким образом мы построили по автомату регулярное выражение, допускающее тот же самый язык. | + | '''Таким образом''', мы построили по автомату регулярное выражение, допускающее тот же самый язык. |
}} | }} | ||
| + | |||
| + | == См. также == | ||
| + | * [[Регулярные языки: два определения и их эквивалентность]] | ||
| + | * [[Детерминированные конечные автоматы]] | ||
| + | |||
| + | == Источники информации== | ||
| + | * [https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%9A%D0%BB%D0%B8%D0%BD%D0%B8 Википедия {{---}} Теорема Клини] | ||
| + | * ''Хопкрофт Д., Мотвани Р., Ульман Д.'' Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — М.:Издательский дом «Вильямс», 2002. — С. 61.— ISBN 5-8459-0261-4 | ||
| + | |||
| + | |||
| + | [[Категория: Теория формальных языков]] | ||
| + | [[Категория: Автоматы и регулярные языки]] | ||
Версия 19:55, 3 января 2017
| Теорема (Клини): |
Классы автоматных и регулярных языков совпадают. |
| Доказательство: |
Для доказательства будем строить автоматы, допускающие регулярные языки (см. картинки справа). При этом будем использовать индукцию по номеру поколения регулярного языка. База
Индукционный переход
Заметим, что по предположению индукции автоматы для могут быть построены. Итого, мы можем по регулярному выражению построить автомат, допускающий тот же язык.
Для доказательства будем строить регулярное выражение, допускающее язык, заданный каким-то автоматом. Пусть задан автомат с набором состояний . Определим регулярные выражения, задающие следующие множества слов:
|
См. также
Источники информации
- Википедия — Теорема Клини
- Хопкрофт Д., Мотвани Р., Ульман Д. Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — М.:Издательский дом «Вильямс», 2002. — С. 61.— ISBN 5-8459-0261-4