|
|
| Строка 56: |
Строка 56: |
| | | | |
| | }} | | }} |
| | + | |
| | + | ==См. также== |
| | + | * [[Матрица Татта и связь с размером максимального паросочетания в двудольном графе]] |
| | + | * [[Паросочетания: основные определения, теорема о максимальном паросочетании и дополняющих цепях]] |
| | + | * [[Декомпозиция Эдмондса-Галлаи]] |
| | | | |
| | ==Примечания== | | ==Примечания== |
Версия 22:33, 22 ноября 2018
| Определение: |
| [math]\mathrm{odd}({G})[/math] — число нечетных компонент связности в графе [math]{G}[/math], где нечетная компонента (англ. odd component) — это компонента связности, содержащая нечетное число вершин. |
| Определение: |
| Множество Татта графа [math]{G}[/math] — множество [math]S \subset {V_{G}}[/math], для которого выполнено условие: [math]\mathrm{odd}({G} \setminus S) \gt \left\vert S \right\vert[/math] |
Критерий Татта
Пусть [math]{G'}[/math] — граф, полученный из [math]{G}=\langle {V},{E} \rangle[/math] добавлением ребер, при этом в [math]{G'}[/math] нет полного паросочетания, но оно появляется при добавлении любого нового ребра.
Так как новых вершин не добавлялось, то [math]{G'}=\langle {V},{E'}\rangle [/math]
Пусть [math] U = \{ v \in {V}: \deg_{G'} (v) = n - 1 \}[/math].
Очевидно, что [math]\left\vert U \right\vert \ne n[/math], потому что [math]{G'}[/math] — не полный граф.
| Лемма: |
[math]{G'} \setminus U[/math] — объединение несвязных полных графов. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Пусть это не так, тогда существуют вершины [math]x,y,z \in {V} \setminus U[/math], такие что [math]xy, yz \in {E'}[/math], но [math]xz \notin {E'}[/math]. Так как [math]y \notin U[/math], то [math]\exists t \notin U: yt \notin {E'}[/math].
По построению [math]{G'}[/math] в графе [math]{G'}+xz[/math] существует полное паросочетание [math]M_1[/math]. Аналогично, в графе [math]{G'}+yt[/math] существует полное паросочетание [math]M_2[/math]. Так как в [math]{G'}[/math] нет полного паросочетания, то [math]xz \in M_1[/math] и [math]yt \in M_2[/math].
Возможны два случая:
- Вершины [math]x,z[/math] и [math]y,t[/math] лежат в разных полных подграфах графа [math]{G'} \setminus U[/math], обозначим их [math]H_1[/math] и [math]H_2[/math], соответственно.
- Покроем вершины подграфа [math]H_1[/math] паросочетанием [math]M_2[/math], при этом заметим, что ребро [math]xz[/math] не входит в это паросочетание. Аналогично покроем паросочетанием [math]M_1[/math] вершины подрафа [math]H_2[/math] и ребро [math]yt[/math] не войдет в это паросочетание. Если остались непокрытые вершины, то покроем их ребрами из любого паросочетания [math]M_1[/math] или [math]M_2[/math]. Таким образом, мы получим полное паросочетание в графе [math]{G'}[/math], что противоречит его построению.
-
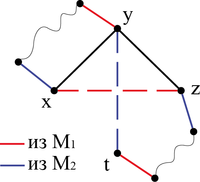 К доказательству 2-ого пункта леммы.
- Вершины [math]x,y,z[/math] и [math]t[/math] лежат в одном подграфе графа [math]{G'} \setminus U[/math].
- Построим граф [math]H[/math], такой что [math]{V_{H}}={V}[/math] и [math]{E_{H}}=M_1 \oplus M_2[/math][1]. Получим, что вершины [math]x,y,z[/math] и [math]t[/math] лежат на каком-то чередующемся цикле из ребер [math]M_1[/math] и [math]M_2[/math]. Рассмотрим подробнее, почему это будет именно так. Ребро [math]xz[/math] принадлежит паросочетанию [math]M_1[/math], значит вершина [math]y[/math] и какая-то произвольная вершина [math]v[/math] будут покрыты ребром паросочетания [math]M_1[/math], при этом эти ребра не принадлежат паросочетанию [math]M_2[/math], но ребра [math]yt[/math] и [math]vu[/math], где [math]u[/math] — произвольная вершина, принадлежат [math]M_2[/math] и не принадлежат [math]M_1[/math] и так далее. Таким образом и получается чередующийся цикл в графе [math]H[/math]. В силу симметричности [math]x[/math] и [math]z[/math] можно считать, что вершины расположены в порядке [math]tzxy[/math]. Тогда существует путь [math]P_1=t..zx..y[/math] и полное паросочетание в нем, следовательно существует и путь [math]P_2=t..zy..x[/math], содержащий только ребра графа [math]{G'}[/math]. Тогда на пути [math]x..y[/math] возьмем ребра из паросочетания [math]M_2[/math], а на пути [math]t..z[/math] - ребра из паросочетания [math]M_1[/math]. Непокрытыми остались вершины [math]z[/math] и [math]y[/math], которые мы покроем ребром [math]yz[/math]. Вершины, не принадлежащие рассматриваемому циклу, покроем ребрами любого из паросочетаний [math]M_1, M_2[/math] (выберем ребра одного из них). Таким образом, получили полное паросочетание в графе [math]{G'}[/math], противоречие.
В каждом из возможных случаев получили противоречие, значит, наше начальное предположение тоже неверно и [math]{G'} \setminus U[/math] — объединение несвязных полных графов, лемма доказана. |
| [math]\triangleleft[/math] |
Теорема Татта
| Теорема: |
В графе [math]{G}[/math] существует полное паросочетание [math]\Leftrightarrow[/math]
[math]\forall S \subset {V}[/math] выполнено условие: [math]\mathrm{odd}({G} \setminus S) \leqslant \left\vert S \right\vert[/math] (то есть в графе [math]{G}[/math] нет ни одного множества Татта) |
| Доказательство: |
| [math]\triangleright[/math] |
|
[math]\Rightarrow[/math]
Рассмотрим [math]M[/math] — полное паросочетание в графе [math]{G}[/math] и множество вершин [math]S \subset {V}[/math].
Одна из вершин каждой нечетной компоненты связности графа [math] {G} \setminus S[/math] соединена ребром паросочетания [math]M[/math] с какой-то вершиной из [math]S[/math]. Иначе мы не сможем покрыть паросочетанием все вершины этой компоненты связности и получим противоречие с тем, что полное паросочетание существует по условию теоремы. Таким образом, получаем, что [math]\mathrm{odd}({G} \setminus S) \leqslant \left\vert S \right\vert[/math].
[math]\Leftarrow[/math]
Пусть для графа [math]{G}[/math] выполнено, что [math]\mathrm{odd}({G} \setminus S) \leqslant \left\vert S \right\vert[/math], но полного паросочетания в этом графе не существует.
Рассмотрим граф [math]{G'}[/math] и множество вершин [math]U[/math] (из леммы). Так как число нечетных компонент не увеличивается при добавлении новых ребер, то [math]\forall S \subset {V}[/math] выполнено [math]\mathrm{odd}({G'} \setminus S) \leqslant \mathrm{odd}({G} \setminus S) \leqslant \left\vert S \right\vert[/math]. По лемме, доказанной выше: [math]{G'} \setminus U[/math] — объединение несвязных полных графов.
Очевидно, что в каждой четной компоненте связности графа [math]{G'} \setminus U[/math] мы можем построить полное паросочетание. В каждой нечетной компоненте этого графа построим паросочетание, которое покрывает все вершины кроме одной, оставшуюся непокрытой вершину, соединим с какой-то вершиной множества [math]U[/math]. При этом мы будем использовать различные вершины из [math]U[/math], это возможно, так как [math]\mathrm{odd}({G'} \setminus U) \leqslant \left\vert U \right\vert[/math]. Если все вершины множества [math]U[/math] оказались покрытыми, то мы получили полное паросочетание в графе [math]{G'}[/math]. Противоречие, так как по построению в [math]{G'}[/math] нет полного паросочетания.
Значит, в [math]U[/math] осталось какое-то количество непокрытых вершин, при этом их четное число, потому что число вершин в [math]{G'}[/math] четно, так как [math]\mathrm{odd}({G'} \setminus \varnothing) \leqslant \left\vert \varnothing \right\vert = 0[/math] и уже покрыто паросочетанием четное число вершин. Так как в множество [math]U[/math] входят вершины, которые в [math]{G'}[/math] смежны со всеми остальными, то мы сможем разбить оставшиеся вершины на пары и покрыть их паросочетанием.
Таким образом, получили в [math]{G'}[/math] полное паросочетание, что противоречит тому, как мы задали этот граф изначально. Значит, начальное предположение не верно, и в [math]{G}[/math] существует полное паросочетание. |
| [math]\triangleleft[/math] |
См. также
Примечания
Источники информации
