Алгоритм построения базы в пересечении матроидов
| Задача: |
| Даны матроиды и . Необходимо найти максимальное по мощности независимое множество в пересечении и . |
Алгоритм решения
Пусть множество .
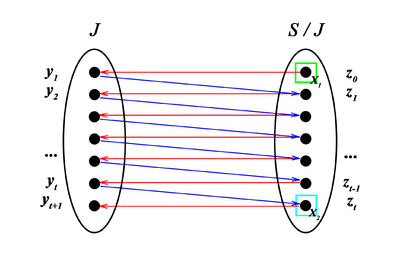
Определим граф замен , где
.
Пусть , , — кратчайший путь из в в графе . может и не существовать.
| Лемма: | ||||||||||
Если в графе нет пути из в , то — искомое максимальное по мощности независимое множество в пересечении и . | ||||||||||
| Доказательство: | ||||||||||
|
Отметим, что если или пустые, то — база в одном из исходных матроидов или и, следовательно, искомое максимальное по мощности независимое множество в пересечении и . Таким образом, предположим, что и непусты. Пусть — множество вершин, из которых достижимы вершины из . Отсутствие пути из в означает, что , и (т.е. в не входит ни одной дуги). Тогда:
| ||||||||||
| Лемма: |
| Доказательство: |
|
Пусть . Тогда и дуги из в составляют единственное полное паросочетание в . То есть, согласно лемме о единственном паросочетании в подграфе замен, . К тому же, , иначе — не кратчайший путь из в . Это означает, что , то есть . Так как (т.е. . Симметрично и, следовательно, . |
Псевдокод
= isMaximal = false while not isMaximal построить граф замен кратчайший путь из в if = else isMaximal = true
Подсказки
- Воспользуйтесь одним массивом для проверки множества на независимость по цветам,
- для проверки ацикличности графа при добавлении ребра можно использовать СНМ или обходом в глубину,
- для нахождения кратчайшего пути можно использовать обход в ширину, первоначально добавив фиктивную вершину, соединив её с вершинами из множества .
Теорема Эдмондса-Лоулера
| Теорема (Эдмондса-Лоулера): |
Пусть , — матроиды. Тогда . Где и — ранговые функции в первом и втором матроиде соответственно. |
| Доказательство: |
|
Докажем неравенство Выберем произвольные , , тогда
и — независимые в обоих матроидах (как подмножества независимового ), значит
Но и , значит
В силу произвольности и получаем
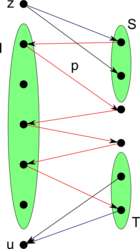
Обозначим , . Если , добавим их пересечение в . Построим граф замен . Добавим вершину , не влияющую на независимость в первом матроиде — из неё будут вести рёбра во все вершины множества . Пусть — кратчайший путь из в , — путь с добавленным в начало ребром из . По лемме о единственном паросочетании и лемме о единственном паросочетании, индуцированном кратчайшем путём . Теперь добавим вершину , не влияющую на независимость во втором матроиде — в неё будут вести рёбра из всех вершин множества . Тогда (путь с добавленным ребром в ) — кратчайший путь из в . Аналогично, . Отсюда следует, что , причём .Будем таким образом увеличивать , пока существует путь . Рассмотрим момент, когда такого пути не нашлось. Введём обозначение: . Докажем, что от противного. Пусть , тогда существует , такое, что . Если , то и из есть путь в . Значит, . Отсюда следует, что существует , такое что . Но тогда ребро имеется в графе, то есть из существует путь в , что противоречит условию . Следовательно, . Аналогично, . Отсюда , то есть при найденных и достигается равенство. Построен пример равенства, значит, теорема доказана. |
См. также
Источники информации
- Chandra Chekuri — Combinatorial Optimization