Точка сочленения, эквивалентные определения — различия между версиями
AReesha (обсуждение | вклад) м (Добавлена теорема) |
|||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 14: | Строка 14: | ||
|proof= | |proof= | ||
| − | <tex>1 \Rightarrow 2</tex> | + | <tex>1 \Rightarrow 2</tex> |
| − | <tex>2 \Rightarrow 1</tex> Пусть <tex>v</tex> принадлежала только одному блоку <tex>C</tex>. Все вершины <tex>u_1...u_n</tex>, смежные с <tex>v</tex>, также лежат в <tex>C</tex> (в силу рефлексивности отношения вершинной двусвязности). Между каждой парой <tex>u_i, u_j</tex> вершин из <tex>u_1...u_n</tex> существует как минимум два вершинно непересекающихся пути. Теперь удалим <tex>v</tex>. Это разрушит путь <tex>u_{i}vu_{j}</tex>, но не разрушит любой оставшийся, так как иначе он тоже прошел бы через <tex>v</tex>. | + | Пусть вершина <tex>v</tex> принадлежит некоторым блокам <tex>A</tex> и <tex>B</tex>. Вершине <tex>v</tex> инцидентны некоторые ребра <tex>e=uv \in A</tex> и <tex>f=wv \in B</tex>. Ребра <tex>e</tex> и <tex>f</tex> находятся в различных блоках, поэтому не существует двух непересекающихся путей между их концами. Учитывая, что один из путей между концами - путь из <tex>v</tex> в эту же вершину, получаем, что любой путь, соединяющий <tex>u</tex> и <tex>w</tex>, пройдет через <tex>v</tex>. При удалении <tex>v</tex> между <tex>u</tex> и <tex>w</tex> не останется путей, и одна из компонент связности распадется на две. |
| + | |||
| + | <tex>2 \Rightarrow 1</tex> | ||
| + | |||
| + | Пусть <tex>v</tex> принадлежала только одному блоку <tex>C</tex>. Все вершины <tex>u_1...u_n</tex>, смежные с <tex>v</tex>, также лежат в <tex>C</tex> (в силу рефлексивности отношения вершинной двусвязности). Между каждой парой <tex>u_i, u_j</tex> вершин из <tex>u_1...u_n</tex> существует как минимум два вершинно непересекающихся пути. Теперь удалим <tex>v</tex>. Это разрушит путь <tex>u_{i}vu_{j}</tex>, но не разрушит любой оставшийся, так как иначе он тоже прошел бы через <tex>v</tex>. | ||
Рассмотрим <tex>D</tex> {{---}} компоненту связности, в которой лежала <tex>v</tex>. Пусть между вершинами <tex>u, w \in D</tex> существовал путь, проходящий через <tex>v</tex>. Но он проходил также через некоторые вершины из <tex>u_1...u_n</tex>, связность которых не нарушилась, поэтому есть как минимум еще один путь, отличный от удаленного. Противоречие: число компонент связности не увеличилось. | Рассмотрим <tex>D</tex> {{---}} компоненту связности, в которой лежала <tex>v</tex>. Пусть между вершинами <tex>u, w \in D</tex> существовал путь, проходящий через <tex>v</tex>. Но он проходил также через некоторые вершины из <tex>u_1...u_n</tex>, связность которых не нарушилась, поэтому есть как минимум еще один путь, отличный от удаленного. Противоречие: число компонент связности не увеличилось. | ||
}} | }} | ||
| Строка 30: | Строка 34: | ||
|proof= | |proof= | ||
<tex>1 \Rightarrow 3</tex> Так как <tex>v</tex> {{---}} точка сочленения графа <tex>G</tex>, то граф <tex>G \setminus v</tex> не связен и имеет по крайней мере две компоненты. Образуем разбиение <tex>V \setminus \{v\}</tex>, отнеся к <tex>U</tex> вершины одной из этих компонент, а к <tex>W</tex> {{---}} вершины всех остальных компонент. Тогда любые две вершины <tex>u \in U</tex> и <tex>w \in W</tex> лежат в разных компонентах графа <tex>G \setminus v</tex>. Следовательно, любой простой путь из <tex>u</tex> в <tex>w</tex> графа <tex>G</tex> содержит <tex>v</tex>. | <tex>1 \Rightarrow 3</tex> Так как <tex>v</tex> {{---}} точка сочленения графа <tex>G</tex>, то граф <tex>G \setminus v</tex> не связен и имеет по крайней мере две компоненты. Образуем разбиение <tex>V \setminus \{v\}</tex>, отнеся к <tex>U</tex> вершины одной из этих компонент, а к <tex>W</tex> {{---}} вершины всех остальных компонент. Тогда любые две вершины <tex>u \in U</tex> и <tex>w \in W</tex> лежат в разных компонентах графа <tex>G \setminus v</tex>. Следовательно, любой простой путь из <tex>u</tex> в <tex>w</tex> графа <tex>G</tex> содержит <tex>v</tex>. | ||
| + | |||
| + | <tex>3 \Rightarrow 2</tex> Следует из того, что (2) - частный случай (3). | ||
| + | |||
| + | <tex>2 \Rightarrow 1</tex> Если <tex>v</tex> принадлежит любому простому пути в <tex>G</tex>, соединяющему <tex>u</tex> и <tex>w</tex>, то в <tex>G</tex> нет простого пути, соединяющего эти вершины в <tex>G \setminus \{v\}</tex>. Поскольку <tex>G \setminus \{v\}</tex> не связен, то <tex>v</tex> {{---}} точка сочленения графа <tex>G</tex>. | ||
| + | }} | ||
| + | |||
| + | |||
| + | {{Теорема | ||
| + | |statement= | ||
| + | Пусть <tex>G</tex> {{---}} связный граф с не менее чем тремя вершинами. Следующие утверждения эквивалентны: | ||
| + | # <tex>G</tex> {{---}} блок ; | ||
| + | # любые две вершины графа <tex>G</tex> принадлежат некоторому общему простому циклу; | ||
| + | # любая вершина и любое ребро графа <tex>G</tex> принадлежат некоторому общему простому циклу; | ||
| + | # любые два ребра графа <tex>G</tex> принадлежат некоторому общему простому циклу; | ||
| + | # для любых двух вершин и любого ребра графа <tex>G</tex> существует простая цепь, соединяющая эти вершины и включающая данное ребро; | ||
| + | # для любых трех различных вершин графа <tex>G</tex> существует простая цепь, соединяющая две из них и проходящая через третью; | ||
| + | # для каждых трех различных вершин графа <tex>G</tex> существует простая цепь, соединяющая две из них и не проходящая через третью. | ||
| + | |||
| + | |proof= | ||
| + | <tex>1 \Rightarrow 2</tex> Пусть <tex>u</tex>,<tex>v</tex> - различные вершины графа <tex>G</tex>, а <tex>U</tex> - множество вершин, отличных от <tex>u</tex>, которые лежат на простом цикле, содержащем <tex>u</tex>. Поскольку в <tex>G</tex> по крайней мере три вершины и нет точек сочленения, то в <tex>G</tex> нет также мостов. Значит, каждая вершина, смежная с <tex>u</tex>, принадлежит <tex>U</tex>, т.е. <tex>U</tex> не пусто. Предположим, что <tex>u</tex> не принадлежит <tex>U</tex>. Пусть <tex>w</tex> - вершина в <tex>U</tex>, для которой расстояние <tex>d</tex>(<tex>w</tex>-<tex>u</tex>)-цепь минимально. Пусть <tex>P_0</tex> - кратчайшая простая (<tex>w</tex>-<tex>u</tex>)- цепь, а <tex>P_1</tex> и <tex>P_2</tex> - две простые (<tex>u</tex>-<tex>w</tex>)-цепи цикла, содержащего <tex>u</tex> и <tex>w</tex>. Так как <tex>w</tex> не является точкой сочленения, то существует простая (<tex>u</tex>-<tex>v</tex>)-цепь <tex>P'</tex>, не содержащая <tex>w</tex>. Обозначим через <tex>w'</tex> ближайшую к <tex>u</tex> вершину, принадлежащую <tex>P'</tex>, которая также принадлежит <tex>P_0</tex>, и через <tex>u'</tex> последнюю вершину (<tex>u</tex>-<tex>w'</tex>)-подцепи в <tex>P'</tex>, которая принадлежит или <tex>P_1</tex>, или <tex>P_2</tex>. Не теряя общности, предположим, что <tex>u</tex>' принадлежит <tex>P_1</tex>. | ||
| + | Пусть <tex>Q_1</tex> - простая (<tex>u</tex>-<tex>w'</tex>)-цепь, содержащая (<tex>u</tex>-<tex>u'</tex>)-подцепь цепи <tex>P_1</tex> и (<tex>u'</tex>-<tex>w'</tex>)-подцепь цепи <tex>P'</tex>, а <tex>Q_2</tex> - простая (<tex>u</tex>-<tex>w'</tex>)-подцепь, содержащая <tex>P_2</tex> вслед за (<tex>w</tex>-<tex>w</tex>')-подцепью цепи <tex>P_0</tex>. Ясно, что <tex>Q_1</tex> и <tex>Q_2</tex> - непересекающиеся простые (<tex>u</tex>-<tex>w'</tex>)-цепи. Вместе они образуют простой цикл, так что <tex>w'</tex> принадлежит <tex>U</tex>. Поскольку <tex>w'</tex> принадлежит кратчайшей цепи, <tex>d</tex>(<tex>w'</tex>,<tex>u</tex>)<<tex>d</tex>(<tex>w</tex>,<tex>u</tex>). Это противоречит выбору <tex>w</tex> и, следовательно, доказывает, что <tex>u</tex> и <tex>v</tex> лежат на одном простом цикле. | ||
<tex>3 \Rightarrow 2</tex> Следует из того, что (2) - частный случай (3). | <tex>3 \Rightarrow 2</tex> Следует из того, что (2) - частный случай (3). | ||
Версия 16:53, 8 мая 2016
| Определение: |
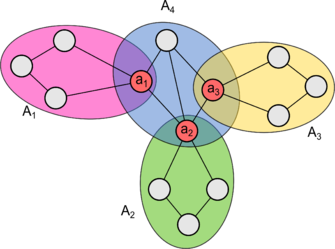
| Точка сочленения графа — вершина, принадлежащая как минимум двум блокам . |
| Определение: |
| Точка сочленения графа — вершина, при удалении которой в увеличивается число компонент связности. |
| Лемма: |
Определения и эквивалентны. |
| Доказательство: |
|
Пусть вершина принадлежит некоторым блокам и . Вершине инцидентны некоторые ребра и . Ребра и находятся в различных блоках, поэтому не существует двух непересекающихся путей между их концами. Учитывая, что один из путей между концами - путь из в эту же вершину, получаем, что любой путь, соединяющий и , пройдет через . При удалении между и не останется путей, и одна из компонент связности распадется на две.
Пусть принадлежала только одному блоку . Все вершины , смежные с , также лежат в (в силу рефлексивности отношения вершинной двусвязности). Между каждой парой вершин из существует как минимум два вершинно непересекающихся пути. Теперь удалим . Это разрушит путь , но не разрушит любой оставшийся, так как иначе он тоже прошел бы через . Рассмотрим — компоненту связности, в которой лежала . Пусть между вершинами существовал путь, проходящий через . Но он проходил также через некоторые вершины из , связность которых не нарушилась, поэтому есть как минимум еще один путь, отличный от удаленного. Противоречие: число компонент связности не увеличилось. |
| Теорема: |
Следующие утверждения эквивалентны:
|
| Доказательство: |
|
Так как — точка сочленения графа , то граф не связен и имеет по крайней мере две компоненты. Образуем разбиение , отнеся к вершины одной из этих компонент, а к — вершины всех остальных компонент. Тогда любые две вершины и лежат в разных компонентах графа . Следовательно, любой простой путь из в графа содержит . Следует из того, что (2) - частный случай (3). Если принадлежит любому простому пути в , соединяющему и , то в нет простого пути, соединяющего эти вершины в . Поскольку не связен, то — точка сочленения графа . |
| Теорема: |
Пусть — связный граф с не менее чем тремя вершинами. Следующие утверждения эквивалентны:
|
| Доказательство: |
|
Пусть , - различные вершины графа , а - множество вершин, отличных от , которые лежат на простом цикле, содержащем . Поскольку в по крайней мере три вершины и нет точек сочленения, то в нет также мостов. Значит, каждая вершина, смежная с , принадлежит , т.е. не пусто. Предположим, что не принадлежит . Пусть - вершина в , для которой расстояние (-)-цепь минимально. Пусть - кратчайшая простая (-)- цепь, а и - две простые (-)-цепи цикла, содержащего и . Так как не является точкой сочленения, то существует простая (-)-цепь , не содержащая . Обозначим через ближайшую к вершину, принадлежащую , которая также принадлежит , и через последнюю вершину (-)-подцепи в , которая принадлежит или , или . Не теряя общности, предположим, что ' принадлежит . Пусть - простая (-)-цепь, содержащая (-)-подцепь цепи и (-)-подцепь цепи , а - простая (-)-подцепь, содержащая вслед за (-')-подцепью цепи . Ясно, что и - непересекающиеся простые (-)-цепи. Вместе они образуют простой цикл, так что принадлежит . Поскольку принадлежит кратчайшей цепи, (,)<(,). Это противоречит выбору и, следовательно, доказывает, что и лежат на одном простом цикле. Следует из того, что (2) - частный случай (3). Если принадлежит любому простому пути в , соединяющему и , то в нет простого пути, соединяющего эти вершины в . Поскольку не связен, то — точка сочленения графа . |
Источники информации
- Харари, Ф. Теория графов. — М.: Книжный дом «ЛИБРОКОМ», 2009