Трапецоидная карта — различия между версиями
Komarov (обсуждение | вклад) |
Komarov (обсуждение | вклад) (→Асимптотика) |
||
| Строка 176: | Строка 176: | ||
==Асимптотика== | ==Асимптотика== | ||
===Запрос=== | ===Запрос=== | ||
| − | Предположим у нас есть запрос на локализацию точки q. Время затраченное на этот запрос будет линейно зависеть от глубина графа. | + | Предположим у нас есть запрос на локализацию точки <tex>q</tex>. Время, затраченное, на этот запрос будет линейно зависеть от глубина графа. |
| − | При добавлении в карту очередного отрезка(в дальнейшем итерация алгоритма) глубина графа увеличивается максимум на 3. Из этого мы можем сделать простую оценку. | + | При добавлении в карту очередного отрезка(в дальнейшем, итерация алгоритма), глубина графа увеличивается максимум на 3. Из этого мы можем сделать простую оценку. |
Наибольшее время на запрос, которое мы можем потратить {{---}} <tex>3n</tex>. Произойдет это в самом ужасном из самых ужасных случаев. | Наибольшее время на запрос, которое мы можем потратить {{---}} <tex>3n</tex>. Произойдет это в самом ужасном из самых ужасных случаев. | ||
| − | Как говорилось раньше отрезки мы добавляем | + | Как говорилось раньше, отрезки мы добавляем в случайном порядке, а потому, редко будет самый ужасный случай и, с вероятностных точек зрения, время на запрос будет меньше. |
| − | Рассмотрим путь пройденный точкой по графу. Каждый узел был создан на какой-то итерации цикла. Обозначим за <tex>X_i</tex> | + | Рассмотрим путь, пройденный точкой по графу. Каждый узел был создан на какой-то итерации цикла. Обозначим за <tex>X_i</tex> количество узлов, созданных на итерации <tex>i</tex>. |
| − | Так как никто не выбирал исходное множество отрезков и запрос q, <tex>X_i</tex> - рандомная величина зависящая только от рандомного порядка добавления отрезков. | + | Так как никто не выбирал исходное множество отрезков и запрос <tex>q</tex>, <tex>X_i</tex> {{---}} рандомная величина, зависящая только от рандомного порядка добавления отрезков. |
<tex>E[\sum^{n}_{i=1}X_i] = \sum^{n}_{i=1}E[X_i]</tex> | <tex>E[\sum^{n}_{i=1}X_i] = \sum^{n}_{i=1}E[X_i]</tex> | ||
| − | Как уже упоминалось на каждой итерации добавляется не более 3 узлов, а значит <tex>X_i</tex> | + | Как уже упоминалось, на каждой итерации добавляется не более 3 узлов, а значит <tex>X_i \leq 3</tex>. |
| − | Считая, что <tex> P_i </tex> - вероятность того, что существует узел, который встречается при нашем запросе созданный на i-ой итерации. | + | Считая, что <tex>P_i</tex> {{---}} вероятность того, что существует узел, который встречается при нашем запросе, созданный на <tex>i</tex>-ой итерации. |
<tex>\sum^{n}_{i=1}E[X_i] <= \sum^{n}_{i=1}3P_i</tex> | <tex>\sum^{n}_{i=1}E[X_i] <= \sum^{n}_{i=1}3P_i</tex> | ||
| Строка 198: | Строка 198: | ||
Начинаем оценивать <tex> P_i </tex>. | Начинаем оценивать <tex> P_i </tex>. | ||
| − | Что значит, что узел был создан на i-ой итерации и встретился при запросе q? | + | Что значит, что узел был создан на <tex>i</tex>-ой итерации и встретился при запросе <tex>q</tex>? |
| − | Это значит, что на i - 1-ой итерации мы локализовывали q в трапецоиде <tex> \Delta_q(i - 1) </tex>, | + | Это значит, что на <tex>i-1</tex>-ой итерации мы локализовывали <tex>q</tex> в трапецоиде <tex>\Delta_q(i-1)</tex>,а на <tex>i</tex>-ой итерации уже в трапецоиде <tex> \Delta_q(i) </tex> и эти два трапецоида разные. |
| − | |||
| − | а на i-ой итерации уже в трапецоиде <tex> \Delta_q(i) </tex> и эти два трапецоида разные. | ||
То есть, после добавления непонятно чего в карту, трапецоид изменился. | То есть, после добавления непонятно чего в карту, трапецоид изменился. | ||
| − | Таким образом <tex>P_i | + | Таким образом <tex>P_i = P(\Delta_q(i) \ne \Delta_q(i - 1))</tex>. |
| − | Если эти два трапеецоида не равны, значит на i-ой итерации трапецоид <tex> \Delta_q(i) </tex> был одним из созданных при модификации. | + | Если эти два трапеецоида не равны, значит на i-ой итерации трапецоид <tex>\Delta_q(i)</tex> был одним из созданных при модификации. |
| − | Заметим, что все трапецоиды созданные на этой итерации были смежны текущему отрезку(<tex> s_i </tex>). | + | Заметим, что все трапецоиды, созданные на этой итерации, были смежны текущему отрезку(<tex>s_i</tex>). |
| − | Значит либо <tex> s_i | + | Значит либо <tex>s_i = \operatorname{top} \Delta_i</tex> или <tex>\operatorname{bottom} \Delta_i</tex>, либо концы <tex>s_i = \operatorname{leftp} \Delta_i</tex> или <tex>\operatorname{rightp} \Delta_i</tex>. |
| − | Зафиксируем множество отрезков на i-ой итерации. Тогда состояние трапецоидов никак не будет зависеть от порядка добавленных отрезков. | + | Зафиксируем множество отрезков на <tex>i</tex>-ой итерации. Тогда состояние трапецоидов никак не будет зависеть от порядка добавленных отрезков. |
| − | Тогда, вероятность изменения трапецоида - это его вероятность исчезнуть если удалится <tex>s_i</tex>. | + | Тогда, вероятность изменения трапецоида {{---}} это его вероятность исчезнуть, если удалится <tex>s_i</tex>. |
| − | Тогда переходим, к | + | Тогда переходим, к <tex>\operatorname{top} \Delta_i</tex> и т.п. так как мы уже говорили, что <tex>s_i</tex> будет определенной стороной при навигации. |
| − | Отрезки добавлялись рандомно поэтому в качестве <tex>s_i</tex> мог быть любой отрезок из <tex>S_i</tex>. А тогда вероятность для всех сторон | + | Отрезки добавлялись рандомно, поэтому, в качестве <tex>s_i</tex> мог быть любой отрезок из <tex>S_i</tex>. А, тогда, вероятность для всех сторон <tex>\frac1i</tex>. |
Суммируем по всем 4 сторонам. | Суммируем по всем 4 сторонам. | ||
| − | Таким образом <tex>P_i = P( \Delta_q(i) \ne \Delta_q(i - 1)) = P( \Delta_q(i) \in \Delta_q(i - 1) ) \le | + | Таким образом <tex>P_i = P( \Delta_q(i) \ne \Delta_q(i - 1)) = P( \Delta_q(i) \in \Delta_q(i - 1) ) \le \frac4i</tex> |
| − | <tex>\sum^{n}_{i=1}E[X_i] \le \sum^{n}_{i=1}3P_i \le \sum^{n}_{i=1}12 | + | <tex>\sum^{n}_{i=1}E[X_i] \le \sum^{n}_{i=1}3P_i \le \sum^{n}_{i=1}\frac{12}i \le 12\sum^{n}_{i=1}(1/i) \approx 12 \cdot log(n)</tex> |
===Память=== | ===Память=== | ||
| − | Заметим, что количество трапецоидов как мы доказали раньше равно O(n), поэтому мы должны оценить количество узлов созданых на i-ой итерации. | + | Заметим, что количество трапецоидов, как мы доказали раньше, равно <tex>\mathcal{O}(n)</tex>, поэтому мы должны оценить количество узлов созданых на <tex>i</tex>-ой итерации. |
А результирующее выражение для памяти тогда будет | А результирующее выражение для памяти тогда будет | ||
| − | + | <tex>\mathrm{Mem} = \mathcal{O}(n) + \sum^{n}_{i=1}</tex> количество узлов созданное на <tex>i</tex>-ой итерации | |
| − | Обозначив за k_i количество узлов созданное на i-ой итерации | + | Обозначив за <tex>k_i</tex> количество узлов, созданное на <tex>i</tex>-ой итерации |
| − | + | <tex>\mathrm{Mem} = \mathcal{O}(n) + \sum^{n}_{i=1} E[k_i]</tex> | |
| − | Используя вывод из предыдущей части получаем, что <tex>E[k_i] \le O(i) | + | Используя вывод из предыдущей части получаем, что <tex>E[k_i] \le \frac{\mathcal{O}(i)}i = \mathcal{O}(1)</tex> |
| − | А тогда | + | А тогда <tex>\mathrm{Mem} = \mathcal{O}(n)</tex> |
| − | Из этих двух выводов очевидно следует, что время построения карты равно <tex>O( | + | Из этих двух выводов очевидно следует, что время построения карты равно <tex>\mathcal{O}(n \log n)</tex>. |
==Реализация== | ==Реализация== | ||
Версия 01:24, 11 марта 2012
Трапецоидная карта — геометрическая структура позволяющая локализоваться на площади за .
Содержание
Постановка задачи
Предположим, у нас есть наши координаты, и есть карта мира.
Мы можем найти по карте наше местоположение и сказать в какой стране мы находимся. Области задаются замкнутыми ломаными.
Формальная постановка задачи
Есть множество отрезков на плоскости. Есть запрос (точка ), на выходе — область, в которой находится точка .
Структура данных
- Геометрическая
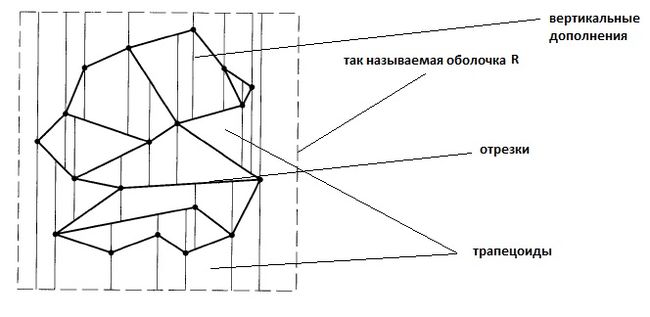
У нас есть множество отрезков, ограниченных оболочкой (это не выпуклая оболочка, а просто мнимая граница плоскости, за которую не вылезают отрезки).
Мы договариваемся, что никакие две точки не лежат на одной вертикали(в противном случае всё ещё противнее).
Трапецоидная карта множества отрезков — это эти отрезки и из каждой точки выпущены два луча — вверх и вниз, до первого пересечения с другим отрезком или с оболочкой .
| Лемма: |
Любой трапецоидной карты ограничен одним или двумя вертикальными отрезками и обязательно двумя не вертикальными отрезками. |
Именно отсюда берется название структуры, так как любой либо трапеция, либо треугольник.
Введем обозначения для навигации по карте.
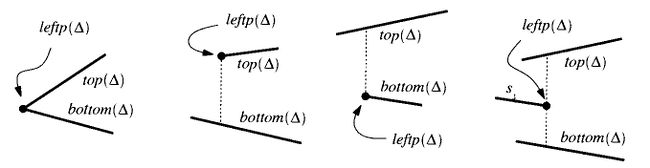
- левая граница () — точка, определяющая левую сторону трапецоида или, в случаи треугольника, просто являющаяся левой вершиной.
- правая граница () — аналогично левой, только справа.
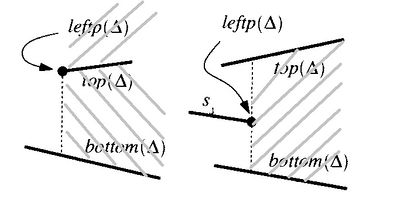
- верхний отрезок () и нижний отрезок() — отрезки, ограничивающие, трапецоид сверху и снизу.
- трапецоиды называются смежными, если имеют общую вертикальную границу.
- пусть и смежны и либо , либо . Тогда и называют либо нижними, либо верхними левыми соседями.
| Теорема: |
Трапецоидная карта, построенная на отрезках содержит максимум вершины и максимум трапецоид. |
| Доказательство: |
Будем смотреть на левую сторону трапецоида. У каждого трапецоида есть точка . Либо это конец какого-то отрезка, либо это левый нижний угол оболочки. При этом можно сразу сказать, что левый и нижний угол будут соответствовать только одному трапецоиду. Далее заметим, что правый конец отрезка может быть только для одного трапецоида. Левый конец может быть максимум для двух трапецоидов. Из этого следует, что количество трапецоидов . |
Хранить трапецоиды можно в чем угодно. Вместе с самим трапецоидом, стоит хранить , , и . Так же следует хранить соседей трапецоида.
- Поисковая структура
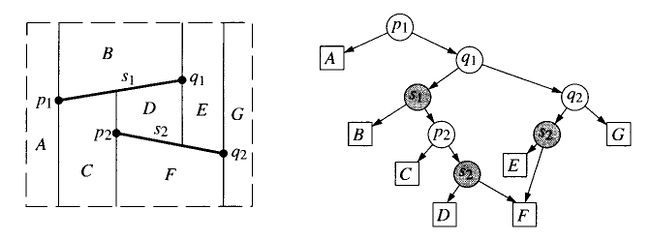
Поисковая структура представляет из себя ациклический граф с одним корнем и соответствующими трапецоидам листьями.
У каждого узла есть два ребенка. При этом узел может быть двух типов.
- Первый тип узла - точка, соответствующая концу отрезка.
- Второй тип узла - отрезок.
Во время запроса мы двигаемся по графу от его корня до момента, когда окажемся в листе. Это и будет означать, что точка находится внутри трапецоида.
Если мы находимся не в листе, то мы должны опредетиться, в каком из детей мы окажемся дальше.
Еcть два правила:
- Если текущий узел соответсвует вершине, то смотрим левее или правее мы находимся(проверка по -координате).
- Если текущий узел соответствует отрезку, то смотрим выше или ниже мы находимся(проверка по -координате).
- Плохие случаи:
Мы находимся на одной вертикали с вершиной
Мы находимся на отрезке
(Решение: молиться, или просто обрабатывать вручную.)
Алгоритм
Во время построения трапецоидной карты(в дальнейшем ) алгоритм так же строит структуру для поиска.
Так как трапецоидная карта — геометрическая структура, а основные операции ведутся именно с поисковой, основной упор делается на неё.
Наш алгоритм добавляет отрезки по одному и, после каждого добавления, модидицирует и .
Порядок добавления отрезков
От порядка добавления зависит время запроса. Как? Время запрос пропорцианально глубине графа.
Считается, что если добавлять отрезки в случайном порядке, то время будет хорошим. Почему и какое время будет достигаться, расписано дальше.
Алгоритм
- Добавили отрезок.
- Нашли все трапецоиды, которые пересек новый отрезок.
- Удалили их.
- Создали новые трапецоиды.
Поиск трапецоидов, которые пересек отрезок
Чтобы модифицировать карту, мы должны понять, где произошло изменение.
Оно произошло в тех трапецоидах, которые пересек текущий отрезок, или можно сказать, что трапецоид с -ой итерации не будет в -ой только если его пересек отрезок.
Пусть якобы есть множество трапецоидов , упорядоченное по
Пусть — один из правых соседей . Так же, при этом не сложно понять, каким соседом он является.
Если лежит выше , то сосед нижний и наоборот.
Это значит, что, если мы знаем первый трапецоид, то мы можем найти остальные просто обходя по карте соседей справа.
Чтобы найти первый трапецоид, нужно просто локализовать правый конец в текущей карте.
update
Рассмотрим подробнее последние две части
Есть два случая.
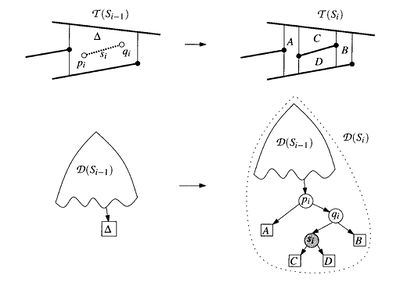
- Простой — отрезок не пересекает ни одного трапецоида, то есть целиком внутри.
Тогда удаляем этот старый трапецоид и на его место ставим дерево из двух концов отрезка, отрезка и четырех образовавшихся трапецоидов.
Важно не забыть правильно определить соседей новых трапецоидов.
В случае, если какие-то трапецоиды выродятся в треугольники, будет не четыре новых трапецоида, а 2 или 3. Слава богу это не самая большая проблема.
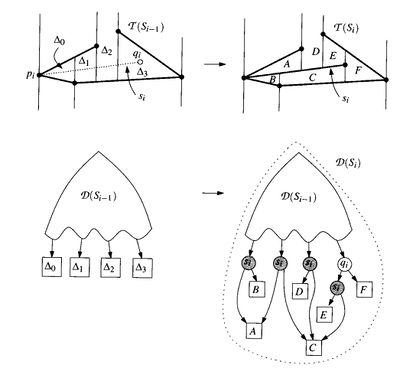
- Сложный — отрезок пересекает сразу несколько трапецоидов.
Итак наш отрезок пересекает трапецоиды .
Сначала добавляем вертикальные лучи из концов текущего отрезка. Это нужно, чтобы модифицировать и . Теперь мы должны удалить соответствующие листья и на их место поставить те новые, которые появились из-за изменения лучей.
Дальше мы модифицуруем вертикальные лучи, которые пересекают текущий отрезок. Этот процесс происходит достаточно быстро, так мы храним много информацию об этих лучах.
По-хорошему, то, как это происходит, просто ужасно и видеть этого не хочется. А все потому, что много что добавляет много новых узлов.
.
Случай коллизии
Рассмотрим момент, когда мы мы строим карты. Мы должны добавить очередной отрезок.
Предположим, левый конец отрезка лежит на одной вертикале с уже добавленной в карту точкой .
Скажем, что наша точка лежит правее, чем та, которая уже есть. В случае, если мы попали на уже созданный отрезок, мы скажем, что находимся, например, ниже его.
Что при этом произойдет.
- С геометрической точки зрения, появится ещё несколько трапецоидов, как в случае, если бы вновь добавленная точка была правее на .
А значит, у трапецоида по прежнему не более двух правых соседей.
- С точки зрения поисковой структуры мы по-прежнему можем локализоваться. По крайней мере, узел, соответствующий точке будет иметь правым сыном нашу точку.
Итого, слова "трапецоидные карты просты отсутствие случаев" появляются именно отсюда, так как, казалось бы, неприятный случай будет прописан заменой на
Асимптотика
Запрос
Предположим у нас есть запрос на локализацию точки . Время, затраченное, на этот запрос будет линейно зависеть от глубина графа.
При добавлении в карту очередного отрезка(в дальнейшем, итерация алгоритма), глубина графа увеличивается максимум на 3. Из этого мы можем сделать простую оценку.
Наибольшее время на запрос, которое мы можем потратить — . Произойдет это в самом ужасном из самых ужасных случаев.
Как говорилось раньше, отрезки мы добавляем в случайном порядке, а потому, редко будет самый ужасный случай и, с вероятностных точек зрения, время на запрос будет меньше.
Рассмотрим путь, пройденный точкой по графу. Каждый узел был создан на какой-то итерации цикла. Обозначим за количество узлов, созданных на итерации .
Так как никто не выбирал исходное множество отрезков и запрос , — рандомная величина, зависящая только от рандомного порядка добавления отрезков.
Как уже упоминалось, на каждой итерации добавляется не более 3 узлов, а значит .
Считая, что — вероятность того, что существует узел, который встречается при нашем запросе, созданный на -ой итерации.
Начинаем оценивать .
Что значит, что узел был создан на -ой итерации и встретился при запросе ?
Это значит, что на -ой итерации мы локализовывали в трапецоиде ,а на -ой итерации уже в трапецоиде и эти два трапецоида разные.
То есть, после добавления непонятно чего в карту, трапецоид изменился.
Таким образом .
Если эти два трапеецоида не равны, значит на i-ой итерации трапецоид был одним из созданных при модификации.
Заметим, что все трапецоиды, созданные на этой итерации, были смежны текущему отрезку().
Значит либо или , либо концы или .
Зафиксируем множество отрезков на -ой итерации. Тогда состояние трапецоидов никак не будет зависеть от порядка добавленных отрезков.
Тогда, вероятность изменения трапецоида — это его вероятность исчезнуть, если удалится .
Тогда переходим, к и т.п. так как мы уже говорили, что будет определенной стороной при навигации.
Отрезки добавлялись рандомно, поэтому, в качестве мог быть любой отрезок из . А, тогда, вероятность для всех сторон .
Суммируем по всем 4 сторонам.
Таким образом
Память
Заметим, что количество трапецоидов, как мы доказали раньше, равно , поэтому мы должны оценить количество узлов созданых на -ой итерации.
А результирующее выражение для памяти тогда будет
количество узлов созданное на -ой итерации
Обозначив за количество узлов, созданное на -ой итерации
Используя вывод из предыдущей части получаем, что
А тогда
Из этих двух выводов очевидно следует, что время построения карты равно .
Реализация
Здесь будут рассмотрены некоторые основные моменты реализации Это только идейные реализации в коде все выглядет пример в 50 раз хуже.(по количеству строк)
Класс "трапецоид"
struct Trapezoid
Trapezoid next Trapezoid up Trapezoid down Trapezoid end Segment top Segment bottom Point left Point right
Построение трапецоидной карты
TrapezoidMap(S - segments)
Строим оболочку(просто находим крайние точки множества отрезков по четырем направлениям)
Строим рандомную перестановку отрезков
for для всех
ищем множество трапецоидов пересекаемых отрезком . //это специальная функция//
Удаляем это множество из карты и добавляем новые узлы появившиеся из-за в поисковой структуре
Аналогично для просто карты
Поиск трапецоидов, которых пересекает отрезок
LookforTrapezoid( - segment)
Запоминаем левый и правый конец Делаем запрос на левый конец в карте. j 0; while q правый от rightp(трапецоид_j) do if rightp(трапецоид_j) над then ставим трапецоид_(j+1) нижним правым соседом трапецоид_j. else ставим трапецоид_(j+1) верхним правым соседом трапецоид_j. j j+1