Участник:Kabanov — различия между версиями
Kabanov (обсуждение | вклад) м |
Kabanov (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | == | + | === Монотонный метод === |
| − | |||
| − | |||
| − | + | {{Определение | |
| + | |id=def_monotone_polygon | ||
| + | |definition= | ||
| + | Простой многоугольник <tex>P</tex> называется '''монотонным''' относительно прямой <tex>l</tex>, если любая <tex>l'</tex>, такая что <tex>l' \perp l</tex>, пересекает стороны <tex>P</tex> не более двух раз (результатом пересечения <tex>l'</tex> и <tex>P</tex> может быть только один отрезок или точка). | ||
| + | }} | ||
| − | + | {{Определение | |
| − | + | |definition= | |
| + | Многоугольник, монотонный относительно <tex>y</tex>-оси называется '''<tex>y</tex>-монотонным'''. | ||
| + | }} | ||
| − | |||
| − | + | Суть данного метода заключается в том, чтобы разбить многоугольник на монотонные части, а затем триангулировать каждую из них. | |
| + | === Разбиение многоугольника на монотонные части ==== | ||
| + | [[Файл:Split-merge.png|500px|thumb||Пять типов вершин]] | ||
| − | == | + | Рассмотрим самую верхнюю — максимальную по координате <tex>y</tex> вершину. Будем идти вниз по рёбрам до самой нижней — соотвественно минимальной по <tex>y</tex> вершине, то есть таким образом, что для некоторой вершины <tex>j</tex>: <tex>y_j > y_{j+1}</tex>. '''Поворотной''' назовём вершину <tex>i</tex>, на которой направление обхода будет меняется: <tex>y_{i-1} > y_i</tex> и <tex>y_i < y_{i+1}</tex>. Опишем более подробно этот тип вершин. |
| − | + | Уточним понятния ''выше'' и ''ниже'': точка <tex>p</tex> лежит ''ниже'' точки <tex>q</tex>, если <tex>p_y < q_y</tex> или если <tex>p_y = q_y</tex> и <tex>p_x > q_x</tex>, соответственно точка <tex>p</tex> лежит ''выше'' точки <tex>q</tex>, если <tex>p_y > q_y</tex> или если <tex>p_y = q_y</tex> и <tex>p_x < q_x</tex>. Это было сделано для того, чтобы избежать неопределённых ситуаций с вершинами, у которых <tex>y</tex>-координаты равны. | |
| − | + | Обозначим за <tex>\phi</tex> внутренний угол при некоторой вершине и определим далее пять типов вершин, четыре из которых являются поворотными: | |
| − | + | * '''''start вершина''''' — два её соседа лежат ниже её самой и <tex> \phi < \pi </tex> | |
| + | * '''''split вершина''''' — два её соседа лежат ниже её самой и <tex> \phi > \pi </tex> | ||
| + | * '''''end вершина''''' — два её соседа лежат выше её самой и <tex> \phi < \pi </tex> | ||
| + | * '''''merge вершина''''' — два её соседа лежат выше её самой и <tex> \phi > \pi </tex> | ||
| + | * '''''regular вершина''''' — не является поворотной, в отличие от остальных, другими словами один её сосед находится выше, а другой ниже её самой. | ||
| − | = | + | {{Лемма |
| − | + | |statement= | |
| + | Многоугольник <tex>P</tex> является <tex>y</tex>-монотонным, если в нём отсутствуют split и merge вершины. | ||
| + | |proof= | ||
| + | Предположим, что <tex>P</tex> не <tex>y</tex>-монотонный. Тогда докажем, что <tex>P</tex> содержит split и merge вершины. Поскольку <tex>P</tex> не <tex>y</tex>-монотонный, существует горизонтальная прямая <tex>l</tex>, которая пересекает его стороны более двух раз. Выберем <tex>l</tex> таким образом, чтобы самой левой компонентой пересечения <tex>l</tex> и <tex>P</tex> был бы отрезок <tex>pq</tex>. Далее будем двигаться наверх по сторонам <tex>P</tex>, начиная от точки <tex>q</tex>. В результате в некоторой точке <tex>r</tex>, где <tex>r \neq p</tex> (случай '''(a)''' на рисунке), прямая <tex>l</tex> снова пересечёт одну из сторон <tex>P</tex>. Отсюда самая высокая точка, которую мы достигли во время движения по сторонам <tex>P</tex>, будет split вершиной. | ||
| + | |||
| + | [[Файл:Proof_lemma.jpg|450px]] | ||
| + | |||
| + | Если же <tex>r = p</tex> (случай '''(b)''' на рисунке), начём опять двигаться по сторонам <tex>P</tex> теперь уже вниз. Как и в предыдущем случае найдётся некоторая точка <tex>r'</tex>, которая будет результатом пересечения <tex>l</tex> и <tex>P</tex>. При этом <tex>r' \neq p</tex>, в противном случае <tex>l</tex> будет пересекать <tex>P</tex> только два раза, что противоречит выбору <tex>l</tex>. Аналогично предыдущему случаю, выберем теперь самую низкую точку, которую мы достигли во время движения по сторонам P. Она будет merge вершиной. | ||
| + | }} | ||
| − | + | === Алгоритм === | |
| − | === | + | Чтобы сделать многоугольник монотонным, нужно избавиться от split и merge вершин путём проведения непересекающихся дигоналей из таких вершин. |
| − | |||
| − | |||
| − | + | Рассмотрим горизонтальную заметающую прямую <tex>l</tex>, будем перемещать её сверху вниз вдоль плоскости на которой лежит исходный многоугольник <tex>P</tex>. Будем останавливать её в каждой вершине многоугольника. В тот момент, когда на пути заметающей прямой встречается split или merge вершина её нужно соединить с вершиной, у которой расстояние до <tex>l</tex> минимально, при этом она должна лежать соответственно выше или ниже <tex>l</tex>. | |
| − | < | + | [[Файл:Split_case.jpg|200px|thumb|right|Обработка ''split'' вершины <tex>v_i</tex>]] Рассмотрим каждый случай подробнее: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # '''''Split вершина'''''. Пусть <tex>e_j</tex> и <tex>e_k</tex> — ближайшее левое и правое ребро относительно split вершины <tex>v_i</tex>, которые <tex>l</tex> пересекает в данный момент. Нам нужно найти вершину, лежащую между <tex>e_j</tex> и <tex>e_k</tex>, наиболее приближённую к <tex>l</tex>, либо если такой точки не существет выбрать минимальную из верхних вершин <tex>e_j</tex> и <tex>e_k</tex>. Для этого будем хранить указатель на искомую вершину у левого ребра <tex>e_j</tex>, который можно заранее вычислить. Тип вершины, хранящийся в <tex>helper</tex> не имеет значения. Таким образом, чтобы построить диагональ для split вершины нужно обратиться к указателю <tex>helper(e_j)</tex> её левого ребра, которое <tex>l</tex> пересекает в данный момент. | |
| − | + | # '''''Merge вершина'''''. В отличие от случая со split вершиной заранее вычислить указатель <tex>helper</tex> нельзя, поскольку merge вершина <tex>v_i</tex> должна быть соединена с вершиной, лежащей ниже заметающей прямой <tex>l</tex>. Для этого в <tex>helper(e_j)</tex> - левого относительно <tex>v_i</tex> ребра запишем саму <tex>v_i</tex>. Далее спускаем заметающую прямую вниз к следующей вершине <tex>v_m</tex>, обращаемся к <tex>helper</tex>'у её левого ребра. Проверяем, если там хранится merge вершина, строим диагональ <tex>v_{i}v_{m}</tex>. Последняя проверка осуществляется для любого типа вершины, кроме split, согласно п.1. | |
| − | + | [[Файл:Merge_case_1_2.jpg|500px|thumb|center|Обработка ''merge'' вершины <tex>v_i</tex>. На рисунке слева <tex>v_i</tex> записывается в качестве <tex>helper</tex>'а своего левого ребра. На правом рисунке ближайшая вершина <tex>v_m</tex> при обращении к своему левому ребру <tex>helper(e_j)</tex> находит <tex>v_i</tex> и образует диагональ <tex>v_{i}v_m</tex>]] | |
| − | |||
| − | + | === Структуры данных === | |
| + | В подходе, описанном выше, требуется находить пересечения заметающей прямой и левых ребёр многоугольника. Создадим двоичное дерево поиска <tex>T</tex>, в листьях которого будем хранить рёбра, пересекающие <tex>l</tex>, такие, что внутренняя область многоугольника будет лежать справа от них самих. С каждым таким ребром будем хранить его <tex>helper</tex>. Порядок следования листьев в дереве соответствует порядку следования рёбер в многоугольнике: слева направо. Дерево изменяется в зависимости от текущего состояния заметающей прямой. Создадим приоритетную очередь <tex>Q</tex> из вершин, в которой приоритетом будет <tex>y</tex>-координата вершины. Если две вершины имеют одинаковые <tex>y</tex>-координаты, больший приоритет у левой. Вершины будут добавляться на "остановках" заметающей прямой. | ||
| − | + | Многоугольник <tex>P</tex> и добавленные в процессе диагонали удобно хранить в виде списка <tex>D</tex> рёбер с двойными связями (''DCEL — doubly-connected edge list''), так как потом это обеспечит эффективный доступ к каждой из частей, которые нужно будет триангулировать. | |
| − | |||
| − | |||
| − | < | ||
| − | ''' | + | === Псевдокод === |
| + | MakeMonotone(P) | ||
| + | Construct(D); | ||
| + | Construct(Q); // функция Construct создаёт объекты <tex>D</tex> и <tex>Q</tex> , описанные выше. | ||
| + | bst T = new bst(); | ||
| + | while Q <tex> \neq \varnothing </tex> | ||
| + | Remove <tex>v_{max}</tex> from Q // удаление вершины с наивысшим приоритетом из <tex>Q</tex> | ||
| + | switch (Type_of_vertex(<tex>v_{max}</tex>)): // определение типа вершины | ||
| + | case 'start': | ||
| + | HandleStartVertex(<tex>v_{max}</tex>); | ||
| + | case 'end': | ||
| + | HandleEndVertex(<tex>v_{max}</tex>); | ||
| + | case 'split': | ||
| + | HandleSplitVertex(<tex>v_{max}</tex>); | ||
| + | case 'merge': | ||
| + | HandleMergeVertex(<tex>v_{max}</tex>); | ||
| + | case 'regular': | ||
| + | HandleRegularVertex(<tex>v_{max}</tex>); | ||
| − | + | [[Файл:Split-merge - result.png|470px|thumb|right]] | |
| − | |||
| − | + | Опишем теперь каждый метод из последнего switch: | |
| − | |||
| − | |||
| − | + | HandleStartVertex(<tex>v_{i}</tex>) | |
| − | {{ | + | Insert <tex>e_{i}</tex> in T |
| − | + | <tex>helper(e_{i}) \leftarrow v_i</tex> | |
| − | + | ||
| + | HandleSplitVertex(<tex>v_{i}</tex>) | ||
| + | edge <tex>e_j</tex> = <tex>l \cap P</tex> | ||
| + | Search <tex>e_j</tex> in T | ||
| + | Insert edge(<tex>v_{i}</tex>, <tex>helper(e_{j})</tex>) in D | ||
| + | <tex>helper(e_{j}) \leftarrow v_i</tex> | ||
| + | Insert <tex>e_{i}</tex> in T | ||
| + | <tex>helper(e_{i}) \leftarrow v_i</tex> | ||
| + | |||
| + | В последующих трех функциях обработки вершины <tex>v_i</tex> происходит обращение к смежному ребру <tex>e_{i-1}</tex>. Это сделано для вершин, относительно которых внутренняя область <tex>P</tex> лежит справа от них самих (вершина <tex>v_6</tex>), либо для двух подряд идущих merge вершин, таких как <tex>v_2</tex> и <tex>v_8</tex>. | ||
| + | |||
| + | HandleEndVertex(<tex>v_{i}</tex>) | ||
| + | if (Type_of_vertex(<tex>helper(e_{i-1})</tex> = 'merge') | ||
| + | Insert edge(<tex>v_{i}</tex>, <tex>helper(e_{i-1})</tex>) in D | ||
| + | Delete <tex>e_{i-1}</tex> from T | ||
| + | |||
| + | HandleMergeVertex(<tex>v_{i}</tex>) | ||
| + | if (Type_of_vertex(<tex>helper(e_{i-1})</tex> = 'merge') | ||
| + | Insert edge(<tex>v_{i}</tex>, <tex>helper(e_{i-1})</tex>) in D | ||
| + | Delete <tex>e_{i-1}</tex> from T | ||
| + | edge <tex>e_j</tex> = <tex>l \cap P</tex> | ||
| + | Search <tex>e_j</tex> in T | ||
| + | if (Type_of_vertex(<tex>helper(e_{j})</tex> = 'merge') | ||
| + | Insert edge(<tex>v_{i}</tex>, <tex>helper(e_{j})</tex>) in D | ||
| + | <tex>helper(e_{j}) \leftarrow v_i</tex> | ||
| + | |||
| + | HandleRegularVertex(<tex>v_{i}</tex>) | ||
| + | if (interior of <tex>P</tex> lies to the right of <tex>v_{i}</tex>) | ||
| + | then | ||
| + | if (Type_of_vertex(<tex>helper(e_{i-1})</tex> = 'merge') | ||
| + | Insert edge(<tex>v_{i}</tex>, <tex>helper(e_{i-1})</tex>) in D | ||
| + | Delete <tex>e_{i-1}</tex> from T | ||
| + | Insert <tex>e_{i}</tex> in T | ||
| + | <tex>helper(e_{i}) \leftarrow v_i</tex> | ||
| + | else | ||
| + | edge <tex>e_j</tex> = <tex>l \cap P</tex> | ||
| + | Search <tex>e_j</tex> in T | ||
| + | if (Type_of_vertex(<tex>helper(e_{j})</tex> = 'merge') | ||
| + | Insert edge(<tex>v_{i}</tex>, <tex>helper(e_{j})</tex>) in D | ||
| + | <tex>helper(e_{j}) \leftarrow v_i</tex> | ||
| + | ===== Корректность ===== | ||
| + | {{Лемма | ||
|statement= | |statement= | ||
| − | + | Функция ''MakeMonotone(P)'' корректно выполняет разбиение многоугольника <tex>P</tex>. Другими словами эта функция добавляет в <tex>P</tex> множество непересекающихся диагоналей, которые разбивают <tex>P</tex> на монотонные части. | |
| − | |proof= | + | |proof=Тот факт, что <tex>P</tex> разбивается на монотонные части следует из предыдущей леммы. |
| − | ''' | + | Остаётся доказать, что диагонали, построенные в процессе выполнения алгоритма, попарно не пересекаются и не пересекают стороны <tex>P</tex>. |
| − | + | ||
| − | + | Рассмотрим случай выполнения функции ''HandleSplitVertex'', поскольку это наиболее общий случай: split вершина может быть соединена со всеми типами вершин, в отличие от остальных функций (в них рассматриваемая в данный момент вершина может быть соединена только с merge вершиной). | |
| − | + | ||
| − | + | Допустим, что диагональ <tex>v_{i}v_{m}</tex> была построена с помощью ''HandleSplitVertex'' по достижению split вершины <tex>v_i</tex>. Рассмотрим четырёхугольник <tex>H</tex>, заключённый между <tex>e_j</tex> и <tex>e_k</tex> - левым и правым ребром относительно <tex>v_i</tex> и горизонтальными прямыми, проведёнными через <tex>v_i</tex> и <tex>v_m</tex>. Внутри <tex>H</tex>, не может находиться ни одной из вершин <tex>P</tex>, в противном случае <tex>helper(e_j)</tex> не равнялся бы <tex>v_m</tex>. Предположим теперь, что <tex>v_{i}v_{m}</tex> пересекает <tex>e_s</tex> одну из сторон <tex>P</tex>. Учитывая, что никаких вершин <tex>P</tex> не лежит внутри <tex>H</tex> и стороны <tex>P</tex> не пересекаются, то <tex>e_s</tex> должна пересечь либо отрезок, соединяющий <tex>e_j</tex> и <tex>v_m</tex>, либо <tex>e_j</tex> и <tex>v_i</tex>.[[Файл:Pic_of_correctness.jpg|400px|thumb|right|1) Вершин внутри <tex>H</tex> находиться не может; 2) <tex>v_{i}v_m</tex> может пересекать только рёбра, помеченные зелёным]] Такое возможно только в случае, когда точками пересечения будут являться <tex>v_i</tex> или <tex>v_m</tex>, что не противоречит условию. Отсюда <tex>v_{i}v_{m}</tex> не пересекает ни одну из сторон <tex>P</tex> в посторонних точках. | |
| − | ''' | + | |
| − | }}</ | + | |
| + | Теперь рассмотрим случай с пересечением добавленной ранее диагональю. Поскольку внутри <tex>H</tex> никаких вершин вершин находиться не может, и оба конца любой добавленной ранее диагонали должны лежать выше <tex>v_i</tex>, диагональ <tex>v_{i}v_m</tex> не может пересекать никакую из ранее добавленных диагоналей. | ||
| + | }} | ||
| + | ===== Оценка работы ===== | ||
| + | Построение описанной выше приоритетной очереди <tex>Q</tex> происходит за линейное время. Когда заметающая прямая останавливается в вершине: операции с очередью занимают константу по времени, операции с деревом <tex>T</tex> на запросы и обновления требуют <tex>\mathcal{O}(\mathcal \log n)</tex>. Добавление диагонали в <tex>D</tex> требует <tex>\mathcal{O}(1)</tex>. В итоге обработка каждой вершины требует <tex>\mathcal{O}(\log n)</tex>, а весь алгоритм соответственно <tex>\mathcal{O}(n \log n)</tex>. Что касается памяти, она очевидно составляет <tex>\mathcal{O}(n) </tex>. Очередь <tex>Q</tex> и дерево <tex>T</tex> занимают линейную память. | ||
| + | |||
| + | [[Файл:Triangulationg intro.jpg|170px|thumb|right|Зелёным помечена так называемая воронка, которая образуется, когда мы достигнем красной вершины]] | ||
| + | |||
| + | == Триангуляция монотонного многоугольника == | ||
| + | Будем проходить сверху вниз по вершинам многоугольника проводя диагонали где это возможно. | ||
| + | |||
| + | Отсортируем все вершины многоугольника <tex>P</tex> в порядке убывания их <tex>y</tex>-координаты. Заведём стек вершин <tex>S</tex>. В стеке будем хранить вершины в отсортированном порядке, которые были обработаны, но не были отрезаны от многоугольника, то есть находятся в той части многоугольника, которая ещё не была триангулирована. В момент обработки некоторой вершины, будем пытаться провести из неё как можно больше диагоналей к вершинам, содержащимся в стеке. Эти диагонали отрезают треугольники от <tex>P</tex>. На вершине стека будет храниться вершина, которая будет обрабатываться последней. | ||
| + | |||
| + | Часть многоугольника <tex>P</tex>, лежащая выше последней обработанной вершины <tex>v_i</tex> и которая ещё не была триангулирована имеет форму перевёрнутой воронки (см. рисунки). Одна сторона воронки состоит из одной из сторон <tex>P</tex>, а другая состоит из цепи вершин, которые лежат выше <tex>v_i</tex> и внутренние углы которых не меньше <tex>\pi</tex>. Несложно догадаться, что самая нижняя вершина стека является единственной выпуклой. Несложно также заметить, что при обработке следующей вершины свойство перевёрнутой воронки сохранится, то есть оно является инвариантом алгоритма. | ||
| + | |||
| + | [[Файл:Triang_alg_case1.jpg|200px|thumb|left|Первый случай. Синим помечены стороны воронки, зелёным — диагонали, а жёлтым границы новой ещё не протриангулированной области]] | ||
| + | [[Файл:Triang alg case2.jpg|300px|thumb|right|Второй случай. Синим помечена цепь из вершин, которая содержится в стеке <tex>S</tex> на момент достижения вершины <tex>v_j</tex>, рыжей помечена первая вершина, до которой невозможно провести диагональ, жёлтой помечена новая нетриангулированная область <tex>P</tex> в форме воронки]] | ||
| + | === Алгоритм === | ||
| + | Рассмотрим процесс обработки вершины более подробно. Возможны два случая: | ||
| + | * Текущая вершина <tex>v_j</tex> является нижним концом стороны <tex>e</tex>, ограничивающего воронку. Вершины противоположной цепи уже были положены в стек. В этом случае можно просто построить диагонали, соединяющие <tex>v_j</tex> со всеми вершинами, находящимися в стеке, кроме последней. Последняя вершина в стеке уже соединена с <tex>v_j</tex> стороной <tex>e</tex>. Часть многоугольника <tex>P</tex>, лежащая выше <tex>v_j</tex>, которая не была триангулирована, ограничена диагональю, которая соединяет <tex>v_j</tex> с вершиной <tex>v_{s1}</tex>, которая была первой в стеке. Сторона многоугольника <tex>P</tex>, выходящая из <tex>v_{s1}</tex> направлена вниз. Снова образуется фигура c одним выпуклым углом, похожая на воронку — инвариант сохраняется. Вершины <tex>v_j</tex> и <tex>v_{s1}</tex> кладутся в стек, поскольку они были были обработаны, но по прежнему являются вершинами непротриангулированной части <tex>P</tex>. | ||
| + | |||
| + | * Вершина <tex>v_j</tex> принадлежит последовательной цепи вершин, добавленных в <tex>S</tex>. Вынем из стека верхнюю вершину <tex>v_{s1}</tex> — она уже соединена с <tex>v_{j}</tex> одной из сторон <tex>P</tex>. Затем будем пытаться выстраивать диагонали, соединяющие <tex>v_{j}</tex> c вынимаемыми из стека вершинами пока это возможно. Проверку на возможность построения диагонали <tex>v_{j}v_{k}</tex>, где <tex>v_{k}</tex> — текущая верхняя вершина стека, можно осуществлять посредством изучения взаимного расположения предыдущей вершины, вынутой из <tex>S</tex>, относительно <tex>v_{j}v_{k}</tex>. Когда мы достигнем вершины <tex>v_{k}</tex>, до которой невозможно провести диагональ, положим предыдущую вершину <tex>v_{k-1}</tex> обратно в стек. Вершина <tex>v_{k-1}</tex> является либо последней, до которой было возможно провести диагональ, либо, если ни одной диагонали из <tex>v_{j}</tex> провести не удалось, — соседом <tex>v_{j}</tex>. Далее положим <tex>v_{j}</tex> в стек. Опять же инвариант непротриангулированной части <tex>P</tex> сохраняется: одна сторона воронки ограничена частью стороны многоугольника, а другая цепью невыпуклых вершин. | ||
| + | |||
| + | === Псевдокод === | ||
| + | Как ранее уже было отмечено, задаём <tex>P</tex> в виде рёберного списка c двойными связями <tex>D</tex>. | ||
| + | TriangulateMonotonePolygon(P) | ||
| + | vertex [n] V = new vertex(P); // массив вершин <tex>P</tex>, отсортированный по y-координате в порядке убывания. | ||
| + | stack S = new stack(); | ||
| + | S.push(V[1]); | ||
| + | S.push(V[2]); | ||
| + | for j <tex>\leftarrow</tex> 3 to n - 1 | ||
| + | if (V[j] = S.peek()) | ||
| + | while (S <tex>\neq \varnothing </tex>) | ||
| + | if (S.size() <tex>\neq</tex> 1) | ||
| + | Insert edge(V[j], S.peek()) in D | ||
| + | S.pop() | ||
| + | S.push(V[j-1]) | ||
| + | S.push(V[j]); | ||
| + | else | ||
| + | vertex last <tex>\leftarrow</tex> S.peek(); | ||
| + | S.pop(); | ||
| + | while (IsValidDiagonal(edge(V[j], S.peek()), last)) //проверка возможности построения | ||
| + | //диагонали — предикат "левый поворот" | ||
| + | last <tex>\leftarrow</tex> S.peek(); | ||
| + | S.pop(); | ||
| + | Insert edge(V[j], last) in D | ||
| + | S.push(last); | ||
| + | S.push(V[j]); | ||
| + | S.pop() | ||
| + | while (S <tex>\neq \varnothing </tex>) | ||
| + | if (S.size() <tex>\neq</tex> 1) | ||
| + | Insert edge(V[j], S.peek()) in D | ||
| + | S.pop() | ||
| + | === Корректность === | ||
| + | * Все построенные диагонали попарно не пересекаются. Это гарантируется тем, что при каждом просмотре определённой вершины рассматривается только та часть <tex>P'</tex> многоугольника <tex>P</tex>, которая не была протриангулирована, следовательно внутри этой области по определению не может лежать ни одной из уже построенных диагоналей. Несложно заметить, что в стеке <tex>S</tex> на каждой итерации главного цикла хранятся вершины, которые принадлежат именно <tex>P'</tex> и лежат выше рассматриваемой вершины. | ||
| + | * Количество построенных диагоналей всегда будет <tex>n-3</tex>, поэтому непротриангулированных частей в многоугольнике не останется. | ||
| + | === Оценка работы === | ||
| + | Построение массива вершин требует линейное время и занимает линейную память. Главный цикл ''for'' выполняется <tex>n-3</tex> раза. Каждая его итерация может потребовать линейное время. Однако заметим, что на каждой итерации главного цикла в стек кладутся максимум две вершины, следовательно общее число выполнения операции ''push'', включая первые две вершины, положенные в начале алгоритма, ограничено <tex>2n-4</tex>. Количество операций ''pop'' за время работы алгоритма не превысит количества операций ''push''. Отсюда общее время работы цикла ''for'' <tex>\mathcal{O}(n)</tex>. В итоге общее время работы <tex>\mathcal{O}(n)</tex>. | ||
| + | === Общая оценка === | ||
| + | Разбиение многоугольника на монотонные части занимает <tex>\mathcal{O}(n \log n)</tex> времени и <tex>\mathcal{O}(n)</tex> памяти. Триангуляция каждой из частей занимает линейную память и время. Учитывая то, что суммарное количество вершин во всех частях <tex>\mathcal{O}(n)</tex>, триангуляция всех частей займёт <tex>\mathcal{O}(n)</tex> по времени и по памяти. | ||
| − | + | В итоге общая оценка составляет <tex>\mathcal{O}(n \log n)</tex> по времени и <tex>\mathcal{O}(n)</tex> по памяти. | |
| − | < | ||
| − | |||
| − | </ | ||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Версия 22:40, 20 января 2015
Содержание
Монотонный метод
| Определение: |
| Простой многоугольник называется монотонным относительно прямой , если любая , такая что , пересекает стороны не более двух раз (результатом пересечения и может быть только один отрезок или точка). |
| Определение: |
| Многоугольник, монотонный относительно -оси называется -монотонным. |
Суть данного метода заключается в том, чтобы разбить многоугольник на монотонные части, а затем триангулировать каждую из них.
Разбиение многоугольника на монотонные части =
Рассмотрим самую верхнюю — максимальную по координате вершину. Будем идти вниз по рёбрам до самой нижней — соотвественно минимальной по вершине, то есть таким образом, что для некоторой вершины : . Поворотной назовём вершину , на которой направление обхода будет меняется: и . Опишем более подробно этот тип вершин. Уточним понятния выше и ниже: точка лежит ниже точки , если или если и , соответственно точка лежит выше точки , если или если и . Это было сделано для того, чтобы избежать неопределённых ситуаций с вершинами, у которых -координаты равны.
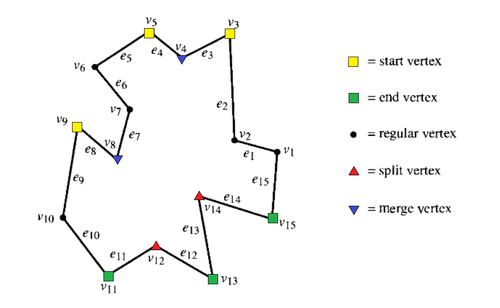
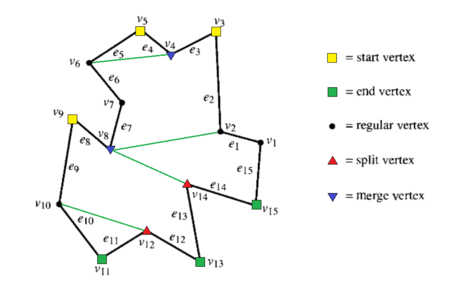
Обозначим за внутренний угол при некоторой вершине и определим далее пять типов вершин, четыре из которых являются поворотными:
- start вершина — два её соседа лежат ниже её самой и
- split вершина — два её соседа лежат ниже её самой и
- end вершина — два её соседа лежат выше её самой и
- merge вершина — два её соседа лежат выше её самой и
- regular вершина — не является поворотной, в отличие от остальных, другими словами один её сосед находится выше, а другой ниже её самой.
| Лемма: |
Многоугольник является -монотонным, если в нём отсутствуют split и merge вершины. |
| Доказательство: |
|
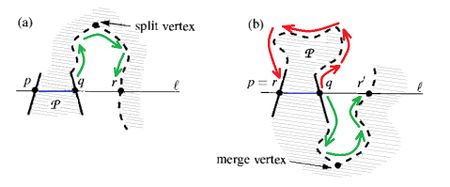
Предположим, что не -монотонный. Тогда докажем, что содержит split и merge вершины. Поскольку не -монотонный, существует горизонтальная прямая , которая пересекает его стороны более двух раз. Выберем таким образом, чтобы самой левой компонентой пересечения и был бы отрезок . Далее будем двигаться наверх по сторонам , начиная от точки . В результате в некоторой точке , где (случай (a) на рисунке), прямая снова пересечёт одну из сторон . Отсюда самая высокая точка, которую мы достигли во время движения по сторонам , будет split вершиной. Если же (случай (b) на рисунке), начём опять двигаться по сторонам теперь уже вниз. Как и в предыдущем случае найдётся некоторая точка , которая будет результатом пересечения и . При этом , в противном случае будет пересекать только два раза, что противоречит выбору . Аналогично предыдущему случаю, выберем теперь самую низкую точку, которую мы достигли во время движения по сторонам P. Она будет merge вершиной. |
Алгоритм
Чтобы сделать многоугольник монотонным, нужно избавиться от split и merge вершин путём проведения непересекающихся дигоналей из таких вершин.
Рассмотрим горизонтальную заметающую прямую , будем перемещать её сверху вниз вдоль плоскости на которой лежит исходный многоугольник . Будем останавливать её в каждой вершине многоугольника. В тот момент, когда на пути заметающей прямой встречается split или merge вершина её нужно соединить с вершиной, у которой расстояние до минимально, при этом она должна лежать соответственно выше или ниже .
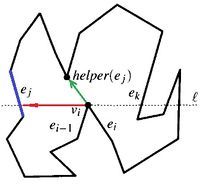
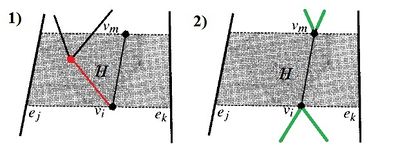
Рассмотрим каждый случай подробнее:- Split вершина. Пусть и — ближайшее левое и правое ребро относительно split вершины , которые пересекает в данный момент. Нам нужно найти вершину, лежащую между и , наиболее приближённую к , либо если такой точки не существет выбрать минимальную из верхних вершин и . Для этого будем хранить указатель на искомую вершину у левого ребра , который можно заранее вычислить. Тип вершины, хранящийся в не имеет значения. Таким образом, чтобы построить диагональ для split вершины нужно обратиться к указателю её левого ребра, которое пересекает в данный момент.
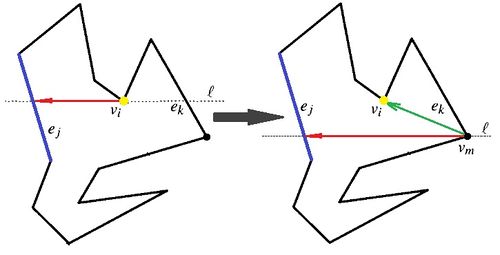
- Merge вершина. В отличие от случая со split вершиной заранее вычислить указатель нельзя, поскольку merge вершина должна быть соединена с вершиной, лежащей ниже заметающей прямой . Для этого в - левого относительно ребра запишем саму . Далее спускаем заметающую прямую вниз к следующей вершине , обращаемся к 'у её левого ребра. Проверяем, если там хранится merge вершина, строим диагональ . Последняя проверка осуществляется для любого типа вершины, кроме split, согласно п.1.
Структуры данных
В подходе, описанном выше, требуется находить пересечения заметающей прямой и левых ребёр многоугольника. Создадим двоичное дерево поиска , в листьях которого будем хранить рёбра, пересекающие , такие, что внутренняя область многоугольника будет лежать справа от них самих. С каждым таким ребром будем хранить его . Порядок следования листьев в дереве соответствует порядку следования рёбер в многоугольнике: слева направо. Дерево изменяется в зависимости от текущего состояния заметающей прямой. Создадим приоритетную очередь из вершин, в которой приоритетом будет -координата вершины. Если две вершины имеют одинаковые -координаты, больший приоритет у левой. Вершины будут добавляться на "остановках" заметающей прямой.
Многоугольник и добавленные в процессе диагонали удобно хранить в виде списка рёбер с двойными связями (DCEL — doubly-connected edge list), так как потом это обеспечит эффективный доступ к каждой из частей, которые нужно будет триангулировать.
Псевдокод
MakeMonotone(P) Construct(D); Construct(Q); // функция Construct создаёт объекты и , описанные выше. bst T = new bst(); while Q Remove from Q // удаление вершины с наивысшим приоритетом из switch (Type_of_vertex()): // определение типа вершины case 'start': HandleStartVertex(); case 'end': HandleEndVertex(); case 'split': HandleSplitVertex(); case 'merge': HandleMergeVertex(); case 'regular': HandleRegularVertex();
Опишем теперь каждый метод из последнего switch:
HandleStartVertex() Insert in T
HandleSplitVertex() edge = Search in T Insert edge(, ) in D Insert in T
В последующих трех функциях обработки вершины происходит обращение к смежному ребру . Это сделано для вершин, относительно которых внутренняя область лежит справа от них самих (вершина ), либо для двух подряд идущих merge вершин, таких как и .
HandleEndVertex() if (Type_of_vertex( = 'merge') Insert edge(, ) in D Delete from T
HandleMergeVertex() if (Type_of_vertex( = 'merge') Insert edge(, ) in D Delete from T edge = Search in T if (Type_of_vertex( = 'merge') Insert edge(, ) in D
HandleRegularVertex() if (interior of lies to the right of ) then if (Type_of_vertex( = 'merge') Insert edge(, ) in D Delete from T Insert in T else edge = Search in T if (Type_of_vertex( = 'merge') Insert edge(, ) in D
Корректность
| Лемма: |
Функция MakeMonotone(P) корректно выполняет разбиение многоугольника . Другими словами эта функция добавляет в множество непересекающихся диагоналей, которые разбивают на монотонные части. |
| Доказательство: |
|
Тот факт, что разбивается на монотонные части следует из предыдущей леммы. Остаётся доказать, что диагонали, построенные в процессе выполнения алгоритма, попарно не пересекаются и не пересекают стороны . Рассмотрим случай выполнения функции HandleSplitVertex, поскольку это наиболее общий случай: split вершина может быть соединена со всеми типами вершин, в отличие от остальных функций (в них рассматриваемая в данный момент вершина может быть соединена только с merge вершиной). Допустим, что диагональ была построена с помощью HandleSplitVertex по достижению split вершины . Рассмотрим четырёхугольник , заключённый между и - левым и правым ребром относительно и горизонтальными прямыми, проведёнными через и . Внутри , не может находиться ни одной из вершин , в противном случае не равнялся бы . Предположим теперь, что пересекает одну из сторон . Учитывая, что никаких вершин не лежит внутри и стороны не пересекаются, то должна пересечь либо отрезок, соединяющий и , либо и . Такое возможно только в случае, когда точками пересечения будут являться или , что не противоречит условию. Отсюда не пересекает ни одну из сторон в посторонних точках.
|
Оценка работы
Построение описанной выше приоритетной очереди происходит за линейное время. Когда заметающая прямая останавливается в вершине: операции с очередью занимают константу по времени, операции с деревом на запросы и обновления требуют . Добавление диагонали в требует . В итоге обработка каждой вершины требует , а весь алгоритм соответственно . Что касается памяти, она очевидно составляет . Очередь и дерево занимают линейную память.
Триангуляция монотонного многоугольника
Будем проходить сверху вниз по вершинам многоугольника проводя диагонали где это возможно.
Отсортируем все вершины многоугольника в порядке убывания их -координаты. Заведём стек вершин . В стеке будем хранить вершины в отсортированном порядке, которые были обработаны, но не были отрезаны от многоугольника, то есть находятся в той части многоугольника, которая ещё не была триангулирована. В момент обработки некоторой вершины, будем пытаться провести из неё как можно больше диагоналей к вершинам, содержащимся в стеке. Эти диагонали отрезают треугольники от . На вершине стека будет храниться вершина, которая будет обрабатываться последней.
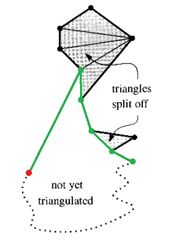
Часть многоугольника , лежащая выше последней обработанной вершины и которая ещё не была триангулирована имеет форму перевёрнутой воронки (см. рисунки). Одна сторона воронки состоит из одной из сторон , а другая состоит из цепи вершин, которые лежат выше и внутренние углы которых не меньше . Несложно догадаться, что самая нижняя вершина стека является единственной выпуклой. Несложно также заметить, что при обработке следующей вершины свойство перевёрнутой воронки сохранится, то есть оно является инвариантом алгоритма.
Алгоритм
Рассмотрим процесс обработки вершины более подробно. Возможны два случая:
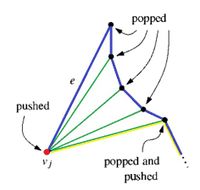
- Текущая вершина является нижним концом стороны , ограничивающего воронку. Вершины противоположной цепи уже были положены в стек. В этом случае можно просто построить диагонали, соединяющие со всеми вершинами, находящимися в стеке, кроме последней. Последняя вершина в стеке уже соединена с стороной . Часть многоугольника , лежащая выше , которая не была триангулирована, ограничена диагональю, которая соединяет с вершиной , которая была первой в стеке. Сторона многоугольника , выходящая из направлена вниз. Снова образуется фигура c одним выпуклым углом, похожая на воронку — инвариант сохраняется. Вершины и кладутся в стек, поскольку они были были обработаны, но по прежнему являются вершинами непротриангулированной части .
- Вершина принадлежит последовательной цепи вершин, добавленных в . Вынем из стека верхнюю вершину — она уже соединена с одной из сторон . Затем будем пытаться выстраивать диагонали, соединяющие c вынимаемыми из стека вершинами пока это возможно. Проверку на возможность построения диагонали , где — текущая верхняя вершина стека, можно осуществлять посредством изучения взаимного расположения предыдущей вершины, вынутой из , относительно . Когда мы достигнем вершины , до которой невозможно провести диагональ, положим предыдущую вершину обратно в стек. Вершина является либо последней, до которой было возможно провести диагональ, либо, если ни одной диагонали из провести не удалось, — соседом . Далее положим в стек. Опять же инвариант непротриангулированной части сохраняется: одна сторона воронки ограничена частью стороны многоугольника, а другая цепью невыпуклых вершин.
Псевдокод
Как ранее уже было отмечено, задаём в виде рёберного списка c двойными связями .
TriangulateMonotonePolygon(P) vertex [n] V = new vertex(P); // массив вершин , отсортированный по y-координате в порядке убывания. stack S = new stack(); S.push(V[1]); S.push(V[2]); for j 3 to n - 1 if (V[j] = S.peek()) while (S ) if (S.size() 1) Insert edge(V[j], S.peek()) in D S.pop() S.push(V[j-1]) S.push(V[j]); else vertex last S.peek(); S.pop(); while (IsValidDiagonal(edge(V[j], S.peek()), last)) //проверка возможности построения //диагонали — предикат "левый поворот" last S.peek(); S.pop(); Insert edge(V[j], last) in D S.push(last); S.push(V[j]); S.pop() while (S ) if (S.size() 1) Insert edge(V[j], S.peek()) in D S.pop()
Корректность
- Все построенные диагонали попарно не пересекаются. Это гарантируется тем, что при каждом просмотре определённой вершины рассматривается только та часть многоугольника , которая не была протриангулирована, следовательно внутри этой области по определению не может лежать ни одной из уже построенных диагоналей. Несложно заметить, что в стеке на каждой итерации главного цикла хранятся вершины, которые принадлежат именно и лежат выше рассматриваемой вершины.
- Количество построенных диагоналей всегда будет , поэтому непротриангулированных частей в многоугольнике не останется.
Оценка работы
Построение массива вершин требует линейное время и занимает линейную память. Главный цикл for выполняется раза. Каждая его итерация может потребовать линейное время. Однако заметим, что на каждой итерации главного цикла в стек кладутся максимум две вершины, следовательно общее число выполнения операции push, включая первые две вершины, положенные в начале алгоритма, ограничено . Количество операций pop за время работы алгоритма не превысит количества операций push. Отсюда общее время работы цикла for . В итоге общее время работы .
Общая оценка
Разбиение многоугольника на монотонные части занимает времени и памяти. Триангуляция каждой из частей занимает линейную память и время. Учитывая то, что суммарное количество вершин во всех частях , триангуляция всех частей займёт по времени и по памяти.
В итоге общая оценка составляет по времени и по памяти.