Участник:Warmte
HyperLogLog — это вероятностный алгоритм, оценивающий количество различных элементов в больших потоках данных. Является стриминговым алгоритмом (англ. streaming algorithm), то есть обрабатывает последовательно поступающие данные в один проход.
Подобные алгоритмы используются в тех случаях, когда объемы обрабатываемых данных настолько велики, что получение точного ответа затребует пропорционально слишком большого объёма памяти, в то время как вероятностный алгоритм может дать близкий к точному ответ, будучи с точки зрения памяти намного более оптимальным.
Точность
При использовании единиц дополнительной памяти алгоритм HyperLogLog оценивает количество различных элементов со стандартной ошибкой около , то есть при оценке данных > 109 этому алгоритму потребуется всего 1.5 kB памяти для получения ответа с точностью 2%.
Предыдущий алгоритм LogLog, использовавшийся для решения этой задачи, достигал сравнимой точности ответа при использовании 64% от оригинальных объемов памяти.
Идея алгоритма
В основе алгоритма HyperLogLog лежит наблюдение, что мощность набора равномерно распределенных случайных чисел можно оценить, вычислив максимальное количество ведущих нулей в двоичном представлении каждого числа в наборе. Таким образом, если максимальное наблюдаемое количество начальных нулей равно , то оценка количества различных элементов в наборе будет .
Суть алгоритма заключается в следующем: к каждому элемента исходного набора применяется хеш-функция для получения набора равномерно распределенных случайных чисел с той же мощностью, что и исходный набор. Затем мощность этого случайно распределенного набора оценивается с помощью описанного выше алгоритма.
Но при таком подходе могут возникать различные проблемы за счёт большой дисперсии получаемой величины, а также некоторых крайних случаев: к примеру, если хэш некоторого элемента будет равен , то максимальное количество ведущих нулей сразу станет равным , где — максимальное значение выбранной хэш-функции. Чтобы избежать подобных проблем и минимизировать дисперсию, модифицируем алгоритм следующим образом: разделим исходный поток элементов на корзин, для каждой из них вычислим максимальное наблюдаемое количество начальных нулей среди элементов в этой корзине, а затем на основе полученных для всех корзин значений вычислим итоговый ответ на задачу.
Описание алгоритма
- — исходный набор элементов .
- — выбранная хэш-функция с возможными значениями от до , .
- — количество бит исходного хэша, характеризующих номер корзины, в которую будет отправлен соответствующий элемент.
- — максимальное наблюдаемое количество начальных нулей в корзине под номером .
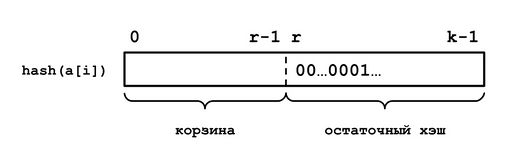
Разобьём исходный набор на наборы следующим образом: для каждого поступающего элемента вычислим его хэш и представим его в двоичном виде. Тогда первые бит этого двоичного представления будут характеризовать номер корзины , а оставшиеся биты сформируют остаточный хэш , который и будет использоваться для поиска максимального количества начальных нулей в корзине .
Для каждой корзины вычислим соответствующее , равное максимальному количеству ведущих нулей среди элементов этой корзины. Тогда оценкой для числа различных элементов в корзине будет .
Логично было бы предположить, что в таком случае итоговым ответом на задачу будет , но такой подход приводит не к самому выгодному результату. Выгоднее всего будет пересчитывать результат при помощи среднего гармонического всех полученных оценок:
- — это индикатор, вычисляемый по формуле
- — корректирующий множитель, вычисляемый по формуле .
Поскольку множитель может быть достаточно сложным для вычисления, можно подобрать его примерное значение в зависимости от :
Асимптотика
Оценка времени работы: , где — количество элементов в исходном наборе.
Оценка дополнительной памяти: , где — количество возможных значений хэш-функции.