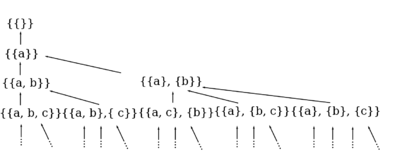Числа Белла — различия между версиями
(→References) |
м (rollbackEdits.php mass rollback) |
||
| (не показаны 222 промежуточные версии 13 участников) | |||
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
| − | |definition = В комбинаторной математике числа Белла | + | |definition = В комбинаторной математике '''числа Белла''' (''англ. Bell's numbers'') определяют количество возможных способов [[Комбинаторные объекты#Разбиение на подмножества|разбиения множества]] из <tex>n</tex> элементов на подмножества. |
}} | }} | ||
| − | Числа Белла начинаются с | + | Числа Белла начинаются с <tex dpi="130">B_0=B_1=1</tex> и образуют последовательность: |
| − | :1, 1,2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, 27644437, 190899322, 1382958545, 10480142147, 82864869804, 682076806159, 5832742205057 | + | :<tex dpi="130">1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, 27644437, |
| − | + | 190899322, 1382958545, 10480142147, 82864869804, 682076806159, 5832742205057\dots | |
| − | + | </tex> | |
| + | <tex dpi="130">n</tex>-й элемент множества чисел Белла, <tex dpi="130">B_n</tex>, определяет количество различных способов разбиения множества, то есть количество [[Отношение эквивалентности|отношений эквивалентности]] в нем. | ||
==Подсчет== | ==Подсчет== | ||
| − | + | [[File:XxxCircles.png|400px|thumb|upright|52 разбиения множества из 5 элементов]] | |
| − | [[File: | + | [[File:Order.png|400px|border]] |
| − | [[File: | ||
| − | |||
| − | + | Разбиение множества <tex dpi="130">S</tex> определяется как совокупность '''попарно непересекающихся подмножеств множества''' <tex dpi="130">S</tex>. Например, <tex>B_3 = 5</tex>, потому что множество, состоящее их <tex>3</tex> элементов <tex> \{ a, b , c \} </tex> может быть разделено <tex>5</tex> различными способами: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | :<tex> \{ a \} , \{ b \} , \{ c \} </tex> | |
| − | + | : <tex> \{ a \} , \{b, c \} </tex> | |
| − | + | : <tex> \{ b \} , \{a, c \} </tex> | |
| − | :{ | + | : <tex> \{ c \} , \{ a, b \} </tex> |
| − | :{ | + | : <tex> \{ a, b , c \} </tex> |
| − | :{ | ||
| − | |||
| − | == | + | <tex dpi="130">B_0 = 1</tex>, т.к. существует только одно возможное разбиение пустого множества. Пустое множество может разбиваться только на само себя. |
| − | + | Как было обозначено выше, мы '''не рассматриваем ни порядок подмножеств, ни порядок элементов в каждом их них'''. Это означает, что данные разбиения являются идентичными: | |
| − | + | : <tex> \{ b \} , \{ a , c \} </tex> | |
| − | :<tex> | + | : <tex>\{ a, c\}, \{ b \} </tex> |
| − | + | : <tex>\{ b \}, \{ c, a \} </tex> | |
| − | + | : <tex>\{ c, a \}, \{ b \} </tex> | |
| − | |||
| − | + | В противном случае, если различные упорядочивания множеств считаются различными разбиениями, тогда количество таких упорядоченных разбиений называются '''упорядоченными числами Белла'''. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Факторизации== | |
| + | Если число <tex dpi="130">N</tex>является свободным от квадратов <ref>[[wikipedia:Square-free element|Wikipedia {{---}} Cвободные от квадратов числа]]</ref>, то <tex dpi="130">B_n</tex> показывает количество различных мультипликативных разбиений <tex dpi="130">N</tex>. | ||
| + | Если <tex dpi="130">N</tex> является квадратичным положительным целым числом (является произведением некоторого числа <tex dpi="130">n</tex> различных простых чисел), то <tex dpi="130">B_n</tex> дает '''число различных мультипликативных разбиений''' <tex dpi="130">N</tex>. Это является факторизацией <tex dpi="130">N</tex> в числа большие, чем <tex>1</tex> (рассматривая две факторизации как идентичные, если они имеют одинаковые факторы в другом порядке.) подтверждает это наблюдение Сильвио Минетоле<ref> Williams 1945 credits this observation to Silvio Minetola's Principii di Analisi Combinatoria (1909).</ref>. | ||
| + | Например, <tex>30</tex> является произведением <tex>3</tex> простых чисел <tex>2</tex>, <tex>3</tex> и <tex>5</tex> и имеет <tex dpi="130">N=5 </tex> факторизаций: | ||
| + | :<tex>30 = 2\times 15=3\times 10=5\times 6=2\times 3\times 5</tex> | ||
| − | + | ==Схемы рифмовки== | |
| − | + | Числа Белла показывают ''количество схем рифмовки на <tex dpi="130">n</tex> строках''. Схема рифмы описывает, какие строки рифмуются друг с другом, и поэтому может быть истолковано как отношение экивалентности на множестве строк. Таким образом, <tex>15</tex> возможных четверостиший схемами рифмовки являются: | |
| − | + | <tex dpi="130"> AAAA, AAAB, AABA, AABB, AABC, ABAA, ABAB, ABAC, | |
| − | + | ABBA, ABBB, ABBC, ABCA, ABCB, ABCC, ABCD</tex>. | |
| − | |||
==Свойства== | ==Свойства== | ||
===Формулы суммирования=== | ===Формулы суммирования=== | ||
| − | Числа Белла удовлетворяют рекуррентному соотношению c участием биномиальных коэффициентов | + | ====Биномиальные коэффициенты==== |
| − | :<tex>B_{n+1}=\sum_{k=0}^{n} \binom{n}{k} B_k.</tex> | + | Числа Белла удовлетворяют рекуррентному соотношению c участием биномиальных коэффициентов: |
| − | + | :<tex dpi = "150">B_{n+1}=\sum_{k=0}^{n} \binom{n}{k} B_k.</tex> | |
| − | + | ==== Доказательство ==== | |
| − | + | Докажем, что <tex dpi = "150">B_{n+1}=\sum_{k=0}^{n} \binom{n}{k} B_{n-k}.</tex> По определению <tex dpi = "150">B_{n}\ { — }\ </tex>число всех неупорядоченных подмножеств <tex>n</tex>-элементного множества. Посчитаем количество неупорядоченных подмножеств для <tex dpi= "150">(n+1)</tex>-элементного множества множества: Пусть <tex dpi= "150">x_1 \cup... \cup x_k\ { — }\ </tex>подмножества множества <tex dpi= "150">[1...n+1]</tex>. Пусть <tex dpi= "150">n+1\in x_k</tex>, тогда <tex dpi= "150">x_1 \cup... \cup x_{k-1}\ { — }\ </tex>подмножество множества <tex dpi="150">[1...n+1]</tex> \ <tex dpi= "150">x_k</tex>. Пусть <tex dpi= "150">|x_k|=i+1</tex>, где <tex dpi= "150">i\in [0;n]</tex>, тогда <tex dpi= "150">x_k</tex> можно выбрать <tex dpi= "150">\binom{n}{i}</tex> способами, а оставшиеся элементы разбить <tex dpi = "150">B_{n-i}</tex> способами. <tex dpi = "150">B_{n+1}=\sum_{k=0}^{n} \binom{n}{k} B_{n-k}=</tex> <tex dpi = "150">\sum_{k=0}^{n} \binom{n}{n-k} B_{k}=</tex> <tex dpi= "150">\sum_{k=0}^{n} \binom{n}{k} B_k</tex>. | |
| − | |||
| − | |||
| − | === | + | ====Связь с числами Стирлинга второго рода==== |
| − | Экспоненциальной производящей функцией | + | Другая формула суммирования представляет каждое число Белла как сумму [[Числа Стирлинга второго рода|'''чисел Стирлинга второго рода''']]: |
| − | :<tex>B(x) = \sum_{n=0}^\infty \frac{B_n}{n!} x^n = e^{e^x-1}.</tex> | + | :<tex dpi = "150">B_n=\sum_{k=0}^n \left\{{n\atop k}\right\}</tex>, |
| + | где число Стирлинга <tex dpi = "150">\left\{{n\atop k}\right\}</tex> является количеством способов разбиения набора элементов <tex dpi = "150">n</tex> в ровно <tex dpi="150">k</tex> непустых подмножеств. | ||
| + | ==== Доказательство ==== | ||
| + | Посчитаем количество подмножеств <tex dpi= "150">n</tex>-элементного множества. Нам нужно разбить <tex dpi= "150">n</tex>-элементное множество на <tex dpi= "150">k</tex> непустых подмножеств, где <tex dpi= "150">k</tex> от <tex dpi= "150">1</tex> до <tex dpi= "150">n</tex>. Пусть | ||
| + | <tex dpi= "150">C\ { — }\ </tex>все подмножества <tex dpi= "150">n</tex>-элементного множества. Пусть <tex dpi= "150">A_k\ { — }\ </tex>разбиение <tex dpi= "150">n</tex>-элементного множества на <tex dpi= "150">k</tex> непустых подмножеств, тогда <tex dpi = "150"> C = \bigcup \limits_{k=1}^{n}A_k</tex>. <tex dpi = "150">|A_k|=\left\{{n\atop k}\right\}\ { — }\ </tex>по определению, тогда <tex dpi = "150">B_n=|C|=\sum_{k=1}^{n} \ |A_k|=\sum_{k=1}^n \left\{{n\atop k}\right\}=\sum_{k=0}^n \left\{{n\atop k}\right\}</tex>, т.к. <tex dpi = "150">\left\{{n\atop 0}\right\}=0</tex>. | ||
| + | |||
| + | ====Объединяющая формула==== | ||
| + | Майкл Спайви<ref>Spivey, Michael Z. (2008). "A generalized recurrence for Bell numbers" . Journal of Integer Sequences. 11 (2): Article 08.2.5, 3. MR 2420912.</ref> получил формулу, которая объединяет оба эти суммирования: | ||
| + | :<tex dpi = "150">B_{n+m} = \sum_{k=0}^n \sum_{j=0}^m \left\{{m\atop j}\right\} {n \choose k} j^{n-k} B_k.</tex> | ||
| + | ==== Лемма ==== | ||
| + | <tex dpi = "150">B_{n+m}\ { — }\ </tex>количество способов разбить <tex dpi = "150">(n+m)</tex>-элементное множество на подмножества. Количество способов разбить <tex dpi = "150">m</tex>-элементное множество на <tex dpi = "150">j</tex> непустых подмножеств это <tex dpi = "150">\left\{{m\atop j}\right\}</tex>, где <tex dpi = "150">j</tex> меняется от <tex dpi = "150">1</tex> до <tex dpi = "150">m</tex>. Из оставшихся <tex dpi = "150">n</tex> объектов выберем <tex dpi = "150">k</tex>, для разделения их на новые подмножества, а оставшиеся <tex dpi = "150">n-k</tex> объектов распределим между <tex dpi = "150">j</tex> подмножествами, сформированных из <tex dpi = "150">m</tex>-элементного множества. <tex dpi = "150">B_{k}\ { — }\ </tex>количество разбиений <tex dpi = "150">k</tex>-элементного множества на подмножества и <tex dpi = "150">j^{n-k}</tex> способов разбить <tex dpi = "150">n-k</tex> элементов между <tex dpi = "150">j</tex> подмножествами. Значит <tex dpi = "150">j^{n-k} \left\{{n\atop k}\right\}\binom{n}{k} B_{k}</tex> способов разбить <tex dpi = "150">m</tex> элементов на <tex dpi = "150">j</tex> подмножеств и выбрать <tex dpi = "150">k</tex> элементов из <tex dpi = "150">n</tex>-элементного множества и выбрать <tex dpi = "150">k</tex> элементов из <tex dpi = "150">n </tex>-элементного множества и сформировать из них новые подмножества, а из оставшихся <tex dpi = "150">n-k</tex> объектов разделить между <tex dpi = "150">j</tex> множествами, сформированных из <tex dpi = "150">m</tex>-элементного множества. | ||
| + | |||
| + | ==== Доказательство ==== | ||
| + | Суммируя подмножества, рассмотренные в лемме, меняя <tex dpi = "150">m</tex> и <tex dpi = "150">k</tex>, получаем: | ||
| + | <tex dpi = "150">B_{n+m}=\sum_{k=0}^n \sum_{j=1}^m </tex><tex dpi = "150">\left\{{m\atop j}\right\}j^{n-k} \binom{n}{k} B_{k}=</tex><tex dpi = "150">B_{n+m}=\sum_{k=0}^n \sum_{j=0}^m </tex><tex dpi = "150">\left\{{m\atop j}\right\}j^{n-k} \binom{n}{k} B_{k}</tex> т.к. <tex dpi = "150">\left\{{m\atop 0}\right\}=0</tex>. | ||
| + | |||
| + | ===Производящая функция=== | ||
| + | Экспоненциальной [[производящая функция|производящей функцией]] чисел Белла является: | ||
| + | :<tex dpi = "150">B(x) = \sum_{n=0}^\infty \frac{B_n}{n!} x^n = e^{e^x-1}.</tex> | ||
Суммирование используется для определения экспоненциальной производящей функции для любой последовательности чисел. Правая часть является результатом выполнения суммирования в конкретном случае. | Суммирование используется для определения экспоненциальной производящей функции для любой последовательности чисел. Правая часть является результатом выполнения суммирования в конкретном случае. | ||
| + | |||
===Моменты распределения вероятностей=== | ===Моменты распределения вероятностей=== | ||
| − | Числа Белла удовлетворяют ''формуле Добинского'' | + | Числа Белла удовлетворяют '''формуле Добинского''': |
| − | :<tex>B_n=\frac{1}{e}\sum_{k=0}^\infty \frac{k^n}{k!}.</tex> | + | :<tex dpi = "150">B_n=\frac{1}{e}\sum_{k=0}^\infty \frac{k^n}{k!}.</tex> |
| − | Эта формула может быть получена за счет расширения экспоненциальной производящей функции, используя ряд Тейлора для экспоненциальной функции, а затем собирая условия с аналогичным показателем экспоненты. | + | Эта формула может быть получена за счет расширения экспоненциальной производящей функции, используя ряд Тейлора<ref>[[wikipedia:Taylor series|Ряд Тейлора]]</ref> для экспоненциальной функции, а затем собирая условия с аналогичным показателем экспоненты.<ref>Flajolet & Sedgewick (2009)</ref>. |
| − | Это позволяет интерпретировать ''B<sub>n</sub>'' как | + | Это позволяет интерпретировать ''B<sub>n</sub>'' как <tex dpi="130">n</tex>-й момент Пуассоновского распределения с ожидаемым значением <tex>1</tex>. |
===Интегральное представление=== | ===Интегральное представление=== | ||
| − | Применение интегральной формулы Коши для экспоненциальной производящей функции дает комплексное интегральное представление: | + | Применение интегральной формулы Коши <ref>[[wikipedia:Cauchy's integral formula|Формула Коши]]</ref> для экспоненциальной производящей функции дает комплексное интегральное представление: |
| − | : <tex> B_n = \frac{n!}{2 \pi i e} \int_{\gamma} \frac{e^{e^z}}{z^{n+1}} \, dz. </tex> | + | : <tex dpi = "150"> B_n = \frac{n!}{2 \pi i e} \int_{\gamma} \frac{e^{e^z}}{z^{n+1}} \, dz. </tex> |
| − | === | + | |
| − | Числа Белла формируют логарифмически выпуклую последовательность. Деление их на факториал, | + | ===Логарифмическая вогнутость=== |
| + | Числа Белла формируют логарифмически выпуклую последовательность. Деление их на факториал, <tex dpi = "170">\frac{B_n}{n!}</tex>, дает логарифмически выпуклую последовательность. | ||
| + | |||
===Темпы роста=== | ===Темпы роста=== | ||
| − | Известно несколько асимптотических формул для чисел Белла. | + | Известно несколько асимптотических формул для чисел Белла. |
| − | :<tex> B_n < \left( \frac{0.792 n}{\ln( n+1)} \right)^n </tex> для всех положительных чисел <tex>n</tex>; | + | '''Беренд Тасса''' в <tex>2010</tex>-м<ref>Berend, D.; Tassa, T. (2010). "Improved bounds on Bell numbers and on moments of sums of random variables". Probability and Mathematical Statistics. 30 (2): 185–205.</ref> установлил следующие границы: |
| + | :<tex dpi = "150"> B_n < \left( \frac{0.792 n}{\ln( n+1)} \right)^n </tex> для всех положительных чисел <tex>n</tex>; | ||
кроме того, если <tex> \varepsilon>0 </tex> затем для всех <tex> n > n_0(\varepsilon) </tex>, | кроме того, если <tex> \varepsilon>0 </tex> затем для всех <tex> n > n_0(\varepsilon) </tex>, | ||
| − | :<tex> B_n < \left( \frac{e^{-0.6 + \varepsilon} n}{\ln(n+1)}\right)^n </tex> | + | :<tex dpi = "150"> B_n < \left( \frac{e^{-0.6 + \varepsilon} n}{\ln(n+1)}\right)^n </tex> |
где <tex> ~n_0(\varepsilon) = \max\left\{e^4,d^{-1}(\varepsilon) \right\}~ </tex> и | где <tex> ~n_0(\varepsilon) = \max\left\{e^4,d^{-1}(\varepsilon) \right\}~ </tex> и | ||
| − | <tex> ~d(x) | + | <tex dpi = "150"> ~d(x)= \ln \ln (x+1) - \ln \ln x + \frac{1+e^{-1}}{\ln x}\,. |
</tex> | </tex> | ||
| − | Числа Белла могут быть аппроксимированы с помощью | + | Числа Белла могут быть аппроксимированы с помощью функции Ламберта <tex>W</tex> <ref> [[wikipedia:Lambert W function|Функция Ламберта W]]</ref>, данная функция имеет такой же темп роста, как логарифм, как |
| − | :<tex>B_n \sim \frac{1}{\sqrt{n}} \left( \frac{n}{W(n)} \right)^{n + \frac{1}{2}} \exp\left(\frac{n}{W(n)} - n - 1\right). </tex> | + | :<tex dpi = "150">B_n \sim \frac{1}{\sqrt{n}} \left( \frac{n}{W(n)} \right)^{n + \frac{1}{2}} \exp\left(\frac{n}{W(n)} - n - 1\right). </tex> |
| − | Moser Wyman | + | '''Мозер Л. и Вайман М.'''<ref>Moser, Leo; Wyman, Max (1955). "An asymptotic formula for the Bell numbers". Transactions of the Royal Society of Canada, Section III. </ref> установили расширение: |
| − | :<tex>B_{n+h} = \frac{(n+h)!}{W(n)^{n+h}} \times \frac{\exp(e^{W(n)} - 1)}{(2\pi B)^{1/2}} \times \left( 1 + \frac{P_0 + hP_1 + h^2P_2}{e^{W(n)}} + \frac{Q_0 + hQ_1 + h^2Q_2 + h^3Q_3 + h^4Q_4}{e^{2W(n)}} + O(e^{-3W(n)}) \right)</tex> | + | :<tex dpi = "150">B_{n+h} = \frac{(n+h)!}{W(n)^{n+h}} \times \frac{\exp(e^{W(n)} - 1)}{(2\pi B)^{1/2}} \times \left( 1 + \frac{P_0 + hP_1 + h^2P_2}{e^{W(n)}} + \frac{Q_0 + hQ_1 + h^2Q_2 + h^3Q_3 + h^4Q_4}{e^{2W(n)}} + O(e^{-3W(n)}) \right)</tex> |
Асимптотическое выражение | Асимптотическое выражение | ||
| − | :<tex> | + | :<tex dpi = "150"> |
| − | + | \frac{\ln B_n}{n} = \ln n - \ln \ln n - 1 + \frac{\ln \ln n}{\ln n} + \frac{1}{\ln n} + \frac{1}{2}\left(\frac{\ln \ln n}{\ln n}\right)^2 + O\left(\frac{\ln \ln n}{(\ln n)^2} \right) | |
| − | \frac{\ln B_n}{n} | + | \qquad \text{as }n\to\infty |
| − | |||
| − | |||
</tex> | </tex> | ||
| + | Было установлено '''де Брайном'''<ref>de Bruijn, N.G. (1981). Asymptotic methods in analysis (3rd ed.). Dover. p. 108.</ref> в <tex>1981</tex> году. | ||
| − | + | ==Получение== | |
| − | + | ===Вычисление с помощью треугольника Пирса=== | |
| − | + | [[Image:BellNumberAnimated.gif|right|thumb| Треугольное множество, правая диагональная последовательность которого состоит из чисел Белла]] | |
| − | + | Числа Белла могут быть с легкостью '''вычислены''' с помощью '''треугольника Белла''', который также называют '''массивом Айткена''' или '''треугольником Пирса'''. | |
| − | + | # Начнем с единицы. Помещаем ее в верхнюю строку. (<tex> x_{0,1} = 1 </tex>) | |
| − | + | # Каждая новая строка должна начинаться с крайнего правого элемента прошлой строки. (<tex>x_{i,1} \leftarrow x_{i-1, i}</tex>) | |
| − | + | # Заполняем строчку <tex>i</tex> по формуле <tex> ( x_{i,j} \leftarrow x_{i,j-1} + x_{i-1,j-1}) </tex> , начиная с <tex> j = 2 </tex>, пока <tex>j \leqslant i + 1 </tex>. | |
| − | + | # Крайнее левое число данной строки является числом Белла для этой строки. (<tex>B_i \leftarrow x_{i,1}</tex>) | |
| − | + | Первые пять строк треугольника, построенного по этим правилам: | |
| − | + | {| border="1" | |
| + | |- | ||
| + | |<tex>1</tex>|| || || || | ||
| + | |- | ||
| + | |<tex>1</tex>|| <tex>2</tex>|| || || | ||
| + | |- | ||
| + | | <tex>2</tex>||<tex>3</tex> ||<tex>5</tex> || || | ||
| + | |- | ||
| + | |<tex>5</tex>|| <tex>7</tex>|| <tex> 10</tex>|| <tex> 15</tex>|| | ||
| + | |- | ||
| + | |<tex>15</tex>|| <tex> 20</tex> || <tex>27</tex> || <tex>37</tex> || <tex>52</tex> | ||
| + | |} | ||
| + | ===Получение с помощью чисел Стирлинга второго рода=== | ||
| + | [[Числа Стирлинга второго рода|'''Числа Стирлинга второго рода''']] связаны друг с другом по следующей формуле: | ||
| + | <tex dpi="150">\left\{{n+1\atop k}\right\} = k \left\{{ n \atop k }\right\} + \left\{{n\atop k-1}\right\} | ||
| + | </tex> | ||
| + | Число Стирлинга второго рода показывает количество способов разбиения множества из <tex>n</tex> элементов на <tex>k</tex> непустых подмножеств. Если сложить все числа Стирлинга второго рода, имеющих одинаковую <tex>n</tex>, то получим количество способов разбиения множества из <tex>n</tex> элементов на непустых подмножеств, то есть <tex>n</tex>-ое число Белла. | ||
| + | |||
| + | Заполним таблицу чисел Стирлинга, используя формулу выше. | ||
| + | Cумма чисел <tex>n</tex>-ой строки будет являться <tex>n</tex>-ым числом Белла. | ||
| + | {| border="1" | ||
| + | |- | ||
| + | | n \ k ||<tex>0</tex>||<tex>1</tex>||<tex>2</tex>||<tex>3</tex>||<tex>4</tex>||Число Белла | ||
| + | |- | ||
| + | |<tex>0</tex>||<tex>1</tex>|| || || |||| |<tex>1</tex> | ||
| + | |- | ||
| + | |<tex>1</tex>||<tex>0</tex>|| <tex>1</tex>|| || |||| |<tex>1</tex> | ||
| + | |- | ||
| + | |<tex>2</tex>||<tex> 0</tex>||<tex>1</tex> ||<tex>1</tex> || || |||<tex>2</tex> | ||
| + | |- | ||
| + | |<tex>3</tex>||<tex>0</tex>|| <tex>1</tex>|| <tex>3</tex>|| <tex>1</tex>|||| |<tex>5</tex> | ||
| + | |- | ||
| + | |<tex>4</tex>||<tex>0</tex>|| <tex>1</tex> || <tex>7</tex> || <tex>6</tex> || <tex>1</tex> ||<tex>15</tex> | ||
| + | |} | ||
| + | |||
| + | == См.также == | ||
| + | *[[Числа Стирлинга второго рода]] | ||
| + | *[[Числа Стирлинга первого рода]] | ||
| + | *[[Числа Эйлера I и II рода]] | ||
==Примeчания== | ==Примeчания== | ||
<references/> | <references/> | ||
| + | |||
| + | ==Источники информации== | ||
| + | *[https://cseweb.ucsd.edu/~gill/BWLectSite/Resources/C1U4SF.pdf Bender Edward A.Williamson, S. Gill, Set Partitions, 319–320, 2006] | ||
| + | * [https://en.wikipedia.org/wiki/Bell_number Wikipedia {{---}}Bell numbers] | ||
| + | *Nobuhiro Izumi Hui-Hsiung "Acta Applicandae Texematicae",79–87.Bell numbers, log-concavity, and log-convexity 2000 | ||
| + | *Aitken A. C. Edinburgh Texematical Notes,18–23 A problem in combinations 1933 | ||
| + | *H. W.BeckerJohn Riordan "The arithmetic of Bell and Stirling numbers" American Journal of Texematics,1948,385–394 | ||
| + | *E. T.Bell Exponential polynomials,Annals of Texematics,1934, 258–277 | ||
| + | *E. T.Bell The iterated exponential integers,Annals of Texematics,1938,539–557 | ||
| + | [[Категория: Дискретная математика и алгоритмы]] | ||
| + | [[Категория: Комбинаторика]] | ||
Текущая версия на 19:40, 4 сентября 2022
| Определение: |
| В комбинаторной математике числа Белла (англ. Bell's numbers) определяют количество возможных способов разбиения множества из элементов на подмножества. |
Числа Белла начинаются с и образуют последовательность:
-й элемент множества чисел Белла, , определяет количество различных способов разбиения множества, то есть количество отношений эквивалентности в нем.
Содержание
Подсчет
Разбиение множества определяется как совокупность попарно непересекающихся подмножеств множества . Например, , потому что множество, состоящее их элементов может быть разделено различными способами:
, т.к. существует только одно возможное разбиение пустого множества. Пустое множество может разбиваться только на само себя. Как было обозначено выше, мы не рассматриваем ни порядок подмножеств, ни порядок элементов в каждом их них. Это означает, что данные разбиения являются идентичными:
В противном случае, если различные упорядочивания множеств считаются различными разбиениями, тогда количество таких упорядоченных разбиений называются упорядоченными числами Белла.
Факторизации
Если число является свободным от квадратов [1], то показывает количество различных мультипликативных разбиений . Если является квадратичным положительным целым числом (является произведением некоторого числа различных простых чисел), то дает число различных мультипликативных разбиений . Это является факторизацией в числа большие, чем (рассматривая две факторизации как идентичные, если они имеют одинаковые факторы в другом порядке.) подтверждает это наблюдение Сильвио Минетоле[2]. Например, является произведением простых чисел , и и имеет факторизаций:
Схемы рифмовки
Числа Белла показывают количество схем рифмовки на строках. Схема рифмы описывает, какие строки рифмуются друг с другом, и поэтому может быть истолковано как отношение экивалентности на множестве строк. Таким образом, возможных четверостиший схемами рифмовки являются: .
Свойства
Формулы суммирования
Биномиальные коэффициенты
Числа Белла удовлетворяют рекуррентному соотношению c участием биномиальных коэффициентов:
Доказательство
Докажем, что По определению число всех неупорядоченных подмножеств -элементного множества. Посчитаем количество неупорядоченных подмножеств для -элементного множества множества: Пусть подмножества множества . Пусть , тогда подмножество множества \ . Пусть , где , тогда можно выбрать способами, а оставшиеся элементы разбить способами. .
Связь с числами Стирлинга второго рода
Другая формула суммирования представляет каждое число Белла как сумму чисел Стирлинга второго рода:
- ,
где число Стирлинга является количеством способов разбиения набора элементов в ровно непустых подмножеств.
Доказательство
Посчитаем количество подмножеств -элементного множества. Нам нужно разбить -элементное множество на непустых подмножеств, где от до . Пусть все подмножества -элементного множества. Пусть разбиение -элементного множества на непустых подмножеств, тогда . по определению, тогда , т.к. .
Объединяющая формула
Майкл Спайви[3] получил формулу, которая объединяет оба эти суммирования:
Лемма
количество способов разбить -элементное множество на подмножества. Количество способов разбить -элементное множество на непустых подмножеств это , где меняется от до . Из оставшихся объектов выберем , для разделения их на новые подмножества, а оставшиеся объектов распределим между подмножествами, сформированных из -элементного множества. количество разбиений -элементного множества на подмножества и способов разбить элементов между подмножествами. Значит способов разбить элементов на подмножеств и выбрать элементов из -элементного множества и выбрать элементов из -элементного множества и сформировать из них новые подмножества, а из оставшихся объектов разделить между множествами, сформированных из -элементного множества.
Доказательство
Суммируя подмножества, рассмотренные в лемме, меняя и , получаем: т.к. .
Производящая функция
Экспоненциальной производящей функцией чисел Белла является:
Суммирование используется для определения экспоненциальной производящей функции для любой последовательности чисел. Правая часть является результатом выполнения суммирования в конкретном случае.
Моменты распределения вероятностей
Числа Белла удовлетворяют формуле Добинского:
Эта формула может быть получена за счет расширения экспоненциальной производящей функции, используя ряд Тейлора[4] для экспоненциальной функции, а затем собирая условия с аналогичным показателем экспоненты.[5]. Это позволяет интерпретировать Bn как -й момент Пуассоновского распределения с ожидаемым значением .
Интегральное представление
Применение интегральной формулы Коши [6] для экспоненциальной производящей функции дает комплексное интегральное представление:
Логарифмическая вогнутость
Числа Белла формируют логарифмически выпуклую последовательность. Деление их на факториал, , дает логарифмически выпуклую последовательность.
Темпы роста
Известно несколько асимптотических формул для чисел Белла. Беренд Тасса в -м[7] установлил следующие границы:
- для всех положительных чисел ;
кроме того, если затем для всех ,
где и Числа Белла могут быть аппроксимированы с помощью функции Ламберта [8], данная функция имеет такой же темп роста, как логарифм, как
Мозер Л. и Вайман М.[9] установили расширение:
Асимптотическое выражение
Было установлено де Брайном[10] в году.
Получение
Вычисление с помощью треугольника Пирса
Числа Белла могут быть с легкостью вычислены с помощью треугольника Белла, который также называют массивом Айткена или треугольником Пирса.
- Начнем с единицы. Помещаем ее в верхнюю строку. ()
- Каждая новая строка должна начинаться с крайнего правого элемента прошлой строки. ()
- Заполняем строчку по формуле , начиная с , пока .
- Крайнее левое число данной строки является числом Белла для этой строки. ()
Первые пять строк треугольника, построенного по этим правилам:
Получение с помощью чисел Стирлинга второго рода
Числа Стирлинга второго рода связаны друг с другом по следующей формуле: Число Стирлинга второго рода показывает количество способов разбиения множества из элементов на непустых подмножеств. Если сложить все числа Стирлинга второго рода, имеющих одинаковую , то получим количество способов разбиения множества из элементов на непустых подмножеств, то есть -ое число Белла.
Заполним таблицу чисел Стирлинга, используя формулу выше. Cумма чисел -ой строки будет являться -ым числом Белла.
| n \ k | Число Белла | |||||
См.также
Примeчания
- ↑ Wikipedia — Cвободные от квадратов числа
- ↑ Williams 1945 credits this observation to Silvio Minetola's Principii di Analisi Combinatoria (1909).
- ↑ Spivey, Michael Z. (2008). "A generalized recurrence for Bell numbers" . Journal of Integer Sequences. 11 (2): Article 08.2.5, 3. MR 2420912.
- ↑ Ряд Тейлора
- ↑ Flajolet & Sedgewick (2009)
- ↑ Формула Коши
- ↑ Berend, D.; Tassa, T. (2010). "Improved bounds on Bell numbers and on moments of sums of random variables". Probability and Mathematical Statistics. 30 (2): 185–205.
- ↑ Функция Ламберта W
- ↑ Moser, Leo; Wyman, Max (1955). "An asymptotic formula for the Bell numbers". Transactions of the Royal Society of Canada, Section III.
- ↑ de Bruijn, N.G. (1981). Asymptotic methods in analysis (3rd ed.). Dover. p. 108.
Источники информации
- Bender Edward A.Williamson, S. Gill, Set Partitions, 319–320, 2006
- Wikipedia —Bell numbers
- Nobuhiro Izumi Hui-Hsiung "Acta Applicandae Texematicae",79–87.Bell numbers, log-concavity, and log-convexity 2000
- Aitken A. C. Edinburgh Texematical Notes,18–23 A problem in combinations 1933
- H. W.BeckerJohn Riordan "The arithmetic of Bell and Stirling numbers" American Journal of Texematics,1948,385–394
- E. T.Bell Exponential polynomials,Annals of Texematics,1934, 258–277
- E. T.Bell The iterated exponential integers,Annals of Texematics,1938,539–557