Числа Эйлера I и II рода — различия между версиями
VolhovM (обсуждение | вклад) (→Пример) |
VolhovM (обсуждение | вклад) |
||
| Строка 62: | Строка 62: | ||
==Треугольник чисел Эйлера I рода и явная формула== | ==Треугольник чисел Эйлера I рода и явная формула== | ||
| + | |||
| + | ===Явная формула=== | ||
| + | Приведем также без вывода явную формулу для вычисления чисел Эйлера I рода: | ||
| + | |||
| + | <tex dpi = "180">\left\langle{n\atop m}\right\rangle = \sum_{k=0}^{m}[ (-1)^k {n+1\choose k} (m+1-k)^n]</tex> | ||
| + | |||
| + | |||
| + | ===Треугольник чисел Эйлера I рода=== | ||
| + | На значениях <tex dpi = "130">n = m</tex> чисел Эйлера I рода можно построить массив <tex dpi = "130">n \times m</tex>, нижнедиагональная часть которого названа треугольником чисел Эйлера I рода. | ||
| + | |||
| + | ::{| class="number_triangle" | ||
| + | |||
| + | |- align="center" | ||
| + | | style="background:white; color:black; width:50px;" | | ||
| + | | style="background:white; color:black; width:50px;" | '''''k = 0''''' | ||
| + | | style="background:white; color:black; width:50px;" | '''''1''''' | ||
| + | | style="background:white; color:black; width:50px;" | '''''2''''' | ||
| + | | style="background:white; color:black; width:50px;" | '''''3''''' | ||
| + | | style="background:white; color:black; width:50px;" | '''''4''''' | ||
| + | | style="background:white; color:black; width:50px;" | '''''5''''' | ||
| + | | style="background:white; color:black; width:50px;" | '''''6''''' | ||
| + | | style="background:white; color:black; width:50px;" | '''''7''''' | ||
| + | | style="background:white; color:black; width:50px;" | '''''8''''' | ||
| + | | style="background:white; color:black; width:50px;" | '''''9''''' | ||
| + | | style="background:white; color:black; width:50px;" | '''''10''''' | ||
| + | | style="background:white; color:black; width:50px;" | '''''11''''' | ||
| + | | style="background:white; color:black; width:50px;" | '''''12''''' | ||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''n = 0''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''1''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''2''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''3''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''4''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''4''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''11''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''11''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''5''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''26''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''66''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''26''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''6''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''57''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''302''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''302''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''57''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''7''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''120''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1191''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''2416''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1191''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''120''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''8''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''247''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''4293''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''15619''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''15619''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''4293''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''247''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''9''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''502''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''14608''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''88234''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''156190''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''88234''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''14608''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''502''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''10''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1013''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''47840''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''455192''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1310354''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1310354''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''455192''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''47840''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1013''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''11''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''2036''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''152637''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''2203488''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''9738114''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''15724248''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''9738114''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''2203488''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''152637''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''2036''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |- align="center" | ||
| + | | style="background:white; color:black;" | '''''12''''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''4083''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''478271''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''10187685''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''66318474''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''162512286''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''162512286''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''66318474''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''10187685''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''478271''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''4083''' | ||
| + | | style="background:#FFDEAD; color:black;" | '''1''' | ||
| + | | style="background:#FFDEAD; color:red;" | '''0''' | ||
| + | |} | ||
| + | |||
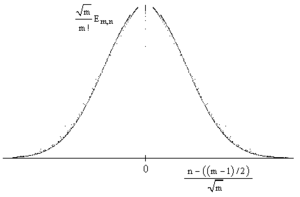
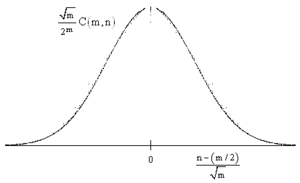
| + | Стоит отметить, что гистрограмма, построенная на значениях чисел Эйлера I рода аппроксимируется к гистограмме, построенной на биноминальных коээфициентах (оба графика, представленные '''справа''', смасштабированы; масштаб указан на гистограмме): | ||
| + | [[Файл:Euler_I_hist.gif|300px|thumb|right|Числа Эйлера I рода (m < 90)]] | ||
| + | [[Файл:Binomial_hist.gif|300px|thumb|right|Биномиальные коээфициенты (m < 60)]] | ||
| + | |||
| + | '''Полезные факты о числах Эйлера I рода''' | ||
| + | 1. Нетрудно увидеть, что каждый ряд ненулевых значений симметричен относительно своей середины, то есть: | ||
| + | :<tex dpi = "160">\left\langle{n\atop m}\right\rangle = \left\langle{n\atop (n-1) - k}\right\rangle,\ n \ge 1,\ 0 \le k \le n-1. \, </tex> | ||
| + | |||
| + | 2. Сумма всех значений каждого ряда равна <tex dpi = "130"> n! </tex>: | ||
| + | :<tex dpi = "160">\sum_{k=0}^{n} \left\langle{n\atop m}\right\rangle = n!,\ n \ge 0, \,</tex> | ||
| + | |||
| + | 3. <tex dpi = "160">\sum_{m=0}^n (-1)^m {\left\langle{n\atop m}\right\rangle}{n-1\choose m}^{-1}=0.</tex> | ||
==Числа Эйлера II рода== | ==Числа Эйлера II рода== | ||
Версия 00:32, 19 декабря 2013
Числа Эйлера I рода (Eulerian numbers) — количество перестановок чисел от 1 до n таких, что в каждой из них существует ровно m подъемов. Числа Эйлера I рода обозначают как или же .
| Определение: |
| Пусть и - элементы некоторой перестановки порядка причем . Тогда пара называется подъемом (ascent) данной перестановки. |
Содержание
Вывод рекуррентной формулы
Пусть у нас есть некая перестановка . Тогда операцией вставки элемента с номером n в какую-либо из позиций мы получим перестановок вида . Далее рассмотрим два случая:
1. Количество подъемов в перестановке равно количеству подъемов в . Этого можно добиться, вставляя элемент на самое первое место в (всего возможностей) или перед последним последним элементом каждого подъема(еще раз).
2. Количество подъемов в новой перестановке на один больше предыдущего количества. Этого эффекта добиваемся вставкой элемента в конце каждой перестановки или после элемента перестановки со значением . Таких элементов, как не трудно догадаться, будет .
Тогда рекуррентная формула имеет вид:
Примем также следующие начальные значения:
, если или если ;
Пример
Рассмотрим все перестановки порядка , в которых есть ровно 2 подъема (в квадратных скобках один или больше подъемов подряд):
Согласно алгоритму вывода рекуррентной формулы мы можем добавить '4' в следующие позиции всех перестановок порядка с двумя подъемами, не увеличив количество подъемов:
Далее рассмотрим все перестановки порядка с одним подъемом, причем операцией вставки мы будем увеличивать количество перестановок на 1:
Таким образом мы убеждаемся в верности формулы:
Треугольник чисел Эйлера I рода и явная формула
Явная формула
Приведем также без вывода явную формулу для вычисления чисел Эйлера I рода:
Треугольник чисел Эйлера I рода
На значениях чисел Эйлера I рода можно построить массив , нижнедиагональная часть которого названа треугольником чисел Эйлера I рода.
k = 0 1 2 3 4 5 6 7 8 9 10 11 12 n = 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 2 1 1 0 0 0 0 0 0 0 0 0 0 0 3 1 4 1 0 0 0 0 0 0 0 0 0 0 4 1 11 11 1 0 0 0 0 0 0 0 0 0 5 1 26 66 26 1 0 0 0 0 0 0 0 0 6 1 57 302 302 57 1 0 0 0 0 0 0 0 7 1 120 1191 2416 1191 120 1 0 0 0 0 0 0 8 1 247 4293 15619 15619 4293 247 1 0 0 0 0 0 9 1 502 14608 88234 156190 88234 14608 502 1 0 0 0 0 10 1 1013 47840 455192 1310354 1310354 455192 47840 1013 1 0 0 0 11 1 2036 152637 2203488 9738114 15724248 9738114 2203488 152637 2036 1 0 0 12 1 4083 478271 10187685 66318474 162512286 162512286 66318474 10187685 478271 4083 1 0
Стоит отметить, что гистрограмма, построенная на значениях чисел Эйлера I рода аппроксимируется к гистограмме, построенной на биноминальных коээфициентах (оба графика, представленные справа, смасштабированы; масштаб указан на гистограмме):
Полезные факты о числах Эйлера I рода 1. Нетрудно увидеть, что каждый ряд ненулевых значений симметричен относительно своей середины, то есть:
2. Сумма всех значений каждого ряда равна :
3.