Эквивалентность состояний ДКА — различия между версиями
Lidia2008 (обсуждение | вклад) (→Эквивалентность автоматов) |
Lidia2008 (обсуждение | вклад) (→Эквивалентность автоматов) |
||
| Строка 5: | Строка 5: | ||
*'''Определение: ''' Два <em> автомата</em> <tex>\mathcal{A}_1(Q_1,\Sigma,\delta_1,s_10, T_1\subseteq Q_1)</tex> и <tex>\mathcal{A}_2(Q_2,\Sigma,\delta_2,s_20, T_2\subseteq Q_2)</tex> называются <em>эквивалентными</em>, если они распознают один и тот же язык над алфавитом <tex>\Sigma</tex>. | *'''Определение: ''' Два <em> автомата</em> <tex>\mathcal{A}_1(Q_1,\Sigma,\delta_1,s_10, T_1\subseteq Q_1)</tex> и <tex>\mathcal{A}_2(Q_2,\Sigma,\delta_2,s_20, T_2\subseteq Q_2)</tex> называются <em>эквивалентными</em>, если они распознают один и тот же язык над алфавитом <tex>\Sigma</tex>. | ||
| − | *'''Определение: ''' Два <em> состояния</em> <tex> | + | *'''Определение: ''' Два <em> состояния</em> <tex>q_i</tex> и <tex>q_j</tex> называются <em>эквивалентными</em> <tex>(q_i \sim q_j)</tex>, если <tex>\forall z\in \Sigma^*</tex> верно, что <tex>\delta(q_i, z)\in T \Leftrightarrow \delta(q_j, z)\in T</tex>. Из этого следует, что если два состояния <tex>q_i</tex> и <tex>q_j</tex> эквивалентны, то и состояния <tex>\delta_1(q_i, a)</tex> и <tex>\delta_2(q_j, a)</tex> будут эквивалентными для <tex>\forall a \in \Sigma</tex>. Кроме того, т.к. переход <tex>\delta(q, \varepsilon)</tex> может возникнуть только для конечного состояния <tex>q</tex>, то никакое допускающее(терминальное) состояние не может быть эквивалентно не допускающему состоянию. Нахождение классов эквивалентных состояний внутри автомата и их совмещение в одно состояние используется в быстром алгоритме Хопкрофта для минимизации автомата, работающий за <tex>O(n \log n)</tex>. |
| − | *'''Определение:''' Слово <tex>z \in \Sigma^*</tex> различает два состояния <tex>( | + | *'''Определение:''' Слово <tex>z \in \Sigma^*</tex> различает два состояния <tex>(q_i \nsim q_j)</tex>, если <tex>\delta(q_i, z)\in T \Leftrightarrow \delta(q_j, z)\notin T</tex>. Также, если слово <tex>z</tex> различает состояния <tex>t_1</tex> и <tex>t_2</tex> такие, что <tex>t_1=\delta(q_1, a)</tex> и <tex>t_2=\delta(q_2, a)</tex>, то слово <tex>aw</tex> различает состояния <tex>q_1</tex> и <tex>q_2</tex>. Нахождение пар различных состояний в автомате используется в алгоритме минимизации автомата, работающий за <tex>O(n^2)</tex>. |
*'''Пример двух эквивалентных автоматов:''' | *'''Пример двух эквивалентных автоматов:''' | ||
| − | [[Изображение:Automata1.png]][[Изображение:Automata2.png]] | + | [[Изображение:Automata1.png]][[Изображение:Automata2.png]] |
| + | |||
| + | <em>Состояния <tex>B</tex> и <tex>C</tex> допускающие.</em> | ||
| + | |||
| + | </font> | ||
| + | == Проверка эквивалентности автоматов == | ||
| + | |||
| + | <font face="Times" size="3"> | ||
| + | *Если положить, что начальные состояния эквивалентны, то последовательно, переходя по одному символу из состояний, можем получить и другие пары эквивалентных состояний. Если же в одну из таких пар попадут допускающее состояния вместе с не допускающим, то такие <tex>q_i</tex> и <tex>q_j</tex> неэквивалентны. | ||
| + | <tex> | ||
| + | AlgoPartition(Q_1, Q_2, q_{10}, q_{20}) | ||
| + | { | ||
| + | } | ||
| + | </tex> | ||
</font> | </font> | ||
Версия 22:30, 2 октября 2010
Эквивалентность автоматов
- Определение: Два автомата и называются эквивалентными, если они распознают один и тот же язык над алфавитом .
- Определение: Два состояния и называются эквивалентными , если верно, что . Из этого следует, что если два состояния и эквивалентны, то и состояния и будут эквивалентными для . Кроме того, т.к. переход может возникнуть только для конечного состояния , то никакое допускающее(терминальное) состояние не может быть эквивалентно не допускающему состоянию. Нахождение классов эквивалентных состояний внутри автомата и их совмещение в одно состояние используется в быстром алгоритме Хопкрофта для минимизации автомата, работающий за .
- Определение: Слово различает два состояния , если . Также, если слово различает состояния и такие, что и , то слово различает состояния и . Нахождение пар различных состояний в автомате используется в алгоритме минимизации автомата, работающий за .
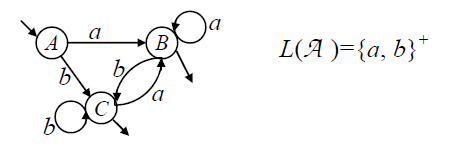
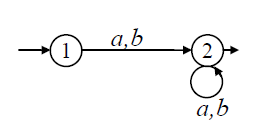
- Пример двух эквивалентных автоматов:
Состояния и допускающие.
Проверка эквивалентности автоматов
- Если положить, что начальные состояния эквивалентны, то последовательно, переходя по одному символу из состояний, можем получить и другие пары эквивалентных состояний. Если же в одну из таких пар попадут допускающее состояния вместе с не допускающим, то такие и неэквивалентны.