Heavy-light декомпозиция — различия между версиями
| Строка 54: | Строка 54: | ||
Задача о наименьшем общем предке для двух вершин в дереве с <tex>n</tex> вершинами решается с помощью Heavy-light декомпозиции за время <tex>O(\log{n})</tex>. | Задача о наименьшем общем предке для двух вершин в дереве с <tex>n</tex> вершинами решается с помощью Heavy-light декомпозиции за время <tex>O(\log{n})</tex>. | ||
| − | Мы можем проверять, что вершина является предком другой вершины за <tex>O(1)</tex> с помощью времен входа\выхода в каждую вершину. Тогда рассмотрим самый нижний путь (содержащий первую вершину) и посмотрим на его корень (самая высокая вершина в пути). Если эта вершина является предком второй вершины, то ответ где-то в этом пути, иначе | + | Мы можем проверять, что вершина является предком другой вершины за <tex>O(1)</tex> с помощью времен входа\выхода в каждую вершину. Тогда рассмотрим самый нижний путь (содержащий первую вершину) и посмотрим на его корень (самая высокая вершина в пути). Если эта вершина является предком второй вершины, то ответ где-то в этом пути, иначе рассмотрим следующий сверху путь. |
Когда мы определили путь, в котором содержится ответ, мы можем с помощью бинпоиска найти в нём первую вершину, являющуюся предком второй вершины. Эта вершина является ответом. | Когда мы определили путь, в котором содержится ответ, мы можем с помощью бинпоиска найти в нём первую вершину, являющуюся предком второй вершины. Эта вершина является ответом. | ||
Версия 23:38, 8 июня 2015
Heavy-light декомпозиция — техника разбиения подвешенного дерева на множество путей для решения задач о запросах на пути в дереве (в том числе с модификациями).
Содержание
Описание задачи
| Задача: |
| Имеется подвешенное дерево c вершинами и необходимо проводить операции на нем на пути от вершины до вершины . |
Примеры запросов:
- сумма на пути,
- максимум на пути,
- количество рёбер на пути, вес которых больше заданного .
Примеры модификаций:
- модификация одного ребра,
- прибавление к весу всех рёбер на пути,
- установка веса всех рёбер на пути в заданное .
Множество подобных запросов делаются за время за полином от логарифма (обычно ) с помощью Heavy-light декомпозиции.
Описание декомпозиции
Необходимо составить такую декомпозицию дерева на множество рёберно-непересекающихся путей, что при прохождении от одной вершины до другой произойдет смена не более путей из декомпозиции.
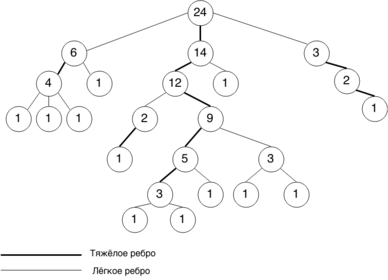
Декомпозиция заключается в классификации всех рёбер дерева в 2 вида: легкие и тяжёлые. Введём функцию , которая будет обозначать размер поддерева вершины .
Тяжёлые ребра (англ. heavy edge) — ребра такие, что .
Лёгкие ребра (англ. light edge) — соответственно все остальные.
Очевидно, что из вершины может выходить как максимум одно тяжёлое ребро, т.к. иначе у нас есть два поддерева по как минимум вершин, а также сама вершина . Итого вершин, тогда как у нас всего вершин в поддереве.
Теперь рассмотрим вершины, из которых не ведет вниз ни одно тяжёлое ребро. Будем идти от них вверх до корня или пока не пройдем легкое ребро. Получится какое-то множество путей. Утверждается, что полученная таким образом декомпозиция будет являться искомой и корректной.
| Утверждение: |
Полученная декомпозиция является искомой. |
|
Докажем по отдельности корректность декомпозиции.
|
Существует вариант Heavy-light декомпозиции на вершинно-непересекающихся путях. Чтобы получить такой путь нужно всего-лишь выкинуть последнее ребро из всех путей в рёберно-непересекающейся декомпозиции. Это может быть удобно при решении задач, где веса находятся не на рёбрах, а на вершинах и соответствующие запросы также делаются на вершинах.
Применение
Сумма на пути
Классическая задача о сумме на пути в дереве с вершинами решается с помощью Heavy-light декомпозиции за время . Возможны модификации веса.
Построим дерево отрезков над каждым путём. Рассмотрим запрос . Найдем вершину , которая является (например с помощью двоичного подъема. Мы разбили запрос на два: и , на каждый из которых можно легко ответить разбив его на множество путей из декомпозиции и ответив на каждый путь из этого множества по отдельности за с помощью дерева отрезков на этом пути. Всего таких путей нужно будет рассмотреть . Итого мы способны решить эту задачу за время .
Хоть это и не самый эффективный способ для решения этой задачи, но можно заметить, что навесив дерево отрезков на каждый путь мы способны отвечать на любые операции, определяемые на множестве, на котором данная операция ассоциативна, и существует нейтральный элемент относительно этой операции, то есть на моноиде (операции, поддерживаемые деревом отрезков), такие как: сумма на пути, максимум на пути, количество рёбер на пути, удовлетворяющих какому-то свойству.
LCA
Задача о наименьшем общем предке для двух вершин в дереве с вершинами решается с помощью Heavy-light декомпозиции за время .
Мы можем проверять, что вершина является предком другой вершины за с помощью времен входа\выхода в каждую вершину. Тогда рассмотрим самый нижний путь (содержащий первую вершину) и посмотрим на его корень (самая высокая вершина в пути). Если эта вершина является предком второй вершины, то ответ где-то в этом пути, иначе рассмотрим следующий сверху путь.
Когда мы определили путь, в котором содержится ответ, мы можем с помощью бинпоиска найти в нём первую вершину, являющуюся предком второй вершины. Эта вершина является ответом.
Итого мы рассмотрели корень каждого пути за , а путей всего . И в последнем пути один раз запустили бинпоиск, который отработал за . Итоговая асимптотика .
Реализация
Ниже будет приведена реализация запроса сумма на пути между любыми двумя вершинами в дереве без запросов модификации. Все запросы, сводящиеся к навешиванию дерева отрезков на пути из декомпозиции делаются похожим образом.
Опущены некоторые детали реализации: построение и дерево отрезков.
- — функция, позволяющая найти смещение вершины в пути относительно корня пути,
- — функция, позволяющая найти вес -ого ребра в -ом пути.
Пример реализации запроса суммы на пути:
int query(int u, int v):
int res = 0
int root = корень пути, в котором находится u
while root не является предком v // поднимаемся до тех пор, пока наш путь не содержит общего предка u и v
segmentTree = дерево отрезков, соответствующее путю в котором лежит u
res += segmentTree.sum(0, pathPos(u))
u = предок root // вырезали нижний путь и подняли нижнюю вершину до нижней вершины следующего пути
root = корень пути, в котором находится u
root = корень пути, в котором находится v
while root не является предком u // аналогично прошлому while, но с другой стороны
segmentTree = дерево отрезков, соответствующее пути в котором лежит v
res += segmentTree.sum(0, pathPos(v))
v = предок root
root = корень пути, в котором находится v
// последний путь (тот, что содержит общего предка) обрезан с двух сторон полученными вершинами
segmentTree = дерево отрезков, соответствующее пути в котором лежит u
res += segmentTree.sum(min(pathPos(u), pathPos(v)), max(pathPos(u), pathPos(v)))
return res