List order maintenance
List order maintance (русск. поддержка порядка в списке) — проблема поддержки списка со следующими операциями:
- — вставка нового элемента в список сразу после ;
- — удаление элемента из списка;
- — команда, возвращающая , если в списке находится до и иначе.
Существует реализация структуры, где все операции выполняются за амортизационную . Список с командой порядка используется в разных алгоритмах и структурах, к примеру, в реализации полностью персистентного дерева поиска.
Содержание
Алгоритм за O(logn)
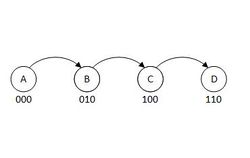
Рассмотрим реализацию списка с командой порядка, где все операции выполняются за амортизационную . Дадим каждому элементу списка метки длины из битов. Пусть , где — количество элементов в списке. Если после добавления или удаления элементов перестанет удовлетворять неравенству, пересчитаем все метки заново. Пересчет меток занимает амортизационно по аналогии с саморасширяющимся массивом. Пусть метки идут по возрастанию от начала к концу списка. Опишем взаимодействие с метками при выполнении операций:
- операция порядка: можно сделать, просто сравнив метки за (так как они идут по возрастанию);
- удаление вершины: для выполнения просто удалим элемент вместе с его меткой за , проверим, удовлетворяет ли неравенству, если нет — пересчитаем;
- добавление вершины: для существуют два возможных случая:
- есть свободная метка: проверим, есть ли между элементом и следующим за ним элементом свободная метка. Если есть, дадим любую свободную метку между ними. После этого опять проверим на соответствие неравенству.
- свободной метки нет: В случае, если между и следующим за ним элементом свободной метки нет, нам придется пересчитать метки описанным ниже способом.
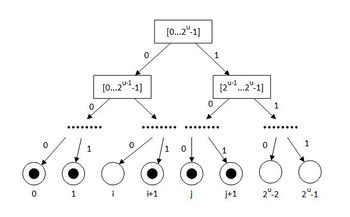
Способ хранения меток. Все метки хранятся в цифровом боре высоты (там хранятся не только используемые метки, а вообще все возможные заданной длины). В узлах будем хранить:
- в листьях будем хранить, используется ли уже эта метка. Пусть — это количество помеченных (используемых) листьев (меток) в поддереве , а — это количество всех листьев в поддереве ;
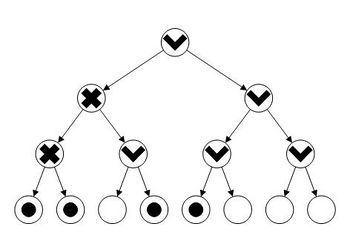
- в нелистовых узлах будем хранить, является ли узел переполненным. Для любой будем считать, что узел дерева переполнен, если . Стоит заметить, что все листья всегда непереполнены. В худшем случае: . Получается, что, чем выше, тем более разреженными должны быть поддеревья непереполненных узлов.
Перераспределение меток. Тогда, как только мы получаем команду вставить элемент, которому не хватает метки, мы поднимаемся вверх от метки элемента , пока не найдем первый непереполненный узел. Может случиться такое, что на всем пути до корня мы не найдем ни одного непереполненного узла. Чтобы этого избежать, изменим требования к позже. Как только мы нашли первый непереполненный узел, переназначим метки в его поддереве так, чтобы они находились друг от друга на одинаковых расстояниях (места точно хватит, так как , если узел непереполненный). После этого плотность распределения всех занятых листьев составит примерно .
Докажем амортизационную стоимость операции добавления.
- С одной стороны, повторное перераспределение меток в поддереве узла потребуется, когда сын этого узла снова переполнится. Если — сын , то он переполнится, когда . Чтобы это произошло, требуется, чтобы было сделано еще добавлений.
- С другой стороны, следующее переспределение меток произойдет, когда . Получается, что за операций перераспределения меток требуется сделать операций добавления.
Тогда если за каждую операцию добавления брать монет, то за добавления накопится столько монет, чтобы расплатиться за следующую операцию перераспределения в узле . Проблема в том, что таким образом надо платить за каждый уровень, а количество уровней (бит) равно . Тогда амортизированная стоимость добавления .
Теперь выберем такое , чтобы корень никогда не переполнялся: . Тогда операция добавления работает за .
Алгоритм за O(1)
Предыдущий алгоритм работает за логарифм из-за того, что слишком часто приходится делать перераспределение меток. Используем (модифицированный цифровой бор), чтобы улучшить время работы операции добавления до .
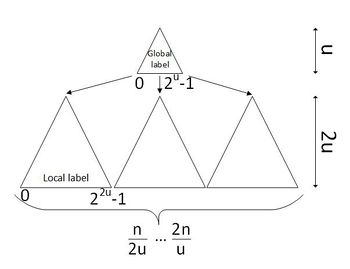
У каждого элемента списка будет две метки: глобальная и локальная. Глобальная задает блок, локальная — положение элемента внутри блока. Описание взаимодействия с метками:
- локальные метки внутри каждого блока будем присваивать каждому элементу от до жадно. Стоит заметить, что внутри блока никогда не будет проблемы, что кому-то не хватит метки или придется сделать перераспределение меток, так как, если мы каждый раз в качестве метки будем брать среднее значение, то для того, чтобы был конфликт из-за меток, нужно больше, чем ключей (противоречит условию);
- глобальные метки будут организованы в структуру, использовавшуюся в реализации операции за логарифмическое время. Глобальные метки для блоков нам придется менять, когда один из блоков переполнился. Тогда разделим блок на два, присвоив метку второму, методом, описанным выше (поднимемся до первого непереполненного). Каждый блок будет иметь занятых меток. Аналогично, когда в каком-то блок становится слишком мало ключей, мы его сливаем с соседним.
Внутри блоков мы присваиваем ключи за , а, аналогичный приведенному выше анализ показывает, что, чтобы потребовалось перераспределение глобальных меток, требуется изменений локальных меток. За эти изменения накопим монет для изменения глобальных меток, тогда операция добавления работает за константное время.
Использование памяти
Из-за того, что зависит от выбранной , сильно влияет на реализацию. Увеличивая , мы уменьшаем стоимость операции добавления (количество монет, которые надо брать: ), но увеличиваем , значит, требуется больше памяти, а, уменьшая , мы выигрываем в памяти, но проигрываем во времени операции добавления. Так как для реализации структуры мы используем , требуется памяти.
Послесловие
Впервые реализацию такой структуры данных со всеми операциями за константное время амортизационно предложили[1] Dietz и Sleator, однако их доказательство времени работы было намного сложнее вышеизложенного анализа. Поэтому позже группа ученых во главе с Michael A. Bender разработала[2] более простое доказательство, изложенное выше, впервые описанное в их статье Two simlified algorithms for maintaining order in a list. Послесловие их статьи таково:
Dietz and Sleator is quite influential With its tags and its proofs by potential But to teach it in class Is a pain in the ass So our new result is preferential.