PpmtnriLmax — различия между версиями
Proshev (обсуждение | вклад) |
(→Решение) |
||
| (не показано 12 промежуточных версий 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | = | + | <tex dpi = "200">P \mid pmtn, r_i \mid L_{max}</tex> |
| − | + | {{Задача | |
| − | + | |definition = <ol> | |
| − | + | <li>Имеется <tex>M</tex> однородных машин, работающих параллельно.</li> | |
| + | <li>Есть <tex>n</tex> работ, каждое имеет своё время появления <tex>r_i</tex> и время окончания <tex>d_i</tex>.</li> | ||
| + | <li>Работа может быть прервана и продолжена позже.</li> | ||
| + | </ol> | ||
| − | Необходимо составить такое расписание, чтобы значение <tex>L_{max} = | + | Необходимо составить такое расписание, чтобы значение <tex>L_{max} = \max\limits_{i=1\ldots n} (C_i - d_i)</tex> было минимальным.}} |
== Решение == | == Решение == | ||
| − | + | [[Файл:Figure_5.2.png|400px|thumb|right|Рис. 1. Cеть]] | |
Сведем эту задачу к поиску максимального потока в сети, построенной указанным ниже образом. | Сведем эту задачу к поиску максимального потока в сети, построенной указанным ниже образом. | ||
| Строка 15: | Строка 18: | ||
Пусть <tex>t_1 < t_2 < \ldots < t_r</tex> - упорядоченная последовательность <tex>r_i</tex> и <tex>d_i</tex>. Определим интервалы <tex>I_K = [t_K; t_{K+1}]</tex> с длиной <tex>T_K = t_{K+1} - t_K</tex> для всех <tex>K = 1 \ldots r-1</tex>. | Пусть <tex>t_1 < t_2 < \ldots < t_r</tex> - упорядоченная последовательность <tex>r_i</tex> и <tex>d_i</tex>. Определим интервалы <tex>I_K = [t_K; t_{K+1}]</tex> с длиной <tex>T_K = t_{K+1} - t_K</tex> для всех <tex>K = 1 \ldots r-1</tex>. | ||
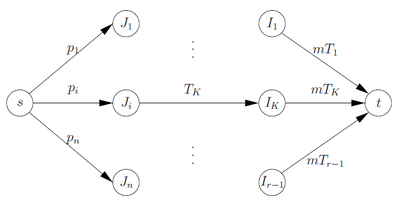
| − | Работам сопоставим свой тип вершин, а интервалам <tex>I_K</tex> свой. Добавим две фиктивные вершины <tex>s</tex> и <tex>t</tex>. | + | Работам <tex>J_i</tex> сопоставим свой тип вершин, а интервалам <tex>I_K</tex> свой. Добавим две фиктивные вершины <tex>s</tex> и <tex>t</tex>. Вершина <tex>s</tex> соединена с вершинами <tex>J_i</tex> ребрами с пропускной способностью <tex>p_i</tex>, вершина <tex>t</tex> соединена с вершинами <tex>I_K</tex> ребрами с пропускной способностью <tex>mT_K</tex>. Ребро между вершиной <tex>J_i</tex> и вершиной <tex>I_K</tex> существует, если <tex>r_i \leqslant t_K, t_{K+1} \leqslant d_i</tex>. Пропускная способность этого ребра - <tex>T_K</tex>. |
| + | |||
| + | Нетрудно понять, что расписание существует, если максимальный поток через эту сеть равен <tex>\sum\limits_{i=1}^n p_i</tex>. | ||
| + | |||
| + | Если это так, то поток <tex>x_{iK}</tex> на дуге <tex>(J_i, I_K)</tex> соответствует тому, что работа <tex>J_i</tex> будет выполняться во временном интервале <tex>I_K</tex>, и будет справедливо следующее: | ||
| + | |||
| + | # <tex>\sum\limits_{K=1}^{r-1} x_{iK} = p_i, i = 1 \ldots n</tex> | ||
| + | # <tex>\sum\limits_{i=1}^n x_{iK} \leqslant mT_K, K = 1 \ldots r - 1</tex> | ||
| + | # <tex>x_{iK} \leqslant T_K</tex> для всех ребер <tex>(J_i, I_K)</tex> | ||
| + | |||
| + | Исходя из этого, расписание строится выполнением работы <tex>J_{iK}</tex> с временем выполнения <tex>x_{iK} > 0</tex> в интервале <tex>I_K</tex>. | ||
| + | |||
| + | Т.к. сеть содержит <tex>O(n)</tex> элементов, значит максимальный поток в ней можно найти за <tex>O(n^3)</tex>. Кроме того, построение "окон" выполнения работ займет <tex>O(n^2)</tex>. Т.о. указанный выше алгоритм потребует <tex>O(n^3)</tex> операций. | ||
| + | |||
| + | Для решения данной задачи мы используем бинпоиск по <tex>L</tex> значениям, а значит, получаем алгоритм с <tex>\varepsilon</tex>-приближенной сложностью <tex>O (n^3(\log(n) + \log(\cfrac{1}{\varepsilon}) + \log(\max\limits_{j=1 \ldots n} (p_j))) </tex>, потому как <tex>L_{max}</tex>, ограничен <tex>n\max\limits_{j=1 \ldots n} (p_j)</tex> | ||
| + | |||
| + | [[Категория: Алгоритмы и структуры данных]] | ||
| + | [[Категория: Теория расписаний]] | ||
Версия 01:02, 14 июня 2015
| Задача: |
|
Решение
Сведем эту задачу к поиску максимального потока в сети, построенной указанным ниже образом.
Пусть - упорядоченная последовательность и . Определим интервалы с длиной для всех .
Работам сопоставим свой тип вершин, а интервалам свой. Добавим две фиктивные вершины и . Вершина соединена с вершинами ребрами с пропускной способностью , вершина соединена с вершинами ребрами с пропускной способностью . Ребро между вершиной и вершиной существует, если . Пропускная способность этого ребра - .
Нетрудно понять, что расписание существует, если максимальный поток через эту сеть равен .
Если это так, то поток на дуге соответствует тому, что работа будет выполняться во временном интервале , и будет справедливо следующее:
- для всех ребер
Исходя из этого, расписание строится выполнением работы с временем выполнения в интервале .
Т.к. сеть содержит элементов, значит максимальный поток в ней можно найти за . Кроме того, построение "окон" выполнения работ займет . Т.о. указанный выше алгоритм потребует операций.
Для решения данной задачи мы используем бинпоиск по значениям, а значит, получаем алгоритм с -приближенной сложностью , потому как , ограничен