RSA — различия между версиями
(→Реализация) |
|||
| Строка 45: | Строка 45: | ||
* Взять открытый текст <tex>m</tex> | * Взять открытый текст <tex>m</tex> | ||
* Зашифровать сообщение с использованием открытого ключа Алисы: | * Зашифровать сообщение с использованием открытого ключа Алисы: | ||
| − | *: <tex>c = E(m) = m^e \mod n </tex> | + | *: <tex>c = E(m) = m^e \mod n ~~~~ (1)</tex> |
[[Файл:Gg1.png|800px|center]] | [[Файл:Gg1.png|800px|center]] | ||
| Строка 54: | Строка 54: | ||
* Взять свой закрытый ключ <tex>(d,n)</tex> | * Взять свой закрытый ключ <tex>(d,n)</tex> | ||
* Применить закрытый ключ для расшифрования сообщения: | * Применить закрытый ключ для расшифрования сообщения: | ||
| − | *: <tex>m = D(c) = c^d \mod n </tex> | + | *: <tex>m = D(c) = c^d \mod n ~~~~ (2)</tex> |
| + | |||
| + | ===Корректность схемы <tex>\mathtt{RSA}</tex>=== | ||
| + | {{Теорема | ||
| + | |statement=Уравнения <tex>(1)</tex> и <tex>(2)</tex>, на которых основана схема <tex>\mathtt{RSA}</tex>, определяют взаимно обратные преобразования множества <tex>\mathbb{Z}_n</tex> | ||
| + | |proof= | ||
| + | Действительно, для <math>\forall m \in \mathbb{Z}_{n}</math> | ||
| + | : <math>D\left( {E\left( m \right)} \right) = E\left( {D\left( m \right)} \right) = m^{ed} \mod n</math> | ||
| + | |||
| + | Покажем, что: | ||
| + | : <math>\forall m \in \mathbb{Z}_{n}: m^{ed} \equiv m \mod p</math>. | ||
| + | |||
| + | Возможны два случая: | ||
| + | * <math>m \not\equiv 0 \mod p</math>. | ||
| + | |||
| + | Поскольку числа <math>e</math> и <math>d</math> являются взаимно обратными относительно умножения по модулю <math>\varphi(n)=(p-1)(q-1)</math>, т.e | ||
| + | |||
| + | : <math>ed=1+k(p-1)(q-1)</math> для некоторого целого <math>k</math>, | ||
| + | |||
| + | тогда: | ||
| + | |||
| + | : <math>\begin{align} | ||
| + | m^{ed} & \equiv m^{1 + k\left( {p - 1} \right)\left( {q - 1} \right)} & \equiv & \mod p \\ | ||
| + | & \equiv m\left( {m^{p - 1} } \right)^{k\left( {q - 1} \right)} & \equiv & \mod p \\ | ||
| + | & \equiv m\left( 1 \right)^{k\left( {q - 1} \right)} & \equiv m & \mod p | ||
| + | \end{align}</math> | ||
| + | |||
| + | где второе тождество следует из [[Теорема_Ферма|теоремы Ферма]]. | ||
| + | |||
| + | * Рассмотрим второй случай: | ||
| + | : <math>m \equiv 0 \mod p</math>, | ||
| + | тогда | ||
| + | : <math>m^{ed} \equiv 0 \equiv m \mod p</math> | ||
| + | |||
| + | Таким образом, при всех <math>m</math> выполняется равенство | ||
| + | |||
| + | ::: <math>m^{ed} \equiv m \mod p</math> | ||
| + | |||
| + | Аналогично можно показать, что: | ||
| + | : <math>\forall m \in \mathbb{Z}_{n}: m^{ed} \equiv m \mod q</math>. | ||
| + | |||
| + | Тогда, из [[китайская теорема об остатках|китайской теоремы об остатках]] | ||
| + | : <math>\forall m \in \mathbb{Z}_{n}: m^{ed} \equiv m \mod n</math> | ||
| + | }} | ||
| + | |||
| + | ===Криптографическая стойкость=== | ||
==Применение== | ==Применение== | ||
Версия 02:43, 3 мая 2018
| Определение: |
| RSA (аббревиатура от фамилий Rivest, Shamir и Adleman) — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел. |
Криптосистема стала первой системой, пригодной и для шифрования, и для цифровой подписи.
Содержание
Реализация
Алгоритм включает в себя четыре этапа: генерация ключей, передача ключей, шифрование и расшифрование.
Криптографические системы с открытым ключом используют так называемые односторонние функции.
| Определение: |
| Односторонняя функция (англ. one-way function) — математическая функция, которая легко вычисляется для любого входного значения, но трудно найти аргумент по заданному значению функции. |
Под односторонностью понимается не теоретическая однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.
В основу криптографической системы с открытым ключом положена сложность задачи факторизации произведения двух больших простых чисел. Для шифрования используется операция возведения в степень по модулю большого числа. Для дешифрования (обратной операции) за разумное время необходимо уметь вычислять функцию Эйлера от данного большого числа, для чего необходимо знать разложение числа на простые множители.
| Определение: |
| Возведение в степень по модулю (англ. modular exponentiation) — это вычисление остатка от деления натурального числа (основание), возведенного в степень (показатель степени), на натуральное число (модуль). Обозначается: |
В криптографической системе с открытым ключом каждый участник располагает как открытым ключом (англ. public key), так и закрытым ключом (англ. private key). В криптографической системе каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их. Открытый и закрытый ключи каждого участника обмена сообщениями в криптосистеме образуют «согласованную пару» в том смысле, что они являются взаимно обратными. То есть для любых допустимых пар открытого и закрытого ключей существуют соответствующие функции шифрования и расшифрования такие, что для любого сообщения , где — множество допустимых сообщений,
Создание открытого и секретного ключей
-ключи генерируются следующим образом:
- Выбираются два различных случайных простых числа и заданного размера (например, бита каждое).
- Вычисляется их произведение , которое называется модулем.
- Вычисляется значение функции Эйлера от числа :
- Выбирается целое число (), взаимно простое со значением функции . Обычно в качестве берут простые числа, содержащие небольшое количество единичных бит в двоичной записи.
- Число называется открытой экспонентой (англ. public exponent)
- Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в .
- Слишком малые значения , например 3, потенциально могут ослабить безопасность схемы .
- Вычисляется число , мультипликативно обратное к числу по модулю , то есть число, удовлетворяющее сравнению:
- Число называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
- Пара публикуется в качестве открытого ключа (англ. public key).
- Пара играет роль закрытого ключа (англ. private key) и держится в секрете.
| Определение: |
| Случайное простое число (англ. random prime numbers) — в криптографии, простое число, содержащее в двоичной записи заданное количество битов |
Передача ключей
Предположим, что Боб хочет отправить Алисе информацию . Если они решат использовать , Боб должен знать открытый ключ Алисы для того чтобы зашифровать сообщение, а Алиса должна использовать свой закрытый ключ для расшифрования сообщения. Чтобы позволить Бобу отправлять свои зашифрованные сообщения, Алиса передает свой открытый ключ Бобу через надежный, но не обязательно секретный маршрут. Закрытый ключ Алисы никогда никому не передается.
Шифрование
Предположим, Боб хочет послать Алисе сообщение . Сообщениями являются целые числа в интервале от до , то есть . Алгоритм:
- Взять открытый ключ Алисы
- Взять открытый текст
- Зашифровать сообщение с использованием открытого ключа Алисы:
Расшифрование
Алгоритм:
- Принять зашифрованное сообщение
- Взять свой закрытый ключ
- Применить закрытый ключ для расшифрования сообщения:
Корректность схемы
| Теорема: |
Уравнения и , на которых основана схема , определяют взаимно обратные преобразования множества |
| Доказательство: |
|
Действительно, для Покажем, что:
Возможны два случая:
Поскольку числа и являются взаимно обратными относительно умножения по модулю , т.e
тогда: где второе тождество следует из теоремы Ферма.
тогда Таким образом, при всех выполняется равенство Аналогично можно показать, что:
Тогда, из китайской теоремы об остатках |
Криптографическая стойкость
Применение
Система используется для защиты программного обеспечения и в схемах цифровой подписи. Также она используется в открытой системе шифрования PGP и иных системах шифрования (к примеру, DarkCryptTC и формат xdc) в сочетании с симметричными алгоритмами.
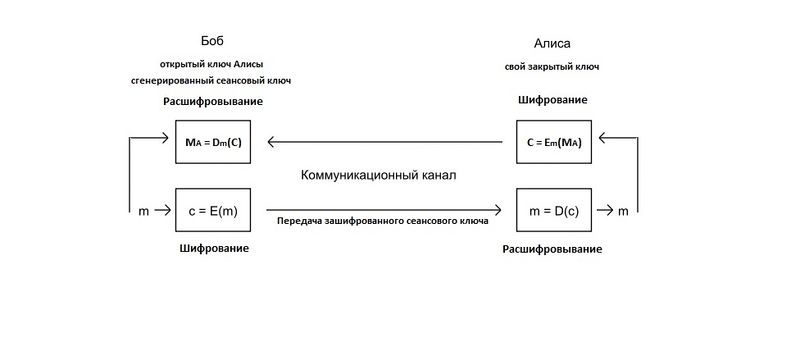
Наиболее используемым в настоящее время является смешанный алгоритм шифрования, в котором сначала шифруется сеансовый ключ, а потом уже с его помощью участники шифруют свои сообщения симметричными системами. После завершения сеанса сеансовый ключ, как правило, уничтожается.
Алгоритм шифрования сеансового ключа выглядит следующим образом:
Шифрование
Алгоритм:
- Взять открытый ключ Алисы
- Создать случайный сеансовый ключ
- Зашифровать сеансовый ключ с использованием открытого ключа Алисы:
- Расшифровать сообщение с помощью сеансового ключа симметричным алгоритмом:
Расшифрование
Алгоритм:
- Принять зашифрованный сеансовый ключ Боба
- Взять свой закрытый ключ
- Применить закрытый ключ для расшифровывания сеансового ключа:
- Зашифровать сообщение с помощью сеансового ключа симметричным алгоритмом:
Минусы
Алгоритм намного медленнее, чем AES и другие алгоритмы, использующие симметричные блочные шифры.
При неправильной или неоптимальной реализации или использовании алгоритма возможны специальные криптографические атаки, такие как атаки на схемы с малой секретной экспонентой или на схемы с общим выбранным значением модуля.
Из-за низкой скорости шифрования (около 30 кбит/с при 512 битном ключе на процессоре 2 ГГц), сообщения обычно шифруют с помощью более производительных симметричных алгоритмов со случайным сеансовым ключом (например, AES, IDEA, Serpent, Twofish), а с помощью шифруют лишь этот ключ, таким образом реализуется гибридная криптосистема.