Splay-дерево — различия между версиями
(→Splay) |
|||
| Строка 12: | Строка 12: | ||
[[file:zig.jpg|500px|Zig - поворот]] | [[file:zig.jpg|500px|Zig - поворот]] | ||
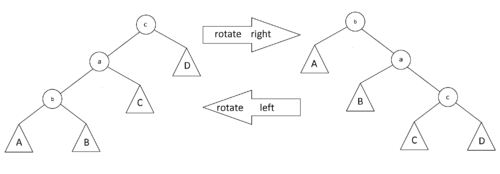
# Zig-Zig. Если <tex> p(x) </tex> - не корень дерева, а <tex> x </tex> и <tex> p(x) </tex> - оба левые или оба правые дети, то делаем поворот ребра <tex> \langle p(x), p(p(x)) \rangle </tex>, а затем поворот ребра <tex> \langle x, p(x) \rangle </tex>. | # Zig-Zig. Если <tex> p(x) </tex> - не корень дерева, а <tex> x </tex> и <tex> p(x) </tex> - оба левые или оба правые дети, то делаем поворот ребра <tex> \langle p(x), p(p(x)) \rangle </tex>, а затем поворот ребра <tex> \langle x, p(x) \rangle </tex>. | ||
| − | + | [[file:Zigzig.PNG|500px|Zig-zig - поворот]] | |
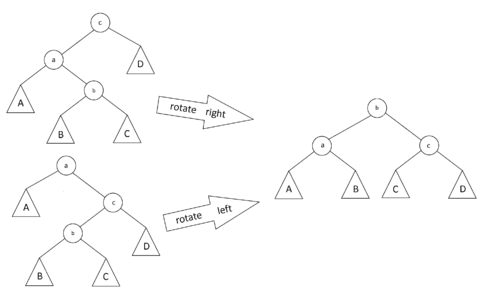
# Zig-Zag. Если <tex> p(x) </tex> - не корень дерева и <tex> x </tex> - левый ребенок, а <tex> p(x) </tex> - правый, или наоборот, то делаем поворот вокруг ребра <tex> \langle x, p(x) \rangle </tex>, а затем поворот нового ребра <tex> \langle x, p(x) \rangle </tex>, где <tex> p(x) </tex> - новый родитель <tex> x </tex>. | # Zig-Zag. Если <tex> p(x) </tex> - не корень дерева и <tex> x </tex> - левый ребенок, а <tex> p(x) </tex> - правый, или наоборот, то делаем поворот вокруг ребра <tex> \langle x, p(x) \rangle </tex>, а затем поворот нового ребра <tex> \langle x, p(x) \rangle </tex>, где <tex> p(x) </tex> - новый родитель <tex> x </tex>. | ||
| − | + | [[file:zigzag.PNG|500px|Zig-zag - поворот]] | |
Данная операция занимает <tex> O(d) </tex> времени, где <tex> d </tex> - длина пути от <tex> x </tex> до корня. В результате этой операции <tex> x </tex> становится корнем дерева, а расстояние до корня от каждой вершины сокращается примерно пополам, что связано с разделением случаев "zig-zig" и "zig-zag". | Данная операция занимает <tex> O(d) </tex> времени, где <tex> d </tex> - длина пути от <tex> x </tex> до корня. В результате этой операции <tex> x </tex> становится корнем дерева, а расстояние до корня от каждой вершины сокращается примерно пополам, что связано с разделением случаев "zig-zig" и "zig-zag". | ||
Версия 16:50, 30 июня 2011
Сплей-дерево (Splay-tree) — саморегулирующееся двоичное дерево поиска. Относится к разряду сливаемых деревьев. Сплей-дерево было придумано Робертом Тарьяном и Даниелем Слейтером в 1983 году.
Основной идей для сохранение баланса дерева является перетаскивание найденной вершины в корень после каждой операции поиска.
Содержание
Move to Root
Пусть - предок вершины . Эвристика "Move to Root" совершает повороты вокруг ребра , пока не окажется корнем дерева. Данный поворот аналогичен zig - повороту.
Splay
"Splay" так же как и "Move to Root" перетаскивает вершину в корень дерева, но при этом она использует другую последовательность поворотов. Пока не является корнем дерева выполняется следующее :
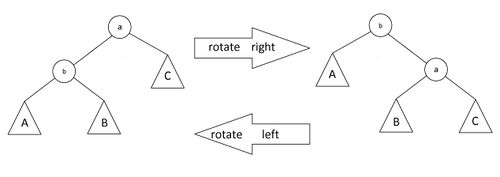
- Zig. Если - корень дерева, то совершаем один поворот вокруг ребра , делая корнем дерева. Данный случай является крайним и выполняется только один раз в конце, если изначальная глубина была нечетной.
- Zig-Zig. Если - не корень дерева, а и - оба левые или оба правые дети, то делаем поворот ребра , а затем поворот ребра .
- Zig-Zag. Если - не корень дерева и - левый ребенок, а - правый, или наоборот, то делаем поворот вокруг ребра , а затем поворот нового ребра , где - новый родитель .
Данная операция занимает времени, где - длина пути от до корня. В результате этой операции становится корнем дерева, а расстояние до корня от каждой вершины сокращается примерно пополам, что связано с разделением случаев "zig-zig" и "zig-zag".
Merge
Merge(, ). У нас есть два дерева и , причём подразумевается, что все элементы первого дерева меньше элементов второго. Запускаем Splay от самого большого элемента в дереве (пусть это элемент ). После этого корень содержит элемент , при этом у него нет правого ребёнка. Делаем правым поддеревом и возвращаем полученное дерево.
Split
Split(, ). Запускаем Splay от элемента и возвращаем два дерева, полученные отсечением правого или левого поддерева от корня, в зависимости от того, содержит корень элемент больше или не больше, чем .
Add
Add(, ). Запускаем Split(, ), который нам возвращает деревья и , их подвешиваем к как левое и правое поддеревья соответственно.
Remove
Remove(, ). Запускаем Splay от -го элемента и возвращаем Merge от его детей.
Анализ операции splay
Амортизационный анализ сплей-дерева проводится с помощью метода потенциалов. Потенциалом рассматриваемого дерева назовём сумму рангов его вершин. Ранг вершины — это величина, обозначаемая и равная , где — количество вершин в поддереве с корнем в .
| Лемма: |
Амортизированное время операции splay вершины в дереве с корнем не превосходит |
| Доказательство: |
|
Проанализируем каждый шаг операции splay. Пусть и — ранги вершин после шага и до него соответственно, — предок вершины , а — предок (если есть). Разберём случаи в зависимости от типа шага: Zig. Поскольку выполнен один поворот, то время амортизированное время выполнения шага (поскольку только у вершин и меняется ранг). Ранг вершины уменьшился, поэтому . Ранг вершины увеличился, поэтому . Следовательно, . Zig-zig. Выполнено два поворота, амортизированное время выполнения шага . Поскольку после поворотов поддерево с корнем в будет содержать все вершины, которые были в поддереве с корнем в (и только их), поэтому . Используя это равенство, получаем: , поскольку . Далее, так как , получаем, что . Мы утверждаем, что эта сумма не превосходит , то есть, что . Преобразуем полученное выражение следующим образом: . Из рисунка видно, что , значит, сумма выражений под логарифмами не превосходит единицы. Далее, рассмотрим сумму логарифмов . При произведение по неравенству между средними не превышает . А поскольку логарифм - функция возрастающая, то , что и является требуемым неравенством. Zig-zag. Выполнено два поворота, амортизированное время выполнения шага . Поскольку , то . Далее, так как , то . Мы утверждаем, что эта сумма не превосходит , то есть, что . Но, поскольку - аналогично доказанному ранее, что и требовалось доказать. Итого, получаем, что амортизированное время шага zig-zag не превосходит . Поскольку за время выполнения операции splay выполняется не более одного шага типа zig, то суммарное время не будет превосходить , поскольку утроенные ранги промежуточных вершин сокращаются (входят в сумму как с плюсом, так и с минусом). |
Литература
- Daniel Sleator, Robert Tarjan "A data structure for dynamic trees"