Предикат "левый поворот"

Эта статья находится в разработке!

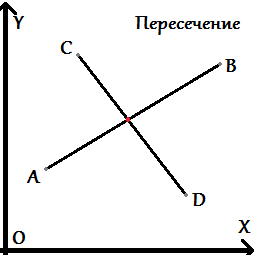
Допустим нам дана задача: Даны два отрезка AB и CD (они могут вырождаться в точки). Требуется проверить, пересекаются они на плоскости или нет. Для упрощения определения этого факта в вычислительной геометрии используется предикат "левый поворот" (или "по часовой стрелке"). Для начала разберемся, что за зверь такой - Предикат.

Определение:

Предикат (лат. praedicatum — заявленное, упомянутое, сказанное) — любое математическое высказывание, в котором есть, по меньшей мере, одна переменная

Примеры

- Например, обозначим предикатом EQ(x, y) отношение равенства («x = y»), где x и y принадлежат множеству вещественных чисел. В этом случае предикат EQ будет принимать истинное значение для всех равных x и y.

- Более житейским примером может служить предикат ПРОЖИВАЕТ(x, y, z) для отношения «x проживает в городе y на улице z» или ЛЮБИТ(x, y) для «x любит y».

Итак, у нас есть задача, с чего начнем её решать? Одно из решений - определить, лежат ли точки концов отрезков по разные стороны от другого отрезка. Вот тут нам и поможет наш предикат, где два из трех аргументов (например a и b) это точки концов одного отрезка, а последний - один из концов другого отрезка.

Определение:

Left_Turn(a, b, c) = true, если (b - a)*(c - a) > 0

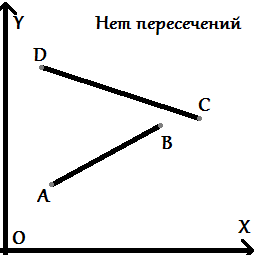
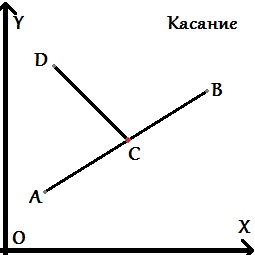
Какие могут быть расположения точек и самих отрезков относительно друг друга?

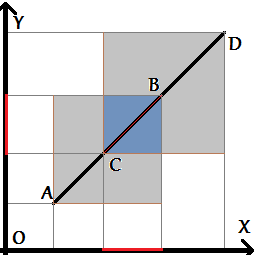
Единственное, на что следует обратить внимание — граничные случаи, когда какие-то точки попадают на саму прямую. При этом возникает единственный особый случай, когда вышеописанные проверки ничего не дадут — случай, когда оба отрезка лежат на одной прямой. Этот случай надо рассмотреть отдельно. Для этого достаточно проверить, что проекции этих двух отрезков на оси X и Y пересекаются (часто эту проверку называют "проверкой на bounding box").

Ссылки

• wikipedia.ru - Предикат
• e-maxx.ru/algo - Проверка двух отрезков на пересечение