Расстояние Хэмминга

Определение:

Расстояние Хэмминга (Hamming distance) — число позиций, в которых соответствующие цифры двух двоичных слов одинаковой длины различны. В более общем случае расстояние Хэмминга применяется для строк одинаковой длины любых k-ичных алфавитов и служит метрикой различия (функцией, определяющей расстояние в метрическом пространстве) объектов одинаковой размерности.

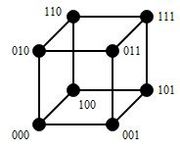
3-битный бинарный куб для нахождения расстояния Хэмминга

Пример

• [math]d(10{\color{Blue}1}1{\color{Blue}1}01, 10{\color{Red}0}1{\color{Red}0}01)=2[/math]
• [math]d(15{\color{Blue}38}1{\color{Blue}24}, 15{\color{Red}23}1{\color{Red}56})=4[/math]
• [math]d(h{\color{Blue}i}ll, h{\color{Red}o}ll)=1[/math]

Свойства

Расстояние Хэмминга обладает свойствами метрики, удовлетворяя следующим условиям:

• [math]~d(x, y) = 0 \iff x = y[/math]

• [math]~d(x,y)=d(y,x)[/math]

Объект x удален от объекта y так же, как объект y удален от объекта x.

• [math]~d(x,z) \le d(x,y) + d(y,z)[/math]

Третье свойство говорит, что дорога через третий объект с всегда длиннее, нежели прямой путь. Его обычно называют неравенством треугольника за его естественную геометрическую аналогию: сумма двух сторон треугольника всегда больше третьей стороны.

Доказательство: Пусть слова x и y отличаются в некоторой позиции t. Тогда какое бы слово z мы ни взяли, оно в этой позиции будет отличаться по крайней мере от одного из слов x и y. Следовательно, суммируя в правой части [math]~d(x, z)[/math] и [math]~d(z, y)[/math], мы обязательно учтем все позиции, в которых различались слова x и y.

Математики договорились любую функцию, обладающую указанными тремя свойствами, называть расстоянием.

См. также

Избыточное кодирование, код Хэмминга

Ссылки

• Расстояние Хэмминга — Википедия
• Hamming distance - Wikipedia