Теорема Менгера — различия между версиями
| Строка 1: | Строка 1: | ||
| − | |||
Теорема Менгера представляет собой группу теорем, связывающих такие понятия на графах как ''k-связность'' и ''количество непересекающихся путей'' относительно двух выделенных вершин. Возникают различные варианты очень похожих друг на друга по формулировке теорем в зависимости от того, рассматриваем ли мы ситуацию в ''ориентированном'' или ''неориентированном'' графе, и подразумеваем ли ''реберную k-связность'' и ''реберно непересекающиеся пути'' или же ''вершинную k-связность'' и ''вершинно непересекающиеся пути''. | Теорема Менгера представляет собой группу теорем, связывающих такие понятия на графах как ''k-связность'' и ''количество непересекающихся путей'' относительно двух выделенных вершин. Возникают различные варианты очень похожих друг на друга по формулировке теорем в зависимости от того, рассматриваем ли мы ситуацию в ''ориентированном'' или ''неориентированном'' графе, и подразумеваем ли ''реберную k-связность'' и ''реберно непересекающиеся пути'' или же ''вершинную k-связность'' и ''вершинно непересекающиеся пути''. | ||
| Строка 25: | Строка 24: | ||
|statement=Если в сети, где все пропускные способности ребер равны 1, существует целочисленный поток величиной <tex>L</tex> то существует и <tex>L</tex> реберно непересекающихся путей. | |statement=Если в сети, где все пропускные способности ребер равны 1, существует целочисленный поток величиной <tex>L</tex> то существует и <tex>L</tex> реберно непересекающихся путей. | ||
|proof= | |proof= | ||
| − | :В начале поймем, что если поток не нулевой, то существует маршрут из <tex>u</tex> в <tex>v</tex> лежащий только на ребрах с потоком равным 1. | + | :В начале поймем, что если поток не нулевой, то существует маршрут из <tex>u</tex> в <tex>v</tex> лежащий только на ребрах с потоком равным 1. В самом деле, если бы такого маршрута не существовало, то можно было бы выделить множество вершин до которых такие маршруты существуют, не включающее <tex>u</tex>, и по нему построить разрез. Поток через такой разрез, очевидно равен нулю, противоречие (<tex>f(S,T)=|f|</tex>, смотри [[Разрез, лемма о потоке через разрез|первую лемму]]). |
| − | |||
:Итак, найдем какой-нибудь маршрут из <tex>u</tex> в <tex>v</tex> лежащий только на ребрах где поток равен 1. Удалив все ребра находящиеся в этом маршруте и оставив все остальное неизменным, придем к целочисленному потоку величиной <tex>L-1</tex>. Ясно, что можно повторить тоже самое еще <tex>L-1</tex> раз, и, таким образом мы выделим <tex>L</tex> реберно непересекающихся маршрутов. | :Итак, найдем какой-нибудь маршрут из <tex>u</tex> в <tex>v</tex> лежащий только на ребрах где поток равен 1. Удалив все ребра находящиеся в этом маршруте и оставив все остальное неизменным, придем к целочисленному потоку величиной <tex>L-1</tex>. Ясно, что можно повторить тоже самое еще <tex>L-1</tex> раз, и, таким образом мы выделим <tex>L</tex> реберно непересекающихся маршрутов. | ||
| Строка 51: | Строка 49: | ||
|statement=Между вершинами <tex>u</tex> и <tex>v\; \exists L</tex> вершинно непересекающихся путей <tex>\Leftrightarrow</tex> после удаления <tex>\forall L-1</tex> вершин <tex>\exists</tex> путь из <tex>u</tex> в <tex>v</tex>. | |statement=Между вершинами <tex>u</tex> и <tex>v\; \exists L</tex> вершинно непересекающихся путей <tex>\Leftrightarrow</tex> после удаления <tex>\forall L-1</tex> вершин <tex>\exists</tex> путь из <tex>u</tex> в <tex>v</tex>. | ||
|proof= | |proof= | ||
| − | + | ||
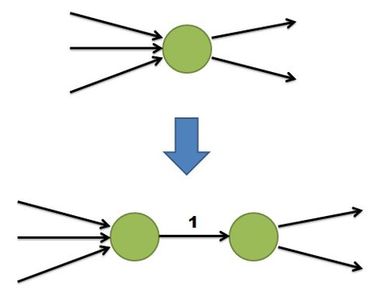
| − | + | :Разобьем каждую вершину на две таким образом: | |
| − | + | ||
| + | :[[Файл:Menger-vertex.JPG]] | ||
| + | |||
| + | :''(все входящие ребра заходят в правую вершину, выходящие - из левой. между двумя новыми вершинами добавляем ребро)'' | ||
| + | |||
| + | :Теперь задача практически сведена к первой теореме. | ||
| + | :Необходимо лишь отметить, что если в старом графе пути вершинно пересекаются, то в новом графе пути необходимо реберно пересекаются и наоборот. | ||
| + | :Кроме того, предложение "удалить в исходном графе <tex>\forall L</tex> вершин" превращается "в новом графе можно удалить <tex>\forall L</tex> ребер" (достаточно выбирать вершины на концах этих ребер). Можно преобразовывать и обратно, если удалять ребра между парой вершин, которые раньше были одним целым. | ||
}} | }} | ||
| + | <includeonly> | ||
| + | Теоремы для неореинтированного графа формулируются идентично, а их докозательства сводятся к своим ориентированным двойникам путем замены каждого ребра на две дуги: | ||
| − | + | [[Файл:Menger_undirected.JPG]] | |
| − | / | + | </includeonly> |
| − | |||
==Смотри также== | ==Смотри также== | ||
*[[Теорема Менгера, альтернативное доказательство]] | *[[Теорема Менгера, альтернативное доказательство]] | ||
Версия 07:23, 27 октября 2011
Теорема Менгера представляет собой группу теорем, связывающих такие понятия на графах как k-связность и количество непересекающихся путей относительно двух выделенных вершин. Возникают различные варианты очень похожих друг на друга по формулировке теорем в зависимости от того, рассматриваем ли мы ситуацию в ориентированном или неориентированном графе, и подразумеваем ли реберную k-связность и реберно непересекающиеся пути или же вершинную k-связность и вершинно непересекающиеся пути.
Подготовка к доказательству
Для доказательства мы будем пользоваться развитой раннее теорией потоков. Кроме базовых определений нам потребуется понятие остаточной сети (иначе - дополнительной сети), а также теорема Форда-Фалкерсона.
Кроме того потребуется лемма о целочисленности потока, которую сейчас и докажем:
| Лемма (о целочисленности потока): |
Если пропускные способности всех ребер целочисленные (сеть целочислена), то существует максимальный поток, целочисленный на каждом ребре. |
| Доказательство: |
|
И, наконец, сделаем немного более осознаным в общем-то и так интуитивно-понятное утверждение:
| Утверждение: |
Если в сети, где все пропускные способности ребер равны 1, существует целочисленный поток величиной то существует и реберно непересекающихся путей. |
|
Теорема
Теперь сама теорема будет тривиальным следствием. В начале сформулируем и докажем реберную версию для случая ориентированного графа.
| Теорема (Менгера о реберной двойственности в ориентированном графе): |
Между вершинами и реберно непересекающихся путей после удаления ребер путь из в . |
| Доказательство: |
|
| Теорема (Менгера о вершинной двойственности в ориентированном графе): |
Между вершинами и вершинно непересекающихся путей после удаления вершин путь из в . |
| Доказательство: |
|
Смотри также
Литература
- Ловас Л., Пламмер М. Прикладные задачи теории графов. Теория паросочетаний в математике, физике, химии 1998. 656 с. ISBN 5-03-002517-0 (глава 2.4 стр. 117)